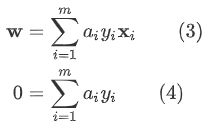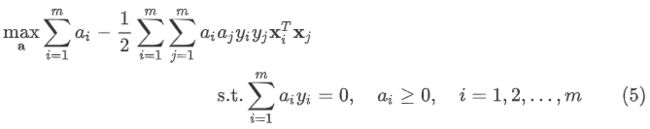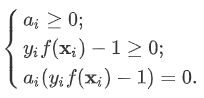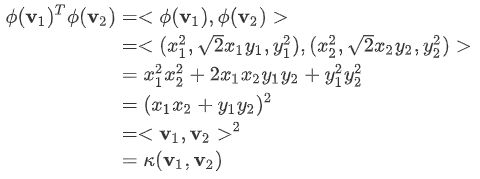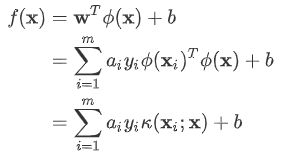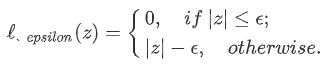《机器学习》周志华西瓜书学习笔记(六):支持向量机
【机器学习】《机器学习》周志华西瓜书 笔记/习题答案 总目录
- https://blog.csdn.net/TeFuirnever/article/details/96178919
——————————————————————————————————————————————————————
- 【机器学习】《机器学习》周志华西瓜书习题参考答案:第6章 - 支持向量机
- 【机器学习】《机器学习实战》读书笔记及代码:第6章 - 支持向量机
支持向量机
支持向量机(Support Vector Machine,简称SVM)是一种针对二分类任务设计的分类器,它的理论相对神经网络模型来说更加完备和严密,并且效果显著,结果可预测,是非常值得学习的模型。
这一章的内容大致如下:
-
间隔与支持向量:如何计算空间中任一点到超平面的距离?什么是支持向量?什么是间隔?支持向量机求解的目标是什么?
-
对偶问题:求取最大间隔等价于怎样的对偶问题?KKT条件揭示出支持向量机的什么性质?如何用SMO算法进行高效求解?为什么SMO算法能高效求解?
-
核函数:如何处理非线性可分问题?什么是核函数?为什么需要核函数?有哪些常用的核函数?核函数具有什么性质?
-
软间隔与正则化:如何应对过拟合问题?软间隔和硬间隔分别指什么?如何求解软间隔支持向量机?0/1损失函数有哪些可选的替代损失函数?支持向量机和对率回归模型有什么联系?结构风险和经验风险分别指什么?
-
支持向量回归:什么是支持向量回归?与传统回归模型有什么不同?支持向量回归的支持向量满足什么条件?
-
核方法:什么是表示定理?什么是核方法?如何应用?
间隔与支持向量
给定一个二分类数据集,正类标记为+1,负类标记为-1(对率回归中负类标记是0,这点是不同的)。
分类学习最基本的想法就是基于训练、集D 在样本空间中找到一个划分超平面、将不同类别的样本分开但能将训练样本分开的划分超平面可能有很多,哪一个才是最好的呢?

支持向量
在SVM中,我们试图找到 处于两类样本正中间的划分超平面,因为该划分超平面 对训练数据局部扰动的容忍性最好。换言之,这个划分超平面所产生的分类结果是 最鲁棒的,对未见示例的 泛化能力最强。
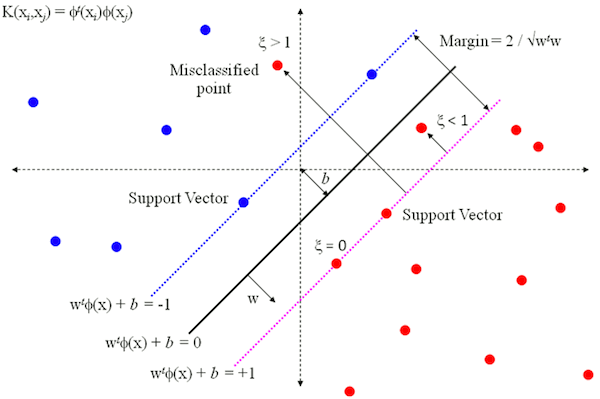
上图的黑色实线就是划分超平面,在线性模型中可以通过线性方程 w T x + b = 0 \mathbf{w}^T\mathbf{x}+b=0 wTx+b=0 来描述,在二维样本空间中就是一条直线。图中的 ϕ ( x ) \phi(\mathbf{x}) ϕ(x) 是使用了核函数进行映射,这里先不讨论。 w \mathbf{w} w 是线性模型的权重向量(又叫 投影向量),也是 划分超平面的法向量,决定着超平面的方向。偏置项 b b b 又被称为 位移项,决定了超平面和空间原点之间的距离。
假设超平面能够将所有训练样本正确分类,也即对于所有标记为 +1 的点有 w T x + b > 0 \mathbf{w}^T\mathbf{x}+b>0 wTx+b>0,所有标记为 -1 的点有 w T x + b < 0 \mathbf{w}^T\mathbf{x}+b<0 wTx+b<0。只要这个超平面存在,那么我们必然可以对 w \mathbf{w} w 和 b b b 进行适当的 线性放缩,使得:
w T x + b ≥ + 1 , y i = + 1 \mathbf{w}^T\mathbf{x}+b\geq+1,\quad y_i = +1 wTx+b≥+1,yi=+1
w T x + b ≤ − 1 , y i = − 1 \mathbf{w}^T\mathbf{x}+b\leq-1,\quad y_i = -1 wTx+b≤−1,yi=−1
而SVM中定义 使得上式等号成立的训练样本点 就是 支持向量(support vector)(如果叫作 支持点 可能更好理解一些,因为事实上就是样本空间中的数据点,但因为在表示数据点的时候一般写成向量形式,所以就称为 支持向量),它们是距离超平面最近的几个样本点,也即上面图中两条虚线上的点(图中存在比支持向量距离超平面更近的点,这跟 软间隔 有关,这里先不讨论)。
在SVM中,我们希望实现的是 最大化两类支持向量到超平面的距离之和。
源自 https://github.com/familyld/Machine_Learning 的解释
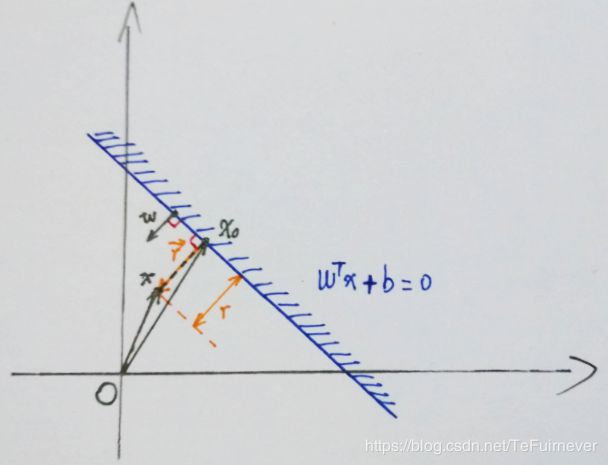
那首先就得知道怎么计算距离,怎样计算样本空间中任意数据点到划分超平面的距离 呢?
画了一个图,方便讲解。图中蓝色线即超平面,对应直线方程 w T x + b = 0 \mathbf{w}^T\mathbf{x}+b=0 wTx+b=0。投影向量 w \mathbf{w} w垂直于超平面,点 x x x 对应向量 x \mathbf{x} x,过点 x x x 作超平面的垂线,交点 x 0 x_0 x0 对应向量 x 0 \mathbf{x_0} x0。假设 由点 x 0 x_0 x0 指向点 x x x 的向量 为 r \mathbf{r} r,长度(也即点 x x x 与超平面的距离)为 r r r。
有两种方法计算可以计算出 r r r 的大小:
方法1:向量计算
由向量加法定义可得 x = x 0 + r \mathbf{x} = \mathbf{x_0} + \mathbf{r} x=x0+r
那么向量 r \mathbf{r} r 等于什么呢?它等于这个方向的单位向量乘上 r r r,也即有 r = w ∥ w ∥ ⋅ r \mathbf{r} = \frac{\mathbf{w}}{\Vert \mathbf{w} \Vert} \cdot r r=∥w∥w⋅r
因此又有 x = x 0 + w ∥ w ∥ ⋅ r \mathbf{x} = \mathbf{x_0} + \frac{\mathbf{w}}{\Vert \mathbf{w} \Vert} \cdot r x=x0+∥w∥w⋅r
由于点 x 0 x_0 x0 在超平面上,所以有 w T x 0 + b = 0 \mathbf{w}^T\mathbf{x_0}+b=0 wTx0+b=0
由 x = x 0 + w ∥ w ∥ ⋅ r \mathbf{x} = \mathbf{x_0} + \frac{\mathbf{w}}{\Vert \mathbf{w} \Vert} \cdot r x=x0+∥w∥w⋅r 可得 x 0 = x − w ∥ w ∥ ⋅ r \mathbf{x_0} = \mathbf{x} - \frac{\mathbf{w}}{\Vert \mathbf{w} \Vert} \cdot r x0=x−∥w∥w⋅r,代入直线方程消去 x 0 \mathbf{x_0} x0:
w T x 0 + b = w T ( x − w ∥ w ∥ ⋅ r ) + b = 0 \mathbf{w}^T\mathbf{x_0}+b = \mathbf{w}^T(\mathbf{x} - \frac{\mathbf{w}}{\Vert \mathbf{w} \Vert} \cdot r)+b = 0 wTx0+b=wT(x−∥w∥w⋅r)+b=0
简单变换即可得到:
r = w T x + b ∥ w ∥ r = \frac{\mathbf{w}^T\mathbf{x}+b}{\Vert \mathbf{w} \Vert} r=∥w∥wTx+b
又因为我们取距离为正值,所以要加上绝对值符号:
r = ∣ w T x + b ∣ ∥ w ∥ r = \frac{|\mathbf{w}^T\mathbf{x}+b|}{\Vert \mathbf{w} \Vert} r=∥w∥∣wTx+b∣
方法2:点到直线距离公式
假设直线方程为 a x 1 + b x 2 + c = 0 ax_1 + bx_2 + c= 0 ax1+bx2+c=0,那么有点到直线距离公式:
r = ∣ a x + b x 2 + c ∣ a 2 + b 2 r = \frac{|ax + bx_2 + c|}{\sqrt{a^2+b^2}} r=a2+b2∣ax+bx2+c∣
令 w = ( a , b ) \mathbf{w} = (a,b) w=(a,b), x = ( x 1 , x 2 ) \mathbf{x} = (x_1,x_2) x=(x1,x2),则可以把 a x 1 + b x 2 ax_1 + bx_2 ax1+bx2 写成向量形式 w T x \mathbf{w}^T\mathbf{x} wTx。把截距项设为 b b b,则直线方程变为 w T x + b = 0 \mathbf{w}^T\mathbf{x}+b=0 wTx+b=0,代入距离公式可得:
r = ∣ w T x + b ∣ w T w = ∣ w T x + b ∣ ∥ w ∥ r = \frac{|\mathbf{w}^T\mathbf{x}+b|}{\sqrt{\mathbf{w}^T\mathbf{w}}} = \frac{|\mathbf{w}^T\mathbf{x}+b|}{\Vert \mathbf{w} \Vert} r=wTw∣wTx+b∣=∥w∥∣wTx+b∣
该式扩展到多维情况下也是通用的。
间隔
前面已经提到,希望实现的是 最大化两类支持向量到超平面的距离之和,而根据定义,所有支持向量都满足:
w T x + b = + 1 , y i = + 1 \mathbf{w}^T\mathbf{x}+b = +1,\quad y_i = +1 wTx+b=+1,yi=+1
w T x + b = − 1 , y i = − 1 \mathbf{w}^T\mathbf{x}+b = -1,\quad y_i = -1 wTx+b=−1,yi=−1
代入前面的距离公式,
r = ∣ w T x + b ∣ ∥ w ∥ r = \frac{|\mathbf{w}^T\mathbf{x}+b|}{\Vert \mathbf{w} \Vert} r=∥w∥∣wTx+b∣
可以得到支持向量到超平面的距离为 1 ∥ w ∥ \frac{1}{\Vert \mathbf{w} \Vert} ∥w∥1。
定义 间隔(margin)为 两个异类支持向量到超平面的距离之和:
γ = 2 ⋅ 1 ∥ w ∥ = 2 ∥ w ∥ \gamma = 2 \cdot \frac{1}{\Vert \mathbf{w} \Vert} = \frac{2}{\Vert \mathbf{w} \Vert} γ=2⋅∥w∥1=∥w∥2
SVM的目标便是找到 具有最大间隔(maximum margin) 的划分超平面,也即找到使 γ \gamma γ 最大的参数 w \mathbf{w} w 和 b b b:
max w , b 2 ∥ w ∥ s . t . y i ( w T x + b ) ≥ 1 , i = 1 , 2 , . . . , m \max_{\mathbf{w},b} \frac{2}{\Vert \mathbf{w} \Vert} \quad s.t. \quad y_i(\mathbf{w}^T\mathbf{x}+b) \geq 1, \quad i=1,2,...,m w,bmax∥w∥2s.t.yi(wTx+b)≥1,i=1,2,...,m
约束部分指的是全部样本都被正确分类,此时标记值( + 1 +1 +1 或 − 1 -1 −1)乘上预测值( ≥ + 1 \geq +1 ≥+1 或 ≤ − 1 \leq -1 ≤−1)必定是一个 ≥ 1 \geq 1 ≥1 的数值。看上去间隔大小只与 w \mathbf{w} w 有关,但实际上位移项 b b b 也通过约束影响着 w \mathbf{w} w 的取值,进而对间隔产生影响。
由于最大化 ∥ w ∥ − 1 \Vert \mathbf{w} \Vert^{-1} ∥w∥−1 等价于最小化 ∥ w ∥ 2 \Vert \mathbf{w} \Vert^{2} ∥w∥2,所以可以重写 目标函数 为:
min w , b 1 2 ∥ w ∥ 2 s . t . y i ( w T x + b ) ≥ 1 , i = 1 , 2 , . . . , m ( 1 ) \min_{\mathbf{w},b} \frac{1}{2} \Vert \mathbf{w} \Vert^2 \quad s.t. \quad y_i(\mathbf{w}^T\mathbf{x}+b) \geq 1, \quad i=1,2,...,m\qquad(1) w,bmin21∥w∥2s.t.yi(wTx+b)≥1,i=1,2,...,m(1)
引入 1 2 \frac{1}{2} 21 是为了求导时可以约去平方项的2,这便是 支持向量机的基本型。
特别地,还有以下定义:
-
函数间隔: y i ( w T x + b ) y_i(\mathbf{w}^T\mathbf{x}+b) yi(wTx+b)
-
几何间隔: y i ( w T x + b ) ∥ w ∥ 2 \frac{y_i(\mathbf{w}^T\mathbf{x}+b)}{\Vert \mathbf{w} \Vert^2} ∥w∥2yi(wTx+b)
对偶问题
式(1)是一个 带约束的凸二次规划(convex quadratic programming)问题(凸问题就意味着必定能求到全局最优解,而不会陷入局部最优)。对这样一个问题,可以直接用现成的优化计算包求解,但这一小节介绍的是一种更高效的方法。
首先为式(1)的每条约束添加拉格朗日乘子 a i ≥ 0 a_i \geq 0 ai≥0(对应m个样本的m条约束),得到该问题的拉格朗日函数:
L ( w , b , a ) = 1 2 ∥ w ∥ 2 + ∑ i = 1 m a i ( 1 − y i ( w T x i + b ) ) ( 2 ) L(\mathbf{w},b,\mathbf{a}) = \frac{1}{2} \Vert \mathbf{w} \Vert^2 + \sum_{i=1}^m a_i(1-y_i(\mathbf{w}^T\mathbf{x}_i+b))\qquad(2) L(w,b,a)=21∥w∥2+i=1∑mai(1−yi(wTxi+b))(2)
其中 a = ( a 1 ; a 2 ; . . . ; a m ) \mathbf{a} = (a_1;a_2;...;a_m) a=(a1;a2;...;am),对拉格朗日函数求 w \mathbf{w} w 和 b b b 的偏导,并令偏导为0可以得到:
将式(3)代入式(2)可以消去 w \mathbf{w} w,又因为式(2)中 b b b 的系数是 a i y i a_i y_i aiyi,由式(4)可知 b b b 也可以消去。然后再考虑式(4)的约束就得到了式(1)的 对偶问题(dual problem):
只要求出该对偶问题的解 a \mathbf{a} a,就可以推出 w \mathbf{w} w 和 b b b,从而得到模型:
不过实际计算时一般不会直接求解 a \mathbf{a} a,特别是需要用核函数映射到高维空间时,因为映射后做内积很困难,而用少量支持向量进行表示,在原始空间进行计算显然更优,这点在后续章节会详细讲解。
注意,由于式(1)的约束条件是 不等式约束,所以求解过程要求满足 KKT(Karush-Kuhn-Tucker)条件:
这个 KKT条件 说明了,对任何一个样本 x i \mathbf{x}_i xi 来说,
-
要么对应的拉格朗日乘子 a i a_i ai 为0,此时样本 x i \mathbf{x}_i xi 对式(6)毫无贡献,将不会在式(6)求和中出现,不会影响到模型,也就不会对 f ( x ) f(x) f(x) 有任何影响;
-
要么 a i > 0 a_i > 0 ai>0,则必有函数间隔 y i f ( x i ) = 1 y_i f(\mathbf{x}_i) = 1 yif(xi)=1,此时所对应的样本点 x i \mathbf{x}_i xi 位于最大间隔边界上,是一个支持向量。
它揭示了SVM的一个重要性质:训练完成后,大部分的训练样本都不需保留,最终模型仅与支持向量有关。
SMO算法
可以发现对偶问题式(5)是一个二次规划问题,可以使用通用的二次规划算法求解。但 问题的规模正比于训练样本数,因此这会在实际任务中造成很大的开销。为了避免这个障碍,人们通过利用问题本身的特性,提出了很多高效算法,可以使用高效的 SMO(Sequential Minimal Optimization)算法。
SMO的基本思路是先固定向之外的所有参数,然后求向上的极值。由于存在约束:
![]()
若固定 a i a_i ai 之外的其他变量,则 a i a_i ai 可由其他变量导出。于是, SMO 每次选择两个变量 a i a_i ai 和 a j a_j aj,并固定其他参数。这样初始化参数 a \mathbf{a} a 后,SMO算法重复下面两个步骤直至收敛:
-
选取一对需要更新的变量 a i a_i ai 和 a j a_j aj
-
固定 a i a_i ai 和 a j a_j aj 以外的参数,求解对偶问题式(5)来更新 a i a_i ai 和 a j a_j aj
那么问题来了,怎么选取 a i a_i ai 和 a j a_j aj 呢?
注意到,只要选取的 a i a_i ai 和 a j a_j aj 中有一个不满足KKT条件,那么更新后目标函数的值就会增大。而且 违背KKT条件的程度越大,则更新后导致目标函数增幅就越大。因此,SMO算法 先选取一个违背KKT条件程度最大的变量 a i a_i ai,然后再选一个使目标函数增长最快的变量 a j a_j aj,但由于找出 a j a_j aj 的开销较大,所以SMO算法采用了一个 启发式,使 选取的两变量对应的样本之间间隔最大。这样两个变量差别很大,与选取两个相似变量相比,这种方法能为目标函数带来更大的变化,从而更快搜索到全局最大值。
由于SMO算法在每次迭代中,仅优化两个选定的参数,其他参数是固定的,所以会非常高效。此时,可将对偶问题式(5)的约束重写为:
a i y i + a j y j = c , a i ≥ 0 , a j ≥ 0 ( 7 ) a_iy_i + a_jy_j = c,\quad a_i \geq 0, a_j \geq 0 \qquad (7) aiyi+ajyj=c,ai≥0,aj≥0(7)
其中, c = − ∑ k ≠ i , j a k y k c = -\sum_{k \neq i,j} a_k y_k c=−∑k̸=i,jakyk 看作是固定的常数。
利用式(7),我们可以把 a j a_j aj 从式(5)中消去,这样就得到了一个 单变量二次规划问题,只需考虑 a i ≥ 0 a_i \geq 0 ai≥0 这个约束。这样的问题具有 闭式解,所以我们连数值优化方法都不需要了,可以直接算出 a i a_i ai 和 a j a_j aj。
使用SMO算法计算出最优解之后,我们关注的是如何推出 w \mathbf{w} w 和 b b b,从而得到最终模型。获得 w \mathbf{w} w 很简单,直接用式(3)就可以了。而位移项 b b b 则可以通过支持向量导出,因为对于任一支持向量 ( x s , y s ) (\mathbf{x}_s, y_s) (xs,ys),都有函数间隔等于1,所以有:
y s f ( x ) = y s ( ∑ i ∈ S a i y i x i T x s + b ) = 1 ( 8 ) y_sf(\mathbf{x}) = y_s(\sum_{i \in S} a_i y_i \mathbf{x}_i^T \mathbf{x}_s + b)= 1 \qquad (8) ysf(x)=ys(i∈S∑aiyixiTxs+b)=1(8)
这里的 S S S 是所有支持向量的下标集(事实上,用所有样本的下标也行,不过非支持向量的拉格朗日乘子等于0,对求和没贡献,这一点前面已经提到了)。
理论上,我们只要选取任意一个支持向量代入式(8)就可以把 b b b 算出来了。但实际任务中往往采用一种更鲁棒的做法:用所有支持向量求解的平均值。
b = 1 ∣ S ∣ ∑ s ∈ S ( 1 y s − ∑ i ∈ S a i y i x i T x s ) b = \frac{1}{|S|} \sum_{s \in S} (\frac{1}{y_s} - \sum_{i \in S}a_i y_i \mathbf{x}_i^T \mathbf{x}_s) b=∣S∣1s∈S∑(ys1−i∈S∑aiyixiTxs)
核函数
如何处理非线性划分
在现实任务中,我们更常遇到的是 在原始样本空间中非线性可分 的问题。对这样的问题,一种常用的思路是将样本从原始空间映射到一个更高维的特征空间,使得样本在该特征空间中线性可分。幸运的是,只要原始空间是有限维的(也即属性数目有限),那就必然存在一个高维特征空间使样本线性可分。
举个例子,二维平面上若干样本点呈如下左面的分布:
此时要划分两类样本,需要一个非线性的圆型曲线。假设原始空间中两个属性是 x x x 和 y y y,如果我们做一个映射,把样本点都映射到一个三维特征空间,维度取值分别为 x 2 x^2 x2, y 2 y^2 y2 和 y y y,则得到右面的分布。可以看到这个时候,我们只需要一个线性超平面就可以将两类样本完全分开了,也就是说可以用前面的方法来求解了。
什么是核函数
在上面的例子中,我们是把每个样本对应的二维的特征向量 x \mathbf{x} x 映射为一个三维的特征向量,假设我们 用 ϕ ( x ) \phi(\mathbf{x}) ϕ(x) 来表示映射所得的特征向量。则 在映射的高维特征空间中,用于划分的线性超平面可以表示为:
f ( x ) = w T ϕ ( x ) + b f(\mathbf{x}) = \mathbf{w}^T \phi(\mathbf{x}) + b f(x)=wTϕ(x)+b
类似式(1),可以得到此时的目标函数为:
min w , b 1 2 ∥ w ∥ 2 s . t . y i ( w T ϕ ( x ) + b ) ≥ 1 , i = 1 , 2 , . . . , m ( 9 ) \min_{\mathbf{w},b} \frac{1}{2} \Vert \mathbf{w} \Vert^2 \quad s.t. \quad y_i(\mathbf{w}^T\phi(\mathbf{x})+b) \geq 1, \quad i=1,2,...,m\qquad(9) w,bmin21∥w∥2s.t.yi(wTϕ(x)+b)≥1,i=1,2,...,m(9)
对应的对偶问题为:
max a ∑ i = 1 m a i − 1 2 ∑ i = 1 m ∑ j = 1 m a i a j y i y j ϕ ( x i ) T ϕ ( x j ) s . t . ∑ i = 1 m a i y i = 0 , a i ≥ 0 , i = 1 , 2 , . . . , m ( 10 ) \max_{\mathbf{a}} \sum_{i=1}^m a_i - \frac{1}{2} \sum_{i=1}^m\sum_{j=1}^m a_i a_j y_i y_j \phi(\mathbf{x}_i)^T \phi(\mathbf{x}_j) \quad s.t. \quad \sum_{i=1}^m a_i y_i = 0, \quad a_i \geq 0, \quad i=1,2,...,m \qquad (10) amaxi=1∑mai−21i=1∑mj=1∑maiajyiyjϕ(xi)Tϕ(xj)s.t.i=1∑maiyi=0,ai≥0,i=1,2,...,m(10)
注意到对偶问题中,涉及到 ϕ ( x i ) T ϕ ( x j ) \phi(\mathbf{x}_i)^T \phi(\mathbf{x}_j) ϕ(xi)Tϕ(xj) 的计算,也即 x i x_i xi 和 x j x_j xj 映射到高维特征空间后的内积(比如 x i = ( 1 , 2 , 3 ) x_i = (1,2,3) xi=(1,2,3), x j = ( 4 , 5 , 6 ) x_j = (4,5,6) xj=(4,5,6),那么内积 x i T x j x_i^Tx_j xiTxj 就等于 1 ∗ 4 + 2 ∗ 5 + 3 ∗ 6 = 32 1*4+2*5+3*6=32 1∗4+2∗5+3∗6=32),由于 特征空间维数可能很高,甚至可能是无穷维,所以 直接计算映射后特征向量的内积是很困难的。为了解决这样的问题,就引入了核函数(kernel function):
![]()
打个比方,假设输入空间是二维的,每个样本点有两个属性 x x x 和 y y y,存在映射将每个样本点映射到三维空间:
ϕ ( x ) = ϕ ( x , y ) = ( x 2 , 2 x y , y 2 ) \phi(\mathbf{x}) = \phi(x, y) = (x^2, \sqrt{2}xy, y^2) ϕ(x)=ϕ(x,y)=(x2,2xy,y2)
给定原始空间中的两个样本点 v 1 = ( x 1 , y 1 ) \mathbf{v}_1=(x_1,y_1) v1=(x1,y1) 和 v 2 = ( x 2 , y 2 ) \mathbf{v}_2=(x_2,y_2) v2=(x2,y2),则它们映射到高维特征空间后的内积可以写作:
可以看到在这个例子里,高维特征空间中两个点的内积,可以写成一个 关于原始空间中两个点的函数 κ ( ⋅ ; ⋅ ) \kappa(\cdot;\cdot) κ(⋅;⋅),这就是核函数。
特别地,上面的例子中,映射用的是多项式核,多项式的次数 d d d 取2。
为什么需要核函数
这里的例子为了计算方便,映射的空间维数依然很低,这里稍微解释一下 为什么需要核函数 ?假设原始空间是二维的,那么对于两个属性 x x x 和 y y y,取一阶二阶的组合只有5个(也即 x 2 x^2 x2, y 2 y^2 y2, x x x, y y y, x y xy xy)。
但当原始空间是三维的时候,仍然取一阶二阶,组合就多达19个了(也即 x x x, y y y, z z z, x y xy xy, x z xz xz, y z yz yz, x 2 y x^2y x2y, x 2 z x^2z x2z, y 2 x y^2x y2x, y 2 z y^2z y2z, z 2 x z^2x z2x, z 2 y z^2y z2y, x 2 y z x^2yz x2yz, x y 2 z xy^2z xy2z, x y z 2 xyz^2 xyz2, x 2 y 2 z x^2y^2z x2y2z, x 2 y z 2 x^2yz^2 x2yz2, x y 2 z 2 xy^2z^2 xy2z2, x y z xyz xyz)。
随着原始空间维数增长,新空间的维数是呈爆炸性上升的。何况现实中我们遇到的问题的原始空间往往本来就已经是高维的,如果再进行映射,新特征空间的维度是难以想象的。
然而有了核函数,我们就可以在原始空间中通过函数 κ ( ⋅ ; ⋅ ) \kappa(\cdot;\cdot) κ(⋅;⋅) 计算(这称为 核技巧(kernel trick)),而 不必直接计算高维甚至无穷维特征空间中的内积。
使用核函数后,对偶问题式(10)可以重写为:
max a ∑ i = 1 m a i − 1 2 ∑ i = 1 m ∑ j = 1 m a i a j y i y j κ ( x i ; x j ) s . t . ∑ i = 1 m a i y i = 0 , a i ≥ 0 , i = 1 , 2 , . . . , m ( 11 ) \max_{\mathbf{a}} \sum_{i=1}^m a_i - \frac{1}{2} \sum_{i=1}^m\sum_{j=1}^m a_i a_j y_i y_j \kappa(\mathbf{x}_i;\mathbf{x}_j) \quad s.t. \quad \sum_{i=1}^m a_i y_i = 0, \quad a_i \geq 0, \quad i=1,2,...,m \qquad (11) amaxi=1∑mai−21i=1∑mj=1∑maiajyiyjκ(xi;xj)s.t.i=1∑maiyi=0,ai≥0,i=1,2,...,m(11)
求解后得到的模型可以表示为:
这个式子表明了 模型最优解可通过训练样本的核函数展开,称为 支持向量展式(support vector expansion)。
显然,在需要对新样本进行预测时,我们 无需把新样本映射到高维(甚至无限维)空间,而是可以 利用保存下来的训练样本(支持向量)和核函数 κ \kappa κ 进行求解。
注意,核函数本身不等于映射!!! 它只是一个与 计算两个数据点映射到高维空间之后的内积 等价的函数。当我们发现数据在原始空间线性不可分时,会有把数据映射到高维空间来实现线性可分的想法,比方说引入原有属性的幂或者原有属性之间的乘积作为新的维度。
假设我们把数据点都映射到了一个维数很高甚至无穷维的特征空间,而 模型求解和预测的过程需要用到映射后两个数据点的内积,这时直接计算就没辙了。但我们又幸运地发现,原来 高维空间中两点的内积在数值上等于原始空间通过某个核函数算出的函数值,无需先映射再求值,就很好地解决了计算的问题了。
核函数的性质
核函数定理:给定一个输入空间 X \mathcal{X} X,函数 κ ( ⋅ ; ⋅ ) \kappa(\cdot;\cdot) κ(⋅;⋅) 是定义在 X × X \mathcal{X} \times \mathcal{X} X×X 上的 对称函数。当且仅当对于任意数据集 D = { x 1 , x 2 , . . . , x m } D = \{\mathbf{x}_1,\mathbf{x}_2,...,\mathbf{x}_m\} D={x1,x2,...,xm}, 对应的核矩阵(kernel matrix)K 都是半正定的时候, κ \kappa κ 是核函数。
核矩阵是一个规模为 m × m m \times m m×m 的函数矩阵,每个元素都是一个函数,比如第 i i i 行 j j j 列的元素是 κ ( x i , x j ) \kappa(\mathbf{x}_i,\mathbf{x}_j) κ(xi,xj)。只要一个对称函数所对应的核矩阵半正定,它就能作为核函数使用。事实上,对于一个半正定核矩阵,总能找到一个与之对应的映射。也即是说,任何一个核函数都隐式地定义了一个称为“再生核希尔伯特空间(Reproducing Kernel Hilbert Space,简称RKHS)”的特征空间。
做映射的初衷是希望 样本在新特征空间上线性可分,因此新特征空间的好坏直接决定了支持向量机的性能,但是我们并 不知道怎样的核函数是合适的,,而核函数也仅是隐式地定义了这个特征空间。于是,"核函数选择"成为支持向量机的最大变数。若核函数选择不合适,则意味着将样本映射到了一个不合适的特征空间,很可能导致性能不佳。
一般来说有以下几种常用核函数:
| 名称 | 表达式 | 参数 |
|---|---|---|
| 线性核 | κ ( x i , x j ) = x i T x j \kappa(\mathbf{x}_i,\mathbf{x}_j)=\mathbf{x}_i^T\mathbf{x}_j κ(xi,xj)=xiTxj | - |
| 多项式核 | κ ( x i , x j ) = ( x i T x j ) d \kappa(\mathbf{x}_i,\mathbf{x}_j)=(\mathbf{x}_i^T\mathbf{x}_j)^d κ(xi,xj)=(xiTxj)d | d ≥ 1 d \geq 1 d≥1为多项式的次数,d=1时退化为线性核 |
| 高斯核(亦称RBF核) | κ ( x i , x j ) = exp ( − ∥ x i − x j ∥ 2 2 σ 2 ) \kappa(\mathbf{x}_i,\mathbf{x}_j)=\exp (-\frac{\Vert \mathbf{x}_i-\mathbf{x}_j \Vert ^2}{2\sigma^2}) κ(xi,xj)=exp(−2σ2∥xi−xj∥2) | σ > 0 \sigma>0 σ>0 为高斯核的带宽(width) |
| 拉普拉斯核 | κ ( x i , x j ) = exp ( − ∥ x i − x j ∥ σ ) \kappa(\mathbf{x}_i,\mathbf{x}_j)=\exp (-\frac{\Vert \mathbf{x}_i-\mathbf{x}_j \Vert}{\sigma}) κ(xi,xj)=exp(−σ∥xi−xj∥) | σ > 0 \sigma>0 σ>0 |
| Sigmoid核 | κ ( x i , x j ) = tanh ( β x i T x j + θ ) \kappa(\mathbf{x}_i,\mathbf{x}_j)=\tanh(\beta \mathbf{x}_i^T\mathbf{x}_j+\theta) κ(xi,xj)=tanh(βxiTxj+θ) | t a n h tanh tanh 为双曲正切函数, β > 0 , θ < 0 \beta>0,\theta<0 β>0,θ<0 |
特别地,文本数据一般用线性核,情况不明可尝试高斯核。
除了这些常用的核函数,要 产生核函数还可以使用函数组合的方式:
-
若 κ 1 \kappa_1 κ1 和 κ 2 \kappa_2 κ2 都是核函数,则对于任意正数 a a a、 b b b,其线性组合 a κ 1 + b κ 2 a\kappa_1+b\kappa_2 aκ1+bκ2 也是核函数,其中 a > 0 , b > 0 a>0,b>0 a>0,b>0。
-
若 κ 1 \kappa_1 κ1 和 κ 2 \kappa_2 κ2 都是核函数,则其直积 κ 1 ⊗ κ 2 ( x , z ) = κ 1 ( x , z ) κ 2 ( x , z ) \kappa_1 \otimes \kappa_2(\mathbf{x},\mathbf{z}) = \kappa_1(\mathbf{x},\mathbf{z})\kappa_2(\mathbf{x},\mathbf{z}) κ1⊗κ2(x,z)=κ1(x,z)κ2(x,z) 也是核函数。
-
若 κ 1 \kappa_1 κ1 是核函数,则对于任意函数 g ( x ) g(\mathbf{x}) g(x), κ ( x , z ) = g ( x ) κ 1 ( x , z ) g ( z ) \kappa(\mathbf{x},\mathbf{z}) = g(\mathbf{x}) \kappa_1(\mathbf{x},\mathbf{z}) g(\mathbf{z}) κ(x,z)=g(x)κ1(x,z)g(z) 也是核函数。
软间隔与正则化
在前面的讨论中,我们一直假定训练样本在样本空间或特征空间中是线性可分的,即存在一个超平面能将不同类的样本完全划分开。然而,在现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分;退一步说,即使恰好找到了某个核函数使训练集在特征空间中线性可分,也很难断定这个貌似线性可分的结果不是由于 过拟合 所造成的。
比方说上面这张图,黑色虚线是此时的划分超平面,最大间隔很小。但事实上,黑色圆圈圈起的蓝点是一个 outlier,可能是噪声的原因,它偏离了正确的分布。而训练模型时,我们并没有考虑这一点,这就导致 把训练样本中的 outlier当成数据的真实分布拟合了,也即过拟合。但当我们 允许这个 outlier 被误分类 时,得到的划分超平面可能就如图中深红色线所示,此时的最大间隔更大,预测新样本时误分类的概率也会降低很多。
在实际任务中,outlier 的情况可能更加严重。比方说,如果图中的 outlier 再往右上移动一些距离的话,我们甚至会 无法构造出一个能将数据划分开的超平面。
缓解该问题的一个思路就是 允许支持向量机在一些样本上出错,为此,引入 软间隔(soft margin) 的概念。软间隔是相对于 硬间隔(hard margin) 的一个概念,硬间隔要求所有样本都必须划分正确,也即约束:
y i ( w T x i + b ) ≥ 1 y_i(\mathbf{w}^T\mathbf{x}_i+b) \geq 1 yi(wTxi+b)≥1
软间隔则 允许某些样本不满足约束(根据约束条件的不同,有可能某些样本出现在间隔内,甚至被误分类)。此时目标函数可以重写为:
min w , b 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ℓ 0 / 1 ( y i ( w T x + b ) − 1 ) ( 12 ) \min_{\mathbf{w},b} \frac{1}{2} \Vert \mathbf{w} \Vert^2 + C \sum_{i=1}^m \ell_{0/1}(y_i(\mathbf{w}^T\mathbf{x}+b)-1) \qquad (12) w,bmin21∥w∥2+Ci=1∑mℓ0/1(yi(wTx+b)−1)(12)
其中 ℓ 0 / 1 \ell_{0/1} ℓ0/1 是0/1损失函数:

它的含义很简单:如果分类正确,那么函数间隔必定大于等于1,此时损失为0;如果分类错误,那么函数间隔必定小于等于-1,此时损失为1。
而 C C C 则是一个大于0的常数,当 C C C 趋于无穷大时,式(12)等效于带约束的式(1),因为此时对误分类的惩罚无限大,也即要求全部样本分类正确。当 C C C 取有限值时,允许某些样本分类错误。
然而由于 0/1损失函数非凸、非连续,数学性质不太好,所以式(12)难以求解,于是在实际任务中,我们采用一些 凸的连续函数 来取替它,这样的函数就称为 替代损失(surrogate loss)函数。
最常用的有以下三种:
-
hinge损失: ℓ h i n g e ( z ) = max ( 0 , 1 − z ) \ell_{hinge}(z) = \max (0,1-z) ℓhinge(z)=max(0,1−z)
-
指数损失(exponential loss): ℓ exp ( z ) = exp ( − z ) \ell_{\exp}(z) = \exp (-z) ℓexp(z)=exp(−z)
-
对率损失(logistic loss): ℓ log ( z ) = log ( 1 + exp ( − z ) ) \ell_{\log}(z) = \log (1+\exp (-z) ) ℓlog(z)=log(1+exp(−z))
不妨作图观察比较一下这些损失函数(code文件夹下有 实现代码):
这里有个问题是,书中提到对率损失中 log \log log 指 ln \ln ln,也即底数为自然对数,但这种情况下对率损失在 z = 0 z=0 z=0 处不为1,而是0.693。但是书中的插图里,对率损失经过 ( 0 , 1 ) (0,1) (0,1) 点,此时底数应为2,上面的插图就是按底数为2计算的。
实际任务中 最常用的是hinge损失,这里就以hinge损失为例,替代0/1损失函数,此时目标函数式(12)可以重写为:
min w , b 1 2 ∥ w ∥ 2 + C ∑ i = 1 m max ( 0 , 1 − y i ( w T x + b ) ) ( 13 ) \min_{\mathbf{w},b} \frac{1}{2} \Vert \mathbf{w} \Vert^2 + C \sum_{i=1}^m \max(0, 1-y_i(\mathbf{w}^T\mathbf{x}+b)) \qquad (13) w,bmin21∥w∥2+Ci=1∑mmax(0,1−yi(wTx+b))(13)
引入 松弛变量(slack variables) ξ i ≥ 0 \xi_i \geq 0 ξi≥0,可以把式(13)重写为:
min w , b 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ξ i s . t . y i ( w T x + b ) ≥ 1 − ξ i , ξ i ≥ 0 , i = 1 , 2 , . . . , m ( 14 ) \min_{\mathbf{w},b} \frac{1}{2} \Vert \mathbf{w} \Vert^2 + C \sum_{i=1}^m \xi_i \quad s.t. \quad y_i(\mathbf{w}^T\mathbf{x}+b) \geq 1-\xi_i, \quad \xi_i \geq 0, \quad i=1,2,...,m \qquad (14) w,bmin21∥w∥2+Ci=1∑mξis.t.yi(wTx+b)≥1−ξi,ξi≥0,i=1,2,...,m(14)
该式描述的就是常用的 软间隔支持向量机,其中每个样本都对应着一个松弛变量,用以 表示该样本误分类的程度,松弛变量的值越大,程度越高。
求解软间隔支持向量机
式(14)仍然是一个二次规划问题,类似于前面的做法,分以下几步:
-
通过拉格朗日乘子法把 m m m 个约束转换 m m m 个拉格朗日乘子,得到该问题的拉格朗日函数。
-
分别对 w , b , ξ \mathbf{w}, b, \xi w,b,ξ 求偏导,代入拉格朗日函数得到对偶问题。
-
使用SMO算法求解对偶问题,解出所有样本对应的拉格朗日乘子。
-
需要进行新样本预测时,使用支持向量及其对应的拉格朗日乘子进行求解。
特别地,因为式(14)有 两组各 m m m 个不等式约束,所以该问题的拉格朗日函数有 a i ≥ 0 a_i \geq 0 ai≥0 和 μ i ≥ 0 \mu_i \geq 0 μi≥0 两组拉格朗日乘子。
特别地,对松弛变量 ξ \xi ξ 求导,令导数为0会得到一条约束式:
C = a i + μ i ( 15 ) C = a_i + \mu_i \qquad (15) C=ai+μi(15)
有意思的是,软间隔支持向量机的对偶问题和硬间隔几乎没有不同,只是约束条件修改了一下:
max a ∑ i = 1 m a i − 1 2 ∑ i = 1 m ∑ j = 1 m a i a j y i y j x i T x j s . t . ∑ i = 1 m a i y i = 0 , 0 ≤ a i ≤ C , i = 1 , 2 , . . . , m ( 16 ) \max_{\mathbf{a}} \sum_{i=1}^m a_i - \frac{1}{2} \sum_{i=1}^m\sum_{j=1}^m a_i a_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j \quad s.t. \quad \sum_{i=1}^m a_i y_i = 0, \quad 0 \leq a_i \leq C, \quad i=1,2,...,m \qquad (16) amaxi=1∑mai−21i=1∑mj=1∑maiajyiyjxiTxjs.t.i=1∑maiyi=0,0≤ai≤C,i=1,2,...,m(16)
这里的 a i a_i ai 不仅要求大于等于0,还要求小于等于 C C C。
类似地,由于式(14)的约束条件是 不等式约束,所以求解过程要求满足 KKT(Karush-Kuhn-Tucker)条件:
KKT条件可以理解为下面几点:
-
对任意训练样本,
- 要么对应的拉格朗日乘子 a i = 0 a_i=0 ai=0;
- 要么函数间隔等于1和对应的松弛变量之差( y i ( w T x + b ) = 1 − ξ i y_i(\mathbf{w}^T\mathbf{x}+b) = 1-\xi_i yi(wTx+b)=1−ξi)。
-
如果一个样本的拉格朗日乘子 a i = 0 a_i=0 ai=0,则它对模型没有任何影响,不需要保留。
-
如果一个样本的拉格朗日乘子大于0,则它是支持向量。
- 如果拉格朗日乘子 a i a_i ai 小于 C C C,按照式(15)有 μ i > 0 \mu_i>0 μi>0,
因此松弛变量 ξ i = 0 \xi_i=0 ξi=0,此时函数间隔为1,样本落在最大间隔边界上。 - 如果拉格朗日乘子 a i a_i ai 等于 C C C,按照式(15)有 μ i = 0 \mu_i=0 μi=0,因此松弛变量 ξ i > 0 \xi_i>0 ξi>0。
- 若 ξ i < 1 \xi_i<1 ξi<1,则样本落在间隔内,但依然被正确分类。
- 若 ξ i > 1 \xi_i>1 ξi>1,则样本落在另一个类的间隔外,被错误分类
- 如果拉格朗日乘子 a i a_i ai 小于 C C C,按照式(15)有 μ i > 0 \mu_i>0 μi>0,
上图就展示了一个典型的软间隔支持向量机。图中就有一些异常点,这些点有的虽然在虚线与超平面之间( 0 < y i ( w T x + b ) < 1 0 < y_i(\mathbf{w}^T\mathbf{x}+b) < 1 0<yi(wTx+b)<1),但也能被正确分类(比如 x 3 \mathbf{x}_3 x3)。有的点落到了超平面的另一侧,就会被误分类(比如 x 4 \mathbf{x}_4 x4 h和 x 5 \mathbf{x}_5 x5)。
特别地,在 R. Collobert. 的论文 Large Scale Machine Learning 中提到,常数 C C C 一般取训练集大小的倒数( C = 1 m C = \frac{1}{m} C=m1)。
支持向量机和逻辑回归的联系与区别
上面用的是hinge损失,不过我们也提到了还有其他一些替代损失函数,事实上,使用对率损失时,SVM得到的模型和LR是非常类似的。
支持向量机和逻辑回归的 相同点:
- 都是线性分类器,模型求解出一个划分超平面;
- 两种方法都可以增加不同的正则化项;
- 通常来说性能相当。
支持向量机和逻辑回归的 不同点:
-
LR使用对率损失,SVM一般用hinge损失;
-
在LR的模型求解过程中,每个训练样本都对划分超平面有影响,影响力随着与超平面的距离增大而减小,所以说 LR的解受训练数据本身的分布影响;SVM的模型只与占训练数据少部分的支持向量有关,所以说,SVM不直接依赖数据分布,所得的划分超平面不受某一类点的影响;
-
如果数据 类别不平衡 比较严重,LR需要先做相应处理再训练,SVM则不用;
-
SVM依赖于 数据表达的距离测度,需要先把数据 标准化,LR则不用(但实际任务中可能会为了方便选择优化过程的初始值而进行标准化)。如果数据的距离测度不明确(特别是高维数据),那么最大间隔可能就变得没有意义;
-
LR的输出有 概率意义,SVM的输出则没有;
-
LR可以直接用于 多分类任务,SVM则需要进行扩展(但更常用one-vs-rest);
-
LR使用的对率损失是光滑的单调递减函数,无法导出支持向量,解依赖于所有样本,因此预测开销较大;SVM使用的hinge损失有“零区域”,因此 解具有稀疏性(书中没有具体说明这句话的意思,但按我的理解是解出的拉格朗日乘子 a \mathbf{a} a 具有稀疏性,而不是权重向量 w \mathbf{w} w),从而不需用到所有训练样本。
在实际运用中,LR更常用于大规模数据集,速度较快;SVM适用于规模小,维度高的数据集。
在 Andrew NG 的课里讲到过:
-
如果Feature的数量很大,跟样本数量差不多,这时候选用 LR 或者是 Linear Kernel的SVM;
-
如果Feature的数量比较小,样本数量一般,不算大也不算小,选用 SVM + Gaussian Kernel;
-
如果Feature的数量比较小,而样本数量很多,需要手工添加一些 feature 变成第一种情况。
正则化
事实上,无论使用何种损失函数,SVM的目标函数都可以描述为以下形式:
min f Ω ( f ) + C ∑ i = 1 m ℓ ( f ( x i ) , y i ) ( 17 ) \min_f \Omega(f) + C \sum_{i=1}^m \ell(f(\mathbf{x}_i), y_i) \qquad (17) fminΩ(f)+Ci=1∑mℓ(f(xi),yi)(17)
在SVM中第一项用于描述划分超平面的“间隔”的大小,第二项用于描述在训练集上的误差。
更一般地,第一项称为 结构风险(structural risk),用来描述 模型的性质。第二项称为 经验风险(empirical risk),用来描述 模型与训练数据的契合程度。参数 C C C 用于对二者进行折中,权衡这两种风险。
前面学习的模型大多都是在最小化经验风险的基础上,再考虑结构风险(避免过拟合)。SVM却是从最小化结构风险来展开的。
-
从最小化经验风险的角度来看, Ω ( f ) \Omega(f) Ω(f) 表述了我们希望得到具有何种性质的模型(例如复杂度较小的模型),为引入领域知识和用户意图提供了路径(比方说贝叶斯估计中的先验概率)。
-
另一方面, Ω ( f ) \Omega(f) Ω(f) 还可以帮我们削减假设空间,从而降低模型过拟合的风险。从这个角度来看,可以称 Ω ( f ) \Omega(f) Ω(f) 为 正则化(regularization)项, C C C 为正则化常数。正则化可以看作一种 罚函数法,即对不希望出现的结果施以惩罚,从而使优化过程趋向于期望的目标。
L p L_p Lp 范数是常用的正则化项,其中 L 2 L_2 L2 范数 ∥ w ∥ 2 \Vert \mathbf{w} \Vert_2 ∥w∥2 倾向于 w \mathbf{w} w 的分量取值尽量 稠密,即非零分量个数尽量多; L 0 L_0 L0 范数 ∥ w ∥ 0 \Vert \mathbf{w} \Vert_0 ∥w∥0 和 L 1 L_1 L1 范数 ∥ w ∥ 1 \Vert \mathbf{w} \Vert_1 ∥w∥1 则倾向于 w \mathbf{w} w 的分量取值尽量 稀疏,即非零分量个数尽量少。
支持向量回归
同样是利用线性模型 f ( x ) = w T x + b f(\mathbf{x}) = \mathbf{w}^T\mathbf{x}+b f(x)=wTx+b 来预测,回归问题希望预测值和真实值 y y y 尽可能相近,而不是像分类任务那样,旨在令不同类的预测值可以被划分开。
传统的回归模型计算损失时直接取真实值 y y y 和预测值 f ( x ) f(x) f(x) 的差,当且仅当 y y y 与 f ( x ) f(x) f(x) 完全相同时,损失才为零,支持向量回归(Support Vector Regression,简称SVR) 则不然。SVR假设我们能容忍最多有 ϵ \epsilon ϵ 的偏差,只有当真实值和预测值之间相差超出了 ϵ \epsilon ϵ 时才计算损失。
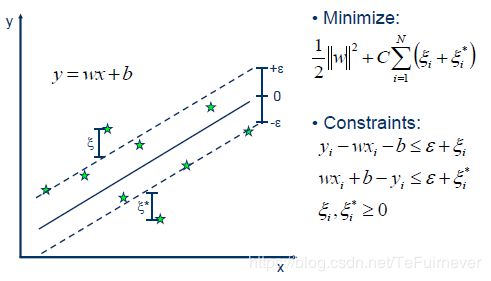
如图所示,以SVR拟合出的直线为中心,两边各构建出一个宽度为 ϵ \epsilon ϵ 的地带,落在这个 宽度为 2 ϵ 2\epsilon 2ϵ 的间隔带 内的点都被认为是预测正确的。
因此,问题可以形式化为目标函数:
min w , b 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ℓ ϵ ( f ( x i ) − y i ) ( 18 ) \min_{\mathbf{w},b} \frac{1}{2} \Vert \mathbf{w} \Vert^2 + C \sum_{i=1}^m \ell_{\epsilon}(f(\mathbf{x}_i) - y_i) \qquad (18) w,bmin21∥w∥2+Ci=1∑mℓϵ(f(xi)−yi)(18)
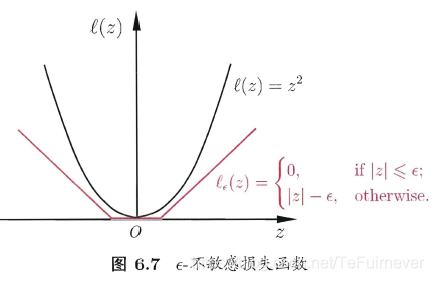
其中 C C C 为正则化常数, ℓ ϵ \ell_{\epsilon} ℓϵ 称为 ϵ − \epsilon- ϵ−不敏感损失( ϵ − \epsilon- ϵ−insensitive loss) 函数。定义如下:
引入松弛变量 ξ i \xi_i ξi 和 ξ ^ i \hat{\xi}_i ξ^i,分别表示 间隔带两侧的松弛程度,它们 可以设定为不同的值。此时,目标函数式(18)可以重写为:
min w , b 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ( ξ i + ξ ^ i ) ( 19 ) s . t . f ( x i ) − y i ≤ ϵ + ξ i , y i − f ( x i ) ≤ ϵ + ξ i ξ i ≥ 0 , ξ ^ i ≥ 0 , i = 1 , 2 , . . . , m . \min_{\mathbf{w},b} \frac{1}{2} \Vert \mathbf{w} \Vert^2 + C \sum_{i=1}^m (\xi_i + \hat{\xi}_i) \qquad (19)\\ s.t.\ f(\mathbf{x}_i) - y_i \leq \epsilon + \xi_i,\\ \qquad \quad y_i - f(\mathbf{x}_i) \leq \epsilon + \xi_i\\ \qquad \qquad \qquad \xi_i \geq 0, \hat{\xi}_i \geq 0, i=1,2,...,m. w,bmin21∥w∥2+Ci=1∑m(ξi+ξ^i)(19)s.t. f(xi)−yi≤ϵ+ξi,yi−f(xi)≤ϵ+ξiξi≥0,ξ^i≥0,i=1,2,...,m.
注意这里有四组 m m m 个约束条件,所以对应地有四组拉格朗日乘子。
![]()
接下来就是用拉格朗日乘子法获得问题对应的拉格朗日函数,然后求偏导再代回拉格朗日函数,得到对偶问题。然后使用SMO算法求解拉格朗日乘子,最后得到模型,这里不一一详述了。
特别地,SVR中同样有支持向量的概念,解具有稀疏性,所以训练好模型后不需保留所有训练样本。此外,SVR同样可以通过引入核函数来获得拟合非线性分布数据的能力。
核方法
无论是SVM还是SVR,如果不考虑偏置项 b,我们会发现模型总能表示为核函数的线性组合。更一般地,存在 表示定理(representer theorem):
令 H \mathbb{H} H 为核函数 κ \kappa κ 对应的再生希尔伯特空间, ∥ h ∥ H \Vert h \Vert_{\mathbb{H}} ∥h∥H 表示 H \mathbb{H} H 空间中关于 h h h 的范数,对于任意单调递增函数 Ω : [ 0 , ∞ ] ⟼ R \Omega:[0,\infty] \longmapsto \mathbb{R} Ω:[0,∞]⟼R 和任意非负损失函数 ℓ : R m ⟼ [ 0 , ∞ ] \ell:\mathbb{R}^m \longmapsto [0,\infty] ℓ:Rm⟼[0,∞],优化问题
m i n h ∈ H F ( h ) = Ω ( ∥ h ∥ H ) + ℓ ( h ( x 1 , h ( x 2 , . . . , h ( x m ) ) ( 20 ) min_{h \in \mathbb{H}} F(h) = \Omega(\Vert h \Vert_\mathbb{H}) + \ell(h(\mathbf{x}_1,h(\mathbf{x}_2,...,h(\mathbf{x}_m)) \qquad (20) minh∈HF(h)=Ω(∥h∥H)+ℓ(h(x1,h(x2,...,h(xm))(20)
的解总可写为:
h ∗ ( x ) = ∑ i = 1 m a i κ ( x , x i ) h^*(\mathbf{x}) = \sum_{i=1}^m a_i \kappa(\mathbf{x},\mathbf{x}_i) h∗(x)=i=1∑maiκ(x,xi)
这个定理表明,对于形如式(20),旨在最小化损失和正则化项之和的优化问题,表示定理对损失函数没有限制,对正则化项 Ω \Omega Ω 仅要求单调递增,甚至不要求 Ω \Omega Ω 是凸函数,意味着对于一般的损失函数和正则化项,最优解 h ∗ ( x ) h^*(\mathbf{x}) h∗(x) 都可以表示为核函数的线性组合。
基于核函数的学习方法,统称为 核方法(kernal methods)。最常见的就是通过 核化(引入核函数),将线性学习器扩展为非线性学习器,从而得到 “核线性判别分析” (Kernelized Linear DiscriminantAnalysis,简称KLDA)。这不仅限于SVM,事实上LR和LDA也都可以采用核函数,只是SVM使用hinge损失,解具有稀疏性,所以用得更多。
书中还介绍了如何核化LDA,这部分不作详细记录了。
分享一些蛮不错的问题和讲解,笔记中参考了部分内容:
- 支持向量机(SVM)是什么意思?
- 支持向量机中的函数距离和几何距离怎么理解?
- 几何间隔为什么是离超平面最近的点到超平面的距离?
- 支持向量机(support vector machine)–模型的由来
- SMO优化算法(Sequential minimal optimization)
- 机器学习有很多关于核函数的说法,核函数的定义和作用是什么?
- Linear SVM 和 LR 有什么异同?
- SVM与LR的比较
- SVM计算最优分类超平面时是否使用了全部的样本数据?
- 现在还有必要对SVM深入学习吗?
- SVM的核函数如何选取?
- 支持向量机通俗导论(理解SVM的三层境界)