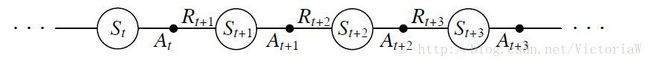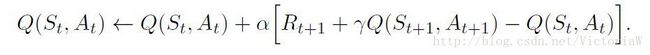西瓜书《机器学习》课后答案——chapter16_强化学习

1.用于K-摇臂赌博机的UCB（Upper Confidence Bound）方法每次选择 Q(k)+UC(k) 最大的摇臂，其中 Q(k) 为摇臂k当前的平均奖赏， UC(k) 为置信区间。例如：

Q(k)+2lnnnk−−−−−√

其中，n为已执行所有摇臂的总次数， nk 为已执行摇臂k的次数。比较UCB方法与 ϵ -贪心法和Softmax方法的异同。

解答：

ϵ -贪心：
- 在时刻 t ，为每个行为估计平均奖赏 Qt(a)
- 以 1−ϵ 的概率选择最大奖赏对应的行为

At=argmaxaQt(a)

- 以 ϵ 的概率等概率地从所有行为中选择一个

ϵ -贪心每次随机选择一个行为进行探索，没有对优质行为进行更多探索；另外如果一个行为已经执行很多次了，那么没有必要再对它进行探索了。

Softmax：
- 在时刻 t ，为每个行为估计平均奖赏 Qt(a)
- 以下面的概率分布选择行为

P(a)=eQt(a)τ∑Ki=1eQt(i)τ

Softmax方法平均奖励比较高的行为有更高的概率被选中。

UCB：
- 在时刻 t ，为每个行为估计平均奖赏 Qt(a) 以及 UCt(a)
- 选择 Qt(a)+UCt(a) 最大的那个行为

UCB中的 UCt(a) 是 Qt(a) 的置信区间。当一个行为执行次数比较少时，对应的 UC(a) 比较大，即置信区间比较大，意味着 Q(a) 不确定；当一个行为执行次数比较多时，对应的 UC(a) 比较小，即置信区间比较小，意味着 Q(a) 更准确。UCB每次探索的是不确定性高的行为。

参考：
https://www.cs.princeton.edu/courses/archive/fall16/cos402/lectures/402-lec22.pdf

2.借鉴图16.7，试写出基于 γ 折扣奖赏函数的策略评估算法。
解答：
书中对奖赏的定义和Sutton的书中（或者David Silver的课程）定义的不同。
西瓜书： Rax→x′ 表示从状态 x 采取行为 a 转移到状态 x′ 得到的奖励。

Sutton书： Ras=E[Rt+1|St=s,At=a] ：表示在状态 s 执行行为 a 的期望奖励。其中 Rt+1 表示立即奖励。

上述两个定义有两处不同：
- 第一个定义表示奖励和当前状态、行为、转移状态有关；而第二个定义表示奖励和转移后的状态无关，只和当前状态以及行为有关；
- 第一个定义在西瓜书中使用的时候是当做一个确定量使用的，即状态 x 时采取行为 a 转移到状态 x′ 对应的奖励是确定的；而第二个定义中是个期望，这意味着状态 s 采取行为 a 所得到的奖励是个随机变量。

这里和西瓜书保持一致。

输入：MDP四元组 E=<X,A,P,R>
被评估的策略 π
折扣因子 γ
小正数 θ
过程：
1: ∀x∈X ： V(x)=0
2: for k=1,2,⋯ :
3: Δ=0
4: for x in X:
5: V′(x)=∑a∈Aπ(x,a)∑x′∈XPax→x′(Rax→x′+γV(x′))
6: Δ=max(Δ,|V′(x)−V(x)|)
7: end for
8: if Δ<θ then
9: break
10: else
11: V=V’
12: end if
13: end for
输出：状态值函数 V

3. 借鉴图16.8，试写出基于 γ 折扣奖赏函数的策略迭代函数。
解答：

输入：MDP四元组 E=<X,A,P,R>
折扣因子 γ
小正数 θ
过程：
1: 初始化值函数以及策略： ∀x∈X ： V(x)=0 , π(x,a)=1|A(x)|
2: loop
3: for k=1,2,⋯ :
4: Δ=0
5: for x in X:
6: V′(x)=∑a∈Aπ(x,a)∑x′∈XPax→x′(Rax→x′+γV(x′))
7: Δ=max(Δ,|V′(x)−V(x)|)
8: end for
9: if Δ<θ then
10: break
11: else
12: V=V’
13: end if
14: end for
15: ∀x∈X ： π′(x)=argmaxaQ(x,a)
16: if ∀x∈X ： π′(x)=π(x) then
17: break
18: else
19: π=π′
20: end if
21: end loop
输出：最优策略 π

4.在没有MDP模型时，可以先学习MDP模型(例如使用随机策略进行采样，从样本中估计出转移函数和奖赏函数)，然后再使用有模型强化学习方法。试述该方法与免模型强化学习方法的优缺点。

解答：
基于模型的强化学习：
优点：
- 可以用有监督学习方法有效地学习模型
- 可以推理出模型的不确定性

缺点：
- 先学习模型，然后再构建值函数，导致会有两种估计误差

5.试推导出Sarsa算法的更新公式(16.31)。

解答：

（这个公式没有严格的推导过程，只是一个启发式更新）

采样是如下的序列：

公式(16.31)就是下面的式子（来自Sutton的《Reinforcement Learning: An Introduction》）：

表示如果从当前的状态-行为转移到下一个状态-行为，那么当前状态-行为的行为值函数可以认为是即时奖励与下一个状态-行为值函数之和（值函数的定义就是未来奖励的期望）。于是 Rt+1+γQ(St+1,At+1) 可以认为是 Q(St,At) 的目标。

可以看到这个更新公式中用到五元组 (St,At,Rt+1,St+1,At+1) ，这也是Sarsa名称的由来。

6.借鉴图16.14给出线性值函数近似Q-学习算法。

解答：

输入：
环境E；
动作空间A；
起始状态 x0 ；
奖赏折扣 γ ；
更新步长 α .
过程：
θ=0 ;
x=x0
for t=1,2,⋯ do
r,x′=在E中执行动作a=π(x)ϵ产生的奖赏与转移的状态
a′=π(x′)
θ=θ+α(r+γθT(x′;a′)−θT(x;a))(x;a) ；
π(x)=argmaxaθT(x;a) ；
x=x′
end for
输出：策略 π

7.线性值函数近似在实践中往往有较大误差。试结合BP神经网络，将线性值函数近似Sarsa算法推广为使用神经网络近似的Sarsa算法。
解答：
现在使用神经网络近似值函数 Q=f(x,a) 。网络输入为 (x,a) ，输出为相应的 Q 值。 Q 是未知的，那么在训练的时候输出label是什么呢？

在当前状态，根据 ϵ− 贪心策略执行行为 a ，可以获得立即奖赏 r 和转移状态 x′ 。在 x′ 处根据 ϵ− 贪心策略得到行为 a′ ，那么Sarsa给出的目标值为 r+γf(x′,a′) 。

8.试结合核方法，将线性值函数近似Sarsa算法推广为使用核函数的非线性值函数近似Sarsa算法。

9.对于目标驱动（goal-directed）的强化学习任务，目标是达到某一状态，例如将汽车驾驶到预定位置。试为这样的任务设置奖赏函数，并讨论不同奖赏函数的作用（例如每一步未达目标的奖赏为-、-1或1）。

10.与传统监督学习不同，直接模仿学习在不同时刻所面临的数据分布可能不同。试设计一个考虑不同时刻数据分布变化的模仿学习算法。