个人机器学习笔记之正则化

吴恩达机器学习笔记（3）——正则化

机器学习个人笔记，学习中水平有限，内容如有缺漏还请多多包涵
本章节笔记对应吴恩达课程的第8章。正则化给予所有参数一个缩小的趋势，防止高次项的参数过高出现过拟合现象。
因为θTX形式的线性模型只能做到欠拟合，这里我们不能使用θTX形来模拟过拟合现象，需要一个带有高次项变量的多项式模型来进行过拟合。

应用正则化的逻辑回归的python代码

import numpy as np
import matplotlib.pyplot as plt
import random

def sigmod(x):
    return 1/(1+np.exp(-x))

def h(x,pram):#假设函数 
    #datax是x1,x2,x1x2,x1^2,x2^2
    global tempx
    datax=np.hstack((x,tempx))#组合生成x1,x2,x1^2,x2^2矩阵
    temp=np.matmul(datax,pram[1:].reshape(datax.shape[1],1))+pram[0]#计算θTX

    return np.apply_along_axis(sigmod, 0, temp)

def logictic(a,itertimes,datax,datay,lam):#二变量梯度下降的逻辑回归
    #传进来是纯变量无高次项
    #a:学习率
    #itertimes:迭代次数
    #datax:数据集中的自变量部分
    #datay:数据集中的结果部分
    global tempx
    m=datax.shape[0]#训练集长度
    pram=np.zeros(datax.shape[1]+1+tempx.shape[1])#参数，初始化为0
    datax2=np.hstack((datax,tempx))
    temppram=np.zeros(pram.shape)#临时存储本次迭代的参数
    for i in range(0,itertimes):#迭代过程，执行itertimes次
        temppram[0]=pram[0]-a*(np.sum(h(datax,pram)-datay)+lam*pram[0]/m)#对参数theta0进行迭代 
        te=h(datax,pram)-datay
        for j in range(1,pram.shape[0]):#对剩余参数进行迭代 
            temppram[j]=pram[j]-a*(np.sum((h(datax,pram)-datay).T*datax2[...,j-1])+lam*pram[j]/m)          
        if i%10==0:
        print("迭代",i)
        print( "参数：",pram)  
        print("log误差:",np.sum(-datay*np.log(h(datax,pram))-(1-datay)*np.log(1-h(datax,pram))))#每十代输出误差
        pram=temppram
        pass
    return pram
    
def testerror(datax,datay,pram):#计算测试误差
    error=np.sum(-datay*np.log(h(datax,pram))-(1-datay)*np.log(1-h(datax,pram)))
    return error

x=np.zeros([100,2])#在10*10的样本空间中做逻辑回归
for i in range(0,10):    
    for j in range(0,10):       
        x[i*10+j][0]=i
        x[i*10+j][1]=j
x=x/10#将数据集范围缩小为从0到1避免计算高次项得到过大的结过
tempx=np.zeros([100,7])#生成高次项
tempx[...,0]=x[...,0]*x[...,0]#生成x1^2
tempx[...,1]=x[...,1]*x[...,1]#生成x2^2
tempx[...,2]=x[...,0]*x[...,1]#生成x1*x2
tempx[...,3]=x[...,0]*x[...,0]*x[...,1]#生成x1^2*x2
tempx[...,4]=x[...,1]*x[...,1]*x[...,0]#生成x2^2*x1
tempx[...,5]=x[...,0]*x[...,0]*x[...,0]#生成x1^3
tempx[...,6]=x[...,1]*x[...,1]*x[...,1]#生成x1^3
datax=np.hstack((x,tempx))#组合生成含高次项的变量矩阵
y=np.zeros([100,1])#训练集
testy=np.zeros([100,1])#测试集
for i in range(0,10):    
    for j in range(0,10):       
        if i+j-9>0:#数据集分类边界取直线y=-x+9
            y[i*10+j][0]=1
            testy[i*10+j][0]=1
        if random.random()>0.5 and i+j-9<2 and i+j-9>-2:
            y[i*10+j][0]=1#分界线边生成随机点
d=logictic(0.005, 1000, x, y,1)#执行逻辑回归算法，返回分类边界线的参数
print("测试集误差",testerror(x,testy,d))#输出测试误差

使用正则化的多项式逻辑回归：

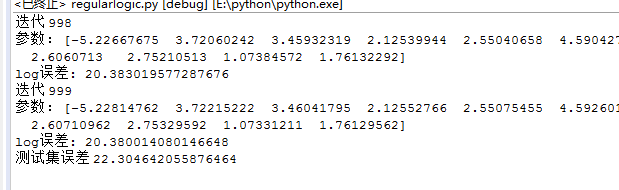
不使用正则化的多项式逻辑回归：

应用正则化的多项式线性回归的python代码（双变量）

这串代码相当用于y=ax1+bx2+cx1²+dx2²+c去拟合按照公式y=1+2x1+3x2生成的数据

import numpy as np

def h(x,pram):#假设函数，这里等价于y=ax1+bx2+cx1^2+dx2^2+c 
    pramt=np.array(pram[1:])
    temp2=np.zeros([x.shape[0],2])
    temp2[...,0]=x[...,0]*x[...,0]#生成x1^2
    temp2[...,1]=x[...,1]*x[...,1]#生成x2^2
    datax=np.hstack((x,temp2))#组合生成x1,x2,x1^2,x2^2矩阵
    return np.matmul(datax,pramt.reshape(len(pram)-1,1))+pram[0]

def gradientDescent(a,itertimes,datax,datay,lam):#双变量梯度下降的线性回归
    #a:学习率
    #itertimes:迭代次数
    #datax:数据集中的自变量部分
    #datay:数据集中的结果部分
    #正则化参数
    m=datax.shape[0]#训练集长度
    pram=np.zeros(datax.shape[1]+3)#参数，初始化为0
    temppram=np.zeros(pram.shape)#临时存储本次迭代的参数
    temp2=np.zeros([x.shape[0],2])
    temp2[...,0]=datax[...,0]*datax[...,0]#生成x1^2
    temp2[...,1]=datax[...,1]*datax[...,1]#生成x2^2
    datax2=np.hstack((datax,temp2))
    for i in range(0,itertimes):#迭代过程，执行itertimes次
        temppram[0]=pram[0]-a*(np.sum(h(datax,pram)-datay)+lam*pram[0])/m#对参数theta0进行迭代 
        for j in range(1,pram.shape[0]):#对剩余参数进行迭代 
            temppram[j]=pram[j]-a*(np.sum((h(datax,pram)-datay).reshape(1,m)*datax2[...,j-1])+lam*pram[j]/m)       
        if i%10==0:
            print("迭代",i)
            print( "参数：",pram)
            print("平方根误差:",np.sqrt(np.sum((h(datax,pram)-datay)**2)))#没十代
        pram=temppram
        pass
    return pram
def test(datax,pram,datay):#计算测试误差
    return np.sum(np.sqrt(np.sum((h(datax,pram)-datay)**2)))
    
x=np.random.rand(10,2)
pram=np.array([1,2,3])#真实参数
y=np.matmul(x,pram[1:].reshape(len(pram)-1,1))+pram[0]+np.random.rand(10,1)#生成训练数据集
p=gradientDescent(0.1, 1000, x, y,10)#执行梯度下降算法，返回预测参数，10为正则化参数，为0退化为普通梯度下降

datax=np.random.rand(10,2)
datay=np.matmul(datax,pram[1:].reshape(len(pram)-1,1))+pram[0]#生成测试集y=1+2*x1+3*x2
print("测试误差：",test(datax,p,datay))#计算测试误差

不使用正则化的多项式线性回归

使用正则化的多项式线性回归

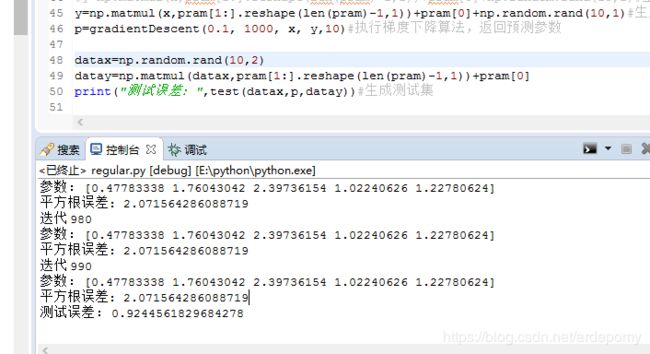
注：平方根误差代表训练误差

可见虽然使用正则化后训练误差加大了，但是测试误差变小了。
事实上不是每次结果都呈现出这样趋势，可能是生成数据集时引入的随机因素导致的

实现过程记录

使用正则化似乎会使收敛速度变慢。
几天后发现不是正则化导致逻辑回归的损失函数出现nan值，而是生成的数据集范围太大（0到10），计算高次项的时候变成了好几百，然后代入sigmoid函数（1/(1+exp^-x)）就因为浮点运算误差生成了1，随后在损失函数的log(1-h(x))里生成了nan值，解决方法是将生成的数据集x除以10。

公式部分

使用正则化的梯度下降的迭代公式:
$${\theta }_0={\theta }_0-a\ast \frac{1}{m}\sum _{i=0}^m(h_{\theta }(x^{(i)})-y^{(i)}).$$
$${\theta }_j={\theta }_j-a\ast \frac{1}{m}\sum _{i=0}^m(h_{\theta }(x^{(i)})-y^{(i)})\ast x_j^i+\frac{\lambda }{m}{\theta }_j.j<0<m$$
目前线性回归和逻辑回归都是使用梯度下降来最小化代价函数的，而正则化作用是在梯度下降算法上的，因此正则化对于线性回归和逻辑回归的公式是相同的。

其他笔记

• 机器学习入门
  - 目录