个人机器学习笔记之Kmeans

吴恩达机器学习笔记（5）——K-Means

机器学习个人笔记，学习中水平有限，内容如有缺漏欢迎指正。

序言

神经网络又鸽了。其实神经网络的视频已经看过一遍了，但是一直嫌麻烦，觉得写起来要花太长时间（主要是因为不想调库，觉得用调库做对原理理解没有帮助），就先看了其他章的视频。这次就看了无监督学习（第13章）的K-Means算法，并用python实现了。

K-Means算法原理口述

无监督学习中，数据是没有标注的，也就是说数据集中没有一个y告诉你什么是正确的分类。
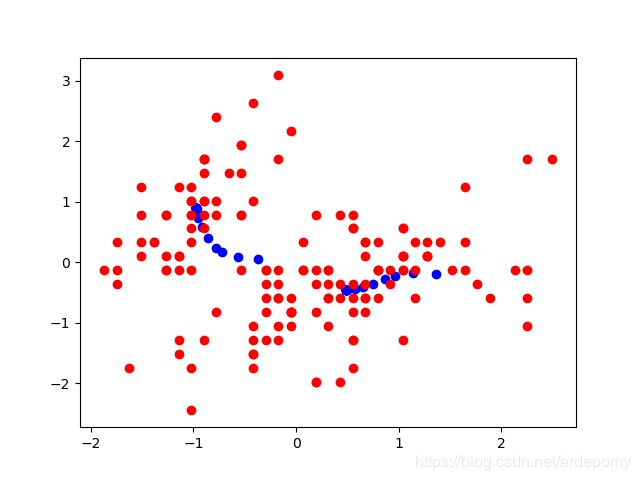
无监督学习中的数据集就像这样，给出一组数据点，我们的算法需要自行将数据分为几类。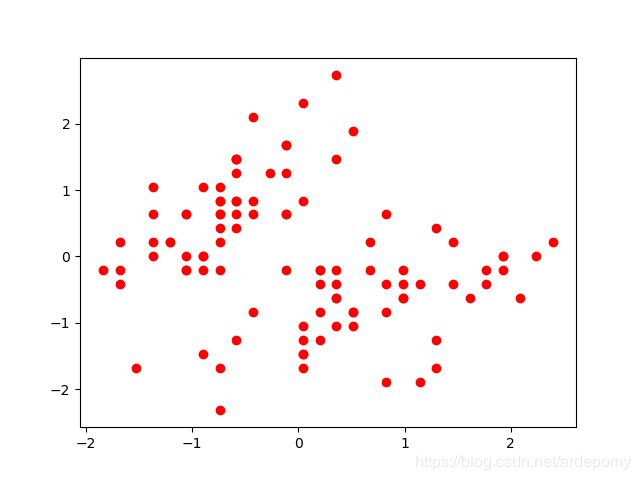
算法首先选取几个随机点（有几个分类就选几个）作为初始聚类中心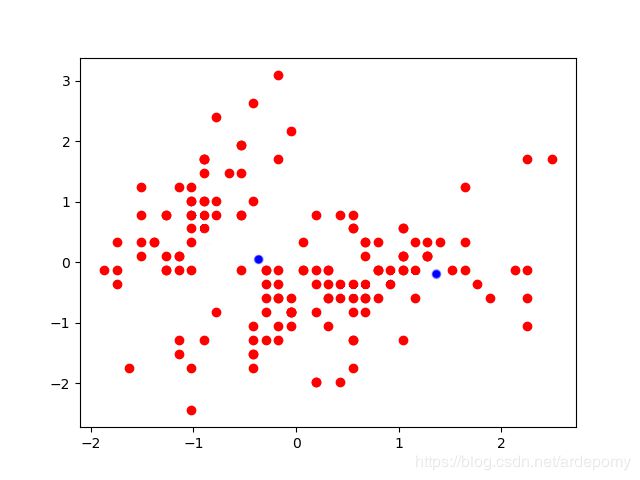
然后对于每个样本点，按照距离哪个聚类中心更近就属于哪个聚类中心的原则划分类别

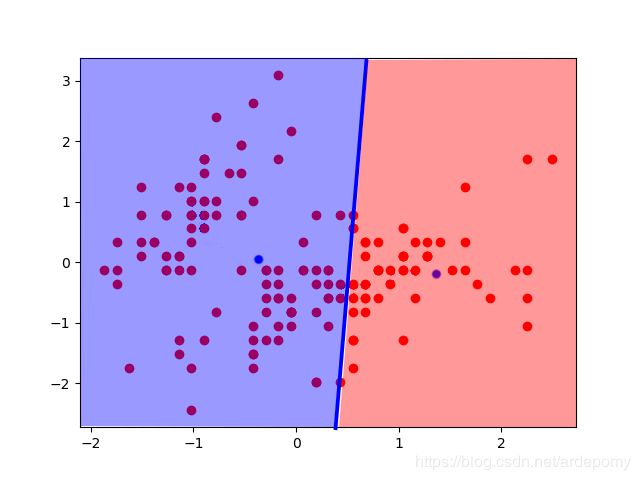
找到每个分类好的样本点群的中心点，将聚类中心移到这个中心点

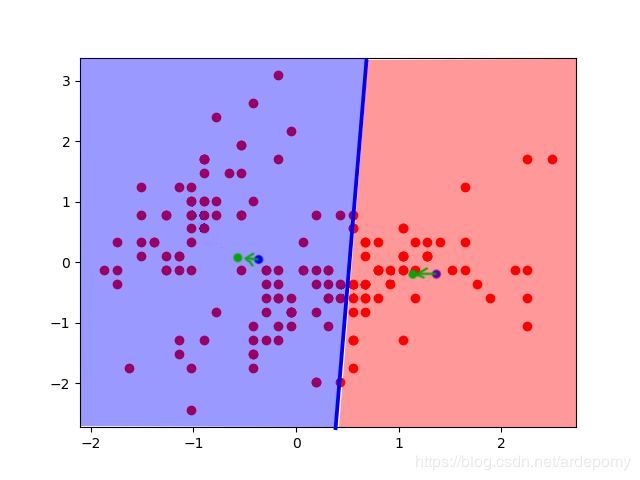
不断迭代，直到聚类中心的变化不再明显

K-Means的python代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler

def getcenter(x):#获取一群给定样本的中心
   x1=x[:,0]
   x2=x[:,1]
   return np.array([(np.sum(x1)/x.shape[0]),(np.sum(x2)/x.shape[0])])
   
def distance(x,y):    
   return np.sqrt(np.sum((x-y)**2))
   
def getdistances(x,c):#获取每个点离得最近的聚类中心的序号 
   alldistan=np.zeros([x.shape[0],1])   
   for i in range(0,x.shape[0]):#对于每个样本点 
       distan=np.zeros([x.shape[0],c.shape[0]])
       for j in range(0,c.shape[0]):
           distan[i,j]=distance(x[i,:], c[j,:])       
       alldistan[i]=np.argsort(distan[i,:])[0]#离哪个聚类中心距离最小
   return alldistan

def calculaterror(x):#计算“损失值”
   global c
   dis=getdistances(x, c).astype(np.int32)  
   return distance(x,c[dis[:,0],:])/c.shape[0]

def kmean(step,x):#c为初始聚类中心
   global c 
   for i in range(step):
       distan=getdistances(x, c)
       for j in range(c.shape[0]):#根据distance划分聚类
           c[j]=getcenter(x[distan[:,0]==j,:])#移动聚类中心到新的位置
       
iris = datasets.load_iris()#引入iris数据集
X = iris.data

X = X[:,:2]# 只取前两个特征
standardScaler = StandardScaler()
standardScaler.fit(X)
X_standard = standardScaler.transform(X)#对数据进行归一化

x=np.array(X_standard)
c=np.random.rand(2,2)*4-2#初始随机化的聚类中心

kmean(20, x)#进行20代kmeans算法
print("损失值:",calculaterror(x))#计算“损失值“并输出

center=getcenter(c)##聚类分界线必经过的点
k=-(c[0,0]-c[1,0])/(c[0,1]-c[1,1])#聚类分界线斜率=-(x1-x2)/(y1-y2)

plt.scatter(X_standard[:,0], X_standard[:,1], color='red')
plt.scatter(c[:,0], c[:,1], color='blue')
plt.plot(np.linspace(-2, 2, 2),k*np.linspace(-2, 2, 2)-k*center[0]+center[1])#绘制聚类分界线
plt.show()

运行结果，注意此图横纵比例不是1：1，所以分类直线看起来不垂直于两个聚类中心构成的直线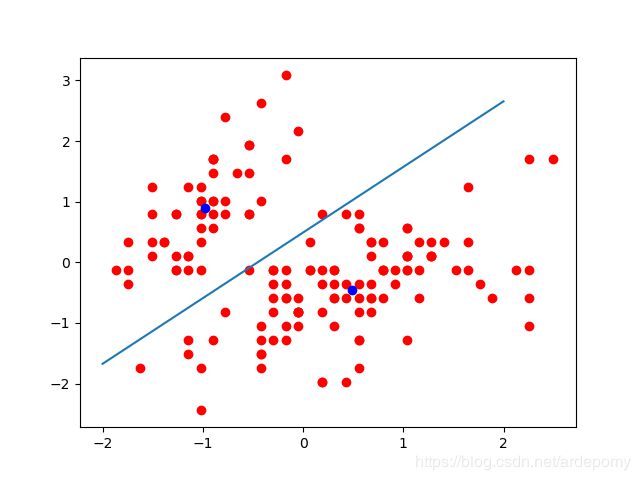

实现过程记录

公式部分

K-Means的损失函数公式：

$$\frac{1}{m}\sum _{i=1}^m||x^{(i)}-{\mu }_{c(i)}|{|}^2$$
该式意为对于当前每个聚类中心，计算属于该聚类中心的所有样本到其的欧几里得距离之和，然后除以分类个数

学习视频

无监督学习

其他笔记

• 机器学习入门
  - 目录