插入排序(Insertion Sort)以及优化改进
介绍:
插入排序是一种简单直观的排序算法。它的工作原理非常类似于我们抓扑克牌
对于未排序数据(右手抓到的牌),在已排序序列(左手已经排好序的手牌)中从后向前扫描,找到相应位置并插入。
插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
具体算法描述如下:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
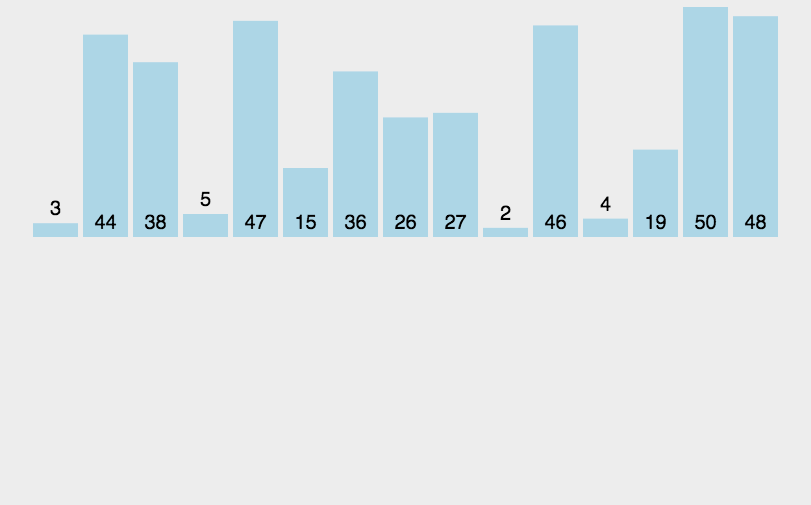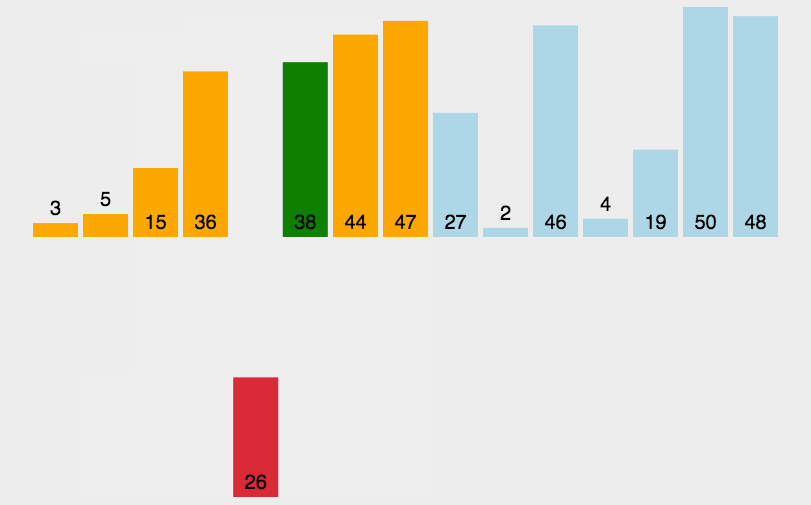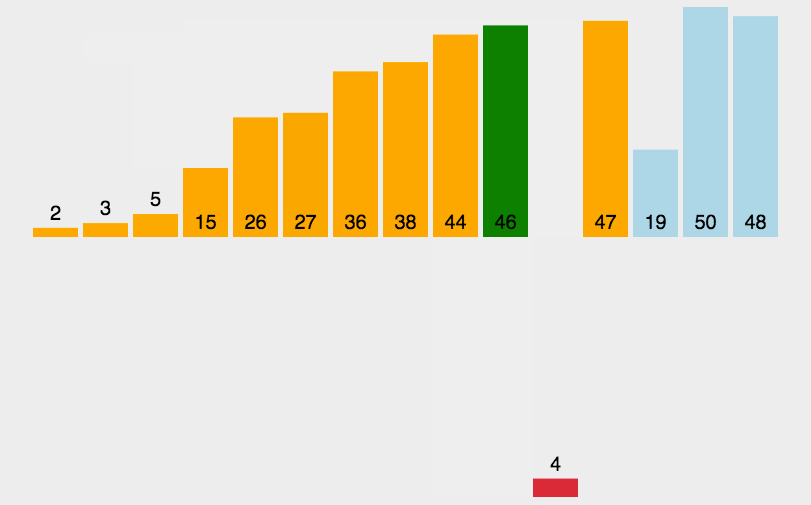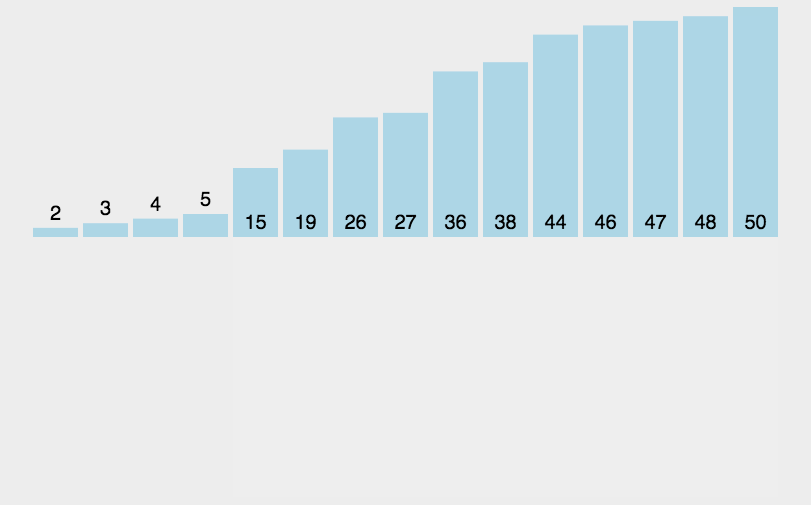
对序列{ 6, 5, 3, 1, 8, 7, 2, 4 }进行插入排序的实现过程如下
Java代码示例:
package com.insertsort;
//分类 ------------- 内部比较排序
//数据结构 ---------- 数组
//最差时间复杂度 ---- 最坏情况为输入序列是降序排列的,此时时间复杂度O(n^2)
//最优时间复杂度 ---- 最好情况为输入序列是升序排列的,此时时间复杂度O(n)
//平均时间复杂度 ---- O(n^2)
//所需辅助空间 ------ O(1)
//稳定性 ------------ 稳定
public class Insert {
public void insertionSort(int array[]) { // 定义一个排序数组
// 假设当前数组第一个,即下标为0的数是已经排好的序,因此,起始位置是第二个数(下标为1)
for (int i = 1; i < array.length; i++) {
int preIndex = i - 1; // 当前已经排好序的
int current = array[i]; // 当前需要排序的数(从数组第二个开始,1号下标)
// 将当前需要排序的数与已排好的数从右到左依次比较,满足以下条件:已存在有排好的数;当前数与已排好的数相比较,当前数小于已排好的数,就往前依次比较,直到找到当前数大于等于已排数,即是当前数该排的位置。
while (preIndex >= 0 && array[preIndex] > current) { //开始时:1号下标数与0号下标数相比较
array[preIndex + 1] = array[preIndex]; // 如果已排好序的数比当前数大,就将其往右移动
preIndex--;
}
// 直到已排的数比当前数小(或者相等),将当前数插入到已排好序的数的右边(相等元素的相对次序未变,所以插入排序是稳定的)
array[preIndex + 1] = current;
}
}
}
测试代码:
package com.insertsort;
public class Test {
public static void main(String[] args) {
Insert insert = new Insert();
int array[] = { 6, 5, 3, 1, 8, 7, 2, 4 };
insert.insertionSort(array);
System.out.println("插入排序结果:");
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
}
}
动态演示图实例:
插入排序不适合对于数据量比较大的排序应用。但是,如果需要排序的数据量很小,比如量级小于千,那么插入排序还是一个不错的选择。 插入排序在工业级库中也有着广泛的应用,在STL的sort算法和stdlib的qsort算法中,都将插入排序作为快速排序的补充,用于少量元素的排序(通常为8个或以下)。
插入排序的改进:二分插入排序
对于插入排序,如果比较操作的代价比交换操作大的话,可以采用二分查找法来减少比较操作的次数,我们称为二分插入排序
Java实现代码
package com.insertsort;
/**
* 二分插入排序法
* 分类 -------------- 内部比较排序
* 数据结构 ---------- 数组 最差时间复杂度 ---- O(n^2)
* 最优时间复杂度 ---- O(nlogn)
* 平均时间复杂度 ---- O(n^2)
* 所需辅助空间 ------ O(1)
* 稳定性 ------------稳定
*
* @author Lenovo
*
*/
public class IsertSortDichotomy {
public void insertionSortDichotomy(int array[]) {
for (int i = 1; i < array.length; i++) {
int get = array[i]; // 右手抓到一张扑克牌
int left = 0; // 拿在左手上的牌总是排序好的,所以可以用二分法
int right = i - 1; // 手牌左右边界进行初始化
while (left <= right) { // 采用二分法定位新牌的位置
int min = (left + right) / 2;
if (array[min] > get) {
right = min - 1;
} else {
left = min + 1;
}
}
for (int j = i - 1; j >= left; j--) { // 将欲插入新牌位置右边的牌整体向右移动一个单位
array[j + 1] = array[j];
}
array[left] = get; // 将抓到的牌插入手牌
}
}
}
测试:
IsertSortDichotomy iDichotomy = new IsertSortDichotomy();
int array1[] = { 5, 2, 9, 4, 7, 6, 1, 3, 8 };
iDichotomy.insertionSortDichotomy(array1);
System.out.println("二分插入排序结果:");
for (int i = 0; i < array1.length; i++) {
System.out.print(array1[i] + " ");
}
插入排序的更高效改进:希尔排序(Shell Sort)
介绍:
1959年Shell发明,第一个突破O(n2)的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
希尔排序,也叫递减增量排序,是插入排序的一种更高效的改进版本。希尔排序是不稳定的排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序,算法的最后一步就是普通的插入排序,但是到了这步,需排序的数据几乎是已排好的了(此时插入排序较快)。
假设有一个很小的数据在一个已按升序排好序的数组的末端。如果用复杂度为O(n^2)的排序(冒泡排序或直接插入排序),可能会进行n次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据,所以小数据只需进行少数比较和交换即可到正确位置。
动态演示图:
Java代码示例:
package com.insertsort;
//分类 -------------- 内部比较排序
//数据结构 ---------- 数组
//最差时间复杂度 ---- 根据步长序列的不同而不同。已知最好的为O(n(logn)^2)
//最优时间复杂度 ---- O(n)
//平均时间复杂度 ---- 根据步长序列的不同而不同。
//所需辅助空间 ------ O(1)
//稳定性 ------------ 不稳定
public class Shell {
public void shellSort(int array[]) {
int h = 0;
while (h <= array.length) { // 生成初始增量
h = 3 * h + 1;
}
while (h >= 1) {
for (int i = h; i < array.length; i++) {
int j = i - h;
int get = array[i];
while (j >= 0 && array[j] > get) {
array[j + h] = array[j];
j = j - h;
}
array[j + h] = get;
}
h = (h - 1) / 3; // 递减增量
}
}
}
测试:
Shell shell = new Shell();
int array2[] = { 5, 2, 9, 4, 7, 6, 1, 3, 8 };
shell.shellSort(array2);
System.out.println("希尔排序结果:");
for (int i = 0; i < array2.length; i++) {
System.out.print(array2[i] + " ");
}
希尔排序是不稳定的排序算法,虽然一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱。
比如序列:{ 3, 5, 10, 8, 7, 2, 8, 1, 20, 6 },h=2时分成两个子序列 { 3, 10, 7, 8, 20 } 和 { 5, 8, 2, 1, 6 } ,未排序之前第二个子序列中的8在前面,现在对两个子序列进行插入排序,得到 { 3, 7, 8, 10, 20 } 和 { 1, 2, 5, 6, 8 } ,即 { 3, 1, 7, 2, 8, 5, 10, 6, 20, 8 } ,两个8的相对次序发生了改变。
参考:https://www.cnblogs.com/onepixel/articles/7674659.html http://www.cnblogs.com/eniac12/p/5329396.html