一、神经网络
1、神经元概述
神经网络是由一个个的被称为“神经元”的基本单元构成,单个神经元的结构如下图所示:
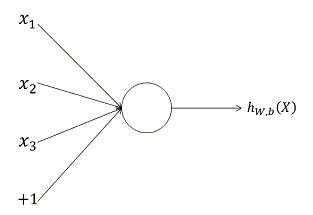
对于上述的神经元,其输入为 x1 x 1 , x2 x 2 , x3 x 3 以及截距 +1 + 1 ,其输出为:
hW,b(x)=f(WTx)=f(∑i=13Wixi+b) h W , b ( x ) = f ( W T x ) = f ( ∑ i = 1 3 W i x i + b )
其中, W W 表示的是向量,代表的是权重,函数 f f 称为激活函数,通常激活函数可以选择为Sigmoid函数,或者tanh双曲正切函数,其中,Sigmoid函数的形式为:
f(z)=11+e−z f ( z ) = 1 1 + e − z
双曲正切函数的形式为:
f(z)=tanh(z)=ez−e−zez+e−z f ( z ) = t a n h ( z ) = e z − e − z e z + e − z
以下分别是Sigmoid函数和tanh函数的图像,左边为Sigmoid函数的图像,右边为tanh函数的图像:
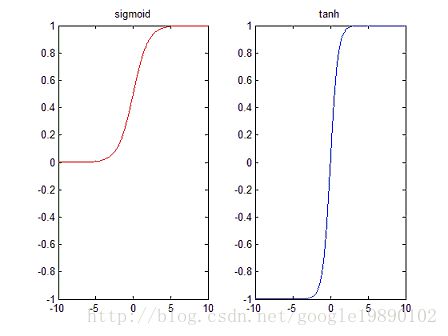
Sigmoid函数的区间为 [0,1] [ 0 , 1 ] ,而tanh函数的区间为 [−1,1] [ − 1 , 1 ] 。
若是使用sigmoid作为神经元的激活函数,则当神经元的输出为 1 1 时表示该神经元被激活,否则称为未被激活。同样,对于激活函数是tanh时,神经元的输出为 1 1 时表示该神经元被激活,否则称为未被激活。
2、神经网络
2.1、神经网络的结构
神经网络是由很多的神经元联结而成的,一个简单的神经网络的结构如下图所示:
其中一个神经元的输出是另一个神经元的输入, +1 + 1 项表示的是偏置项。上图是含有一个隐含层的神经网络模型, L1 L 1 层称为输入层, L2 L 2 层称为隐含层, L3 L 3 层称为输出层。
2.2、神经网络中的参数说明
在神经网络中,主要有如下的一些参数标识:
- 网络的层数 n1 n 1 。在上述的神经网络中 nl=3 n l = 3 ,将第 l l 层记为 Ll L l ,则上述的神经网络,输入层为 L1 L 1 ,输出层为 L3 L 3 。
- 网络权重和偏置 (W,b)=(W(1),b(1),W(2),b(2)) ( W , b ) = ( W ( 1 ) , b ( 1 ) , W ( 2 ) , b ( 2 ) ) ,其中 W(l)ij W i j ( l ) 表示的是第 l l 层的第 j j 个神经元和第 l+1 l + 1 层的第 i i 个神经元之间的连接参数, b(l)i b i ( l ) 标识的是第 l+1 l + 1 层的第 i i 个神经元的偏置项。在上图中, W(1)∈ℜ3×3 W ( 1 ) ∈ ℜ 3 × 3 , W(2)∈ℜ1×3 W ( 2 ) ∈ ℜ 1 × 3 。
2.3、神经网络的计算
在神经网络中,一个神经元的输出是另一个神经元的输入。假设 z(l)i z i ( l ) 表示的是第 l l 层的第 i i 个神经元的输入,假设 a(l)i a i ( l ) 表示的是第 l l 层的第 i i 个神经元的输出,其中,当 l=1 l = 1 时, a(1)i=xi a i ( 1 ) = x i 。根据上述的神经网络中的权重和偏置,就可以计算神经网络中每一个神经元的输出,从而计算出神经网络的最终的输出 hW,b h W , b 。
对于上述的神经网络结构,有下述的计算:
z(2)1=W(1)11x1+W(1)12x2+W(1)13x3+b(1)1 z 1 ( 2 ) = W 11 ( 1 ) x 1 + W 12 ( 1 ) x 2 + W 13 ( 1 ) x 3 + b 1 ( 1 )
a(2)1=f(W(1)11x1+W(1)12x2+W(1)13x3+b(1)1) a 1 ( 2 ) = f ( W 11 ( 1 ) x 1 + W 12 ( 1 ) x 2 + W 13 ( 1 ) x 3 + b 1 ( 1 ) )
z(2)2=W(1)21x1+W(1)22x2+W(1)23x3+b(1)2 z 2 ( 2 ) = W 21 ( 1 ) x 1 + W 22 ( 1 ) x 2 + W 23 ( 1 ) x 3 + b 2 ( 1 )
a(2)2=f(W(1)21x1+W(1)22x2+W(1)23x3+b(1)2) a 2 ( 2 ) = f ( W 21 ( 1 ) x 1 + W 22 ( 1 ) x 2 + W 23 ( 1 ) x 3 + b 2 ( 1 ) )
z(2)3=W(1)31x1+W(1)32x2+W(1)33x3+b(1)3 z 3 ( 2 ) = W 31 ( 1 ) x 1 + W 32 ( 1 ) x 2 + W 33 ( 1 ) x 3 + b 3 ( 1 )
a(2)3=f(W(1)31x1+W(1)32x2+W(1)33x3+b(1)3) a 3 ( 2 ) = f ( W 31 ( 1 ) x 1 + W 32 ( 1 ) x 2 + W 33 ( 1 ) x 3 + b 3 ( 1 ) )
从而,上述神经网络结构的最终的输出结果为:
hW,b(x)=f(W(2)11a(2)1+W(2)12a(2)2+W(2)13a(2)3+b(2)1) h W , b ( x ) = f ( W 11 ( 2 ) a 1 ( 2 ) + W 12 ( 2 ) a 2 ( 2 ) + W 13 ( 2 ) a 3 ( 2 ) + b 1 ( 2 ) )
上述的步骤称为前向传播,指的是信号从输入层,经过每一个神经元,直到输出神经元的传播过程。
2.4、其他形式的神经网络模型
上述以单隐层神经网络为例介绍了神经网络的基本结构,在神经网络的结构中,可以包含多个隐含层,神经网络的输出神经单元也可以是多个,如下面的含多隐层多输出单元的神经网络模型:
2.5、神经网络中参数的求解
对于上述神经网络模型,假设有 m m 个训练样本 {(x(1),y(1)),⋯,(x(m),y(m))} { ( x ( 1 ) , y ( 1 ) ) , ⋯ , ( x ( m ) , y ( m ) ) } ,对于一个训练样本 (x,y) ( x , y ) ,其损失函数为:
J(W,b;x,y)=12‖‖hW,b(x)−y‖‖2 J ( W , b ; x , y ) = 1 2 ‖ h W , b ( x ) − y ‖ 2
为了防止模型的过拟合,在损失函数中会加入正则项,即:
J=loss+R J = l o s s + R
其中, loss l o s s 表示的是损失函数, R R 表示的是正则项。则对于上述的含有 m m 个样本的训练集,其损失函数为:
J(W,b)=[1m∑i=1mJ(W,b;x(i),y(i))]+λ2∑l=1nl−1∑i=1sl∑j=1sl+1(W(l)ij)2 J ( W , b ) = [ 1 m ∑ i = 1 m J ( W , b ; x ( i ) , y ( i ) ) ] + λ 2 ∑ l = 1 n l − 1 ∑ i = 1 s l ∑ j = 1 s l + 1 ( W i j ( l ) ) 2
通常,偏置项并不放在正则化中,因为在正则化中放入偏置项只会对神经网络产生很小的影响。
我们的目标是要求得参数 W W 和参数 b b 以使得损失函数 J(W,b) J ( W , b ) 达到最小值。首先需要对参数进行随机初始化,即将参数初始化为一个很小的接近 0 0 的随机值。
参数的初始化有很多不同的策略,基本的是要在 0 0 附近的很小的邻域内取得随机值。
在随机初始化参数后,利用前向传播得到预测值 hW,b(x) h W , b ( x ) ,进而可以得到损失函数,此时需要利用损失函数对其参数进行调整,可以使用梯度下降的方法,梯度下降对参数的调整如下:
W(l)ij=W(l)ij−α∂∂W(l)ijJ(W,b) W i j ( l ) = W i j ( l ) − α ∂ ∂ W i j ( l ) J ( W , b )
b(l)i=b(l)i−α∂∂b(l)iJ(W,b) b i ( l ) = b i ( l ) − α ∂ ∂ b i ( l ) J ( W , b )
其中, α α 称为学习率,在计算参数的更新公式中,需要使用到反向传播算法。
而 ∂∂W(l)ijJ(W,b) ∂ ∂ W i j ( l ) J ( W , b ) , ∂∂b(l)iJ(W,b) ∂ ∂ b i ( l ) J ( W , b ) 的具体形式如下:
∂∂W(l)ijJ(W,b)=[1m∑i=1m∂∂W(l)ijJ(W,b;x(i),y(i))]+λW(l)ij ∂ ∂ W i j ( l ) J ( W , b ) = [ 1 m ∑ i = 1 m ∂ ∂ W i j ( l ) J ( W , b ; x ( i ) , y ( i ) ) ] + λ W i j ( l )
∂∂b(l)iJ(W,b)=1m∑i=1m∂∂b(l)iJ(W,b;x(i),y(i)) ∂ ∂ b i ( l ) J ( W , b ) = 1 m ∑ i = 1 m ∂ ∂ b i ( l ) J ( W , b ; x ( i ) , y ( i ) )
反向传播算法的思路如下:对于给定的训练数据 (x,y) ( x , y ) ,通过前向传播算法计算出每一个神经元的输出值,当所有神经元的输出都计算完成后,对每一个神经元计算其“残差”,如第 l l 层的神经元 i i 的残差可以表示为 δ(l)i δ i ( l ) 。该残差表示的是该神经元对最终的残差产生的影响。这里主要分为两种情况,一是神经元为输出神经元,第二是神经元为非输出神经元。这里假设 z(l)i z i ( l ) 表示第 l l 层上的第 i i 个神经元的输入加权和,假设 a(l)i a i ( l ) 表示的是第 l l 层上的第 i i 个神经元的输出, 即 a(l)i=f(z(l)i) a i ( l ) = f ( z i ( l ) ) 。
- 对于输出层 nl n l 上的神经元 i i ,其残差为:
δ(nl)i=∂∂znliJ(W,b;x,y)=∂∂znli12‖‖y−hW,b(x)‖‖2=∂∂znli12∑snli=1‖‖yi−anli‖‖2=(yi−anli)⋅(−1)⋅∂∂znlianli=−(yi−anli)⋅f′(znli) δ i ( n l ) = ∂ ∂ z i n l J ( W , b ; x , y ) = ∂ ∂ z i n l 1 2 ‖ y − h W , b ( x ) ‖ 2 = ∂ ∂ z i n l 1 2 ∑ i = 1 s n l ‖ y i − a i n l ‖ 2 = ( y i − a i n l ) ⋅ ( − 1 ) ⋅ ∂ ∂ z i n l a i n l = − ( y i − a i n l ) ⋅ f ′ ( z i n l )
-对于非输出层,即对于 l=nl−1,nl−2,⋯,2 l = n l − 1 , n l − 2 , ⋯ , 2 各层,第 l l 层的残差的计算方法如下(以第 nl−1 n l − 1 层为例):
δ(nl−1)i=∂∂znl−1iJ(W,b;x,y)=∂∂znl−1i12‖‖y−hW,b(x)‖‖2=∂∂znl−1i12∑snlj=1‖‖yj−anlj‖‖2=12∑snlj=1∂∂znl−1i‖‖yj−anlj‖‖2=12∑snlj=1∂∂znlj‖‖yj−anlj‖‖2⋅∂∂znl−1iznlj=∑snlj=1δ(nl)j⋅∂∂znl−1iznlj=∑snlj=1(δ(nl)j⋅∂∂znl−1i∑snl−1k=1f(znl−1k)⋅Wnl−1jk)=∑snlj=1(δ(nl)j⋅Wnl−1ji⋅f′(znl−1i))=(∑snlj=1δ(nl)j⋅Wnl−1ji)⋅f′(znl−1i) δ i ( n l − 1 ) = ∂ ∂ z i n l − 1 J ( W , b ; x , y ) = ∂ ∂ z i n l − 1 1 2 ‖ y − h W , b ( x ) ‖ 2 = ∂ ∂ z i n l − 1 1 2 ∑ j = 1 s n l ‖ y j − a j n l ‖ 2 = 1 2 ∑ j = 1 s n l ∂ ∂ z i n l − 1 ‖ y j − a j n l ‖ 2 = 1 2 ∑ j = 1 s n l ∂ ∂ z j n l ‖ y j − a j n l ‖ 2 ⋅ ∂ ∂ z i n l − 1 z j n l = ∑ j = 1 s n l δ j ( n l ) ⋅ ∂ ∂ z i n l − 1 z j n l = ∑ j = 1 s n l ( δ j ( n l ) ⋅ ∂ ∂ z i n l − 1 ∑ k = 1 s n l − 1 f ( z k n l − 1 ) ⋅ W j k n l − 1 ) = ∑ j = 1 s n l ( δ j ( n l ) ⋅ W j i n l − 1 ⋅ f ′ ( z i n l − 1 ) ) = ( ∑ j = 1 s n l δ j ( n l ) ⋅ W j i n l − 1 ) ⋅ f ′ ( z i n l − 1 )
因此有:
δ(l)i=(∑j=1sl+1δ(l+1)j⋅W(l)ji)⋅f′(z(l)i) δ i ( l ) = ( ∑ j = 1 s l + 1 δ j ( l + 1 ) ⋅ W j i ( l ) ) ⋅ f ′ ( z i ( l ) )
对于神经网络中的权重和偏置的更新公式为:
∂∂W(l)ijJ(W,b;x,y)=a(l)jδ(l+1)i ∂ ∂ W i j ( l ) J ( W , b ; x , y ) = a j ( l ) δ i ( l + 1 )
∂∂b(l)iJ(W,b;x,y)=δ(l+1)i ∂ ∂ b i ( l ) J ( W , b ; x , y ) = δ i ( l + 1 )
2.6、神经网络的学习过程
对于神经网络的学过程,大致分为如下的几步:
- 初始化参数,包括权重、偏置、网络层结构,激活函数等等
- 循环计算
- 返回最终的神经网络模型
参考文献
1、英文版:UFLDL Tutorial
2、中文版:UFLDL教程

