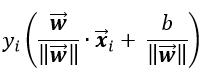机器学习笔记之（5）——SVM分类器
本博客为SVM分类器的学习笔记~由于仅仅是自学的笔记，大部分内容来自参考书籍以及个人理解，还请广大读者多多赐教
主要参考资料如下：
- 《机器学习实战》
- 《Python机器学习》
- 《机器学习Python实践》
- 《Python机器学习算法》
- 《Python大战机器学习》
- 《Python与机器学习实战》
支持向量机（support vector machine，SVM）的基本模型是定义在特征空间上间隔最大的线性分类器。是一种二分类模型，当采用了核技巧后，支持向量机就可以用于非线性分类。
超平面——分类的决策边界。在SVM中，希望找到离分隔超平面最近的点（称为支持向量），确保它们离分隔超平面的距离尽可能的远。通过最大化支持向量到分隔超平面的距离来训练SVM。
SVM主要分为以下三类：
- 线性可分支持向量机（也称为硬间隔支持向量机）：当训练数据线性可分时，通过硬间隔最大化，学得一个线性可分支持向量机。
- 线性支持向量机（也称为软间隔支持向量机）：当训练数据近似线性可分时，通过软间隔最大化，学得一个线性支持向量机。
- 非线性支持向量机：当训练数据不可分时，通过使用核技巧以及软间隔最大化，学得一个非线性支持向量机。
SVM本质上是非线性方法。
线性可分支持向量机：
在SVM中，优化的目标是最大化分类间隔，此处间隔是指两个分离的超平面（决策边界）间的距离，而最靠近超平面的训练样本陈作支持向量。而支持向量正是对最大间隔分离超平面起到确定性作用，这也是支持向量机名称的由来。
当训练集数据线性可分时，理论上存在无穷多个超平面可以将数据划分，而线性可分支持向量机就提出了分类间隔最大化这个约束，使得最终求得的超平面只有一个（如上图所示）。决策边界间具有较大的间隔意味着模型具有较小的泛化误差，而较小的间隔则意味着模型可能过拟合。
超平面可以用方程表示：
对于线性可分支持向量机，通常可以将一个样本距离分离超平面的远近来表示分类预测的可靠程度：一个样本距离分离超平面越远，则该样本的分类越可靠；一个样本距离分离超平面越远，则该样本的分类越可靠；一个样本距离分离超平面越近，则该样本的分类就不那么确信。
对于给定的超平面，样本
距离超平面的距离为：
。
，分类为正类，样本位于超平面上方。若
也为正类，则分类正确。
，分类为负类，样本位于超平面下方。若也为负类，则分类正确。
故此可以用
来表示分类的正确性以及确信度（符号正负决定了分类正确性，范数决定了确信度）。故此，对于给定训练数据集T，给定超平面
，定义超平面
关于训练样本点
的函数间隔为：
这个函数间隔存在一个重要的缺陷：当成比例地改变
，函数间隔也成比例改变，为此引入几何间隔：
定义超平面关于训练集T的几何间隔为超平面关于T中所有样本点的几何间隔之最小值：
注意，
为训练集与超平面的间隔，等于训练集中样本与超平面间隔
的最小。
而支持向量机的判别准则是：最大化分类间隔，也就是几个间隔最大的分离超平面。（此处的几何间隔最大化就是上面说到的硬 间隔最大化）
且有：
训练样本i集与超平面的间隔为，而训练样本距超平面距离最小的，为这个训练集与超平面的距离，所以上面第二条公式成立。根据几何间隔与函数间隔的关系，上述关系转换为：
下面直接给出书本的照片：
补充一下上面所提到的函数间隔和几何间隔：
一般来说，一个样本点距离分隔超平面的远近可以表示分类预测的确信程度。在下图中，样本点A离分隔超平面最远，若预测其为正类，就比较确信该预测是正确的；而C样本点离分隔超平面比较近，若预测其为正类，则没有A那么确信。为了表征分类预测的确信程度，定义函数间隔和几何间隔。
函数间隔：
对于在超平面
下，样本点i，可以表示为样本点i距离超平面的远近。当
与样本点i的标签
同号时，表明分类正确，所以可以使用
来表示分类的正确性和置信度，这就是函数间隔的定义。同时，定义分隔超平面关于训练数据集的函数间隔为分隔超平面关于训练数据集中所有样本点的函数间隔的最小值：
函数间隔可以表示分类预测的正确性和确定性。但是，在分隔超平面中，如果其参数同时扩大2倍，对于分隔超平面来说没有任何变化，但是对于函数间隔
来说就扩大为原来的两倍，所以引入几何间隔：
为了能使间隔是一个确定的值，可以对分隔超平面的参数W进行归一化，则样本点i到分隔超平面的距离为：
同样是当与i的标签同号时预测正确，则几何间隔定义为：
同时定义分隔超平面关于训练数据集的几何间隔为：
且有：
而支持向量机则是要通过训练集，求几何间隔最大的分隔超平面：
同时，对于每一个样本，需要满足：
同时，考虑到几何间隔和函数间隔之间的关系，上述两式等价为
下面给出Python代码：
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets,linear_model,cross_validation,svm
###############################################################################
#做分类时的数据
def load_data_classfication():
iris=datasets.load_iris()#采用的是莺尾花数据集
return cross_validation.train_test_split(iris.data,iris.target,test_size=0.25,random_state=0)
#之所以要采用分层采样，原因是原始数据集中，前50个样本都是类别0，中间50个样本都是类别1，最后50个样本都是类别2
#如果不采用分层采样，那么最后切分得到的测试数据集就不是无偏的了。
###############################################################################
#线性分类SVM
def test_LinearSVC(*data):
x_train,x_test,y_train,y_test=data
cls=svm.LinearSVC()
cls.fit(x_train,y_train)
print('线性分类SVM')
print('Coefficients:%s, intercept %s'%(cls.coef_,cls.intercept_))
print('Score: %.2f' % cls.score(x_test, y_test))
###############################################################################
#考察损失函数的影响，不同的损失函数对分类性能的影响
def test_LinearSVC_loss(*data):
x_train,x_test,y_train,y_test=data
losses=['hinge','squared_hinge']
for loss in losses:
cls=svm.LinearSVC(loss=loss)
cls.fit(x_train,y_train)
print('考察损失函数的影响')
print("Loss:%s"%loss)
print('Coefficients:%s, intercept %s'%(cls.coef_,cls.intercept_))
print('Score: %.2f' % cls.score(x_test, y_test))
###############################################################################
#考察惩罚形式的影响
def test_LinearSVC_L12(*data):
x_train,x_test,y_train,y_test=data
L12=['l1','l2']
for l in L12:
cls=svm.LinearSVC(penalty=l,dual=False)
cls.fit(x_train,y_train)
print('考察惩罚形式的影响')
print("Loss:%s"%l)
print('Coefficients:%s, intercept %s'%(cls.coef_,cls.intercept_))
print('Score: %.2f' % cls.score(x_test, y_test))
###############################################################################
#考察惩罚项系数C的影响。C衡量了误分类点的重要性，C越大则误分类点越重要。
def test_LinearSVC_C(*data):
x_train,x_test,y_train,y_test=data
Cs=np.logspace(-2,1)#创建等比数列,np.logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None);
#第一个数为10的-2次方，即0.01，见后面注释。
train_scores=[]
test_scores=[]
for C in Cs:
cls=svm.LinearSVC(C=C)
cls.fit(x_train,y_train)
train_scores.append(cls.score(x_train,y_train))
test_scores.append(cls.score(x_test,y_test))
#绘图
fig=plt.figure()
ax=fig.add_subplot(1,1,1)
ax.plot(Cs,train_scores,label="train score")
ax.plot(Cs,test_scores,label="tset score")
ax.set_xlabel("C")
ax.set_ylabel("score")
ax.set_xscale('log')
ax.set_title("线性SVC")
ax.legend(loc='best')
plt.show()
###############################################################################
#测试
x_train,x_test,y_train,y_test=load_data_classfication()
test_LinearSVC(x_train,x_test,y_train,y_test)
test_LinearSVC_loss(x_train,x_test,y_train,y_test)
test_LinearSVC_L12(x_train,x_test,y_train,y_test)
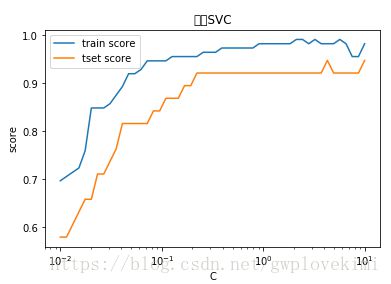
test_LinearSVC_C(x_train,x_test,y_train,y_test)结果如下图所示：
从图中可以看出，当惩罚项系数C较小时，误分类点的重要性较低，此时误分类点较多，分类器性能较差。
对于上面程序补充如下：
Cs=np.logspace(-2,1)#创建等比数列,np.logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None);
感觉Python太多函数太多库了，然后本人都不是特别的熟悉，所以经常要百度翻书，大概也是用得太少了吧。对于Python各种常用的库及其函数可以参考书籍《Python科学计算》
线性分类SVM为SVC，线性回归SVM为SVR，下面给出线性回归SVM代码：
from sklearn import datasets,cross_validation,svm
###############################################################################
#做回归时的数据
def load_data_regression():
diabetes=datasets.load_diabetes()#采用scikit-learn中的糖尿病病人的数据集
return cross_validation.train_test_split(diabetes.data,diabetes.target,test_size=0.25,random_state=0)
#return: 一个元组，用于分类问题。元组元素依次为：训练样本集、测试样本集、训练样本集对应的标记、测试样本集对应的标记
###############################################################################
#线性回归SVM
def test_LinearSVR(*data):
x_train,x_test,y_train,y_test=data
regr=svm.LinearSVR()
regr.fit(x_train,y_train)
print('Coefficients:%s, intercept %s'%(regr.coef_,regr.intercept_))
print('Score: %.2f' % regr.score(x_test, y_test))
###############################################################################
x_train,x_test,y_train,y_test=load_data_regression()
test_LinearSVR(x_train,x_test,y_train,y_test)程序结果如下图所示：
线性支持向量机：
使用松弛变量解决非线性可分的问题。通过引入松弛变量，使得对于非线性可分的数据在保证适当的惩罚成本的作用下，对非线性可分的数据进行线性分类。其实就是允许一定容错率的情况下，来对非线性可分数据继续线性分类。
下面给出《Python大战机器学习》一书中理论部分的截图：
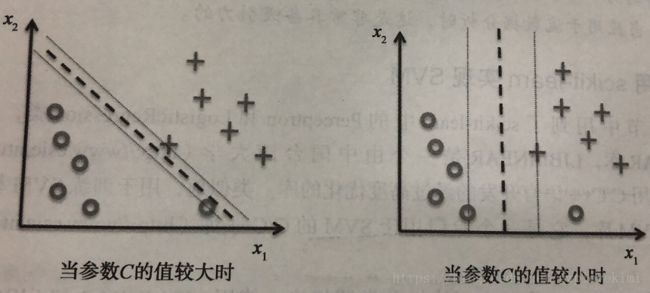
通过控制图中的变量C可以控制对错误分类的惩罚程度。C值较大时，对应大的错误惩罚。这样分类测试的效果会更好（参见上面 程序惩罚系数与分类器性能的图。在前面博客机器学习笔记（3）中，对正则化做过讨论，增加C值，会增加偏差但同时也会降低模型的方差，而过拟合就是高方差导致的，欠拟合是高偏差导致的，可以通过使用参数C来控制间隔的大小，进而可以在偏差和方差之间取得平衡，如下图所示：
非线性支持向量机：
SVM在机器学习中广受欢迎的一个原因是：它可以使用“核技巧”来解决非线性可分的问题。核方法处理非线性可分数据的基本理念是：通过映射函数将样本的原始特征映射到一个使样本线性可分的更高维空间（如下图所示）。
从而可以使用线性超平面进行分割，再把这超平面映射回原始的特征空间。常见的核函数有：径向基函数核、多项式核、高斯核和sigmoid核等。
给出python代码如下：
在sklearn.svm.SVC中实现了非线性SVM，当非线性SVM采用线性核时与线性SVM（sklearn.svm.LinearSVC）的对比如下：
from sklearn import datasets,cross_validation,svm
###############################################################################
#做分类时的数据
def load_data_classfication():
iris=datasets.load_iris()#采用的是莺尾花数据集
return cross_validation.train_test_split(iris.data,iris.target,test_size=0.25,random_state=0)
#之所以要采用分层采样，原因是原始数据集中，前50个样本都是类别0，中间50个样本都是类别1，最后50个样本都是类别2
#如果不采用分层采样，那么最后切分得到的测试数据集就不是无偏的了。
###############################################################################
#线性分类SVM
def test_LinearSVC(*data):
x_train,x_test,y_train,y_test=data
cls=svm.LinearSVC()
cls.fit(x_train,y_train)
print('线性分类SVM')
print('Coefficients:%s, intercept %s'%(cls.coef_,cls.intercept_))
print('Score: %.2f' % cls.score(x_test, y_test))
###############################################################################
#非线性分类SVM采用线性核
def test_SVC_Linear(*data):
x_train,x_test,y_train,y_test=data
cls=svm.SVC(kernel='linear')
cls.fit(x_train,y_train)
print('非线性分类SVM采用线性核')
print('Coefficients:%s, intercept %s'%(cls.coef_,cls.intercept_))
print('Score: %.2f' % cls.score(x_test, y_test))
###############################################################################
#测试
x_train,x_test,y_train,y_test=load_data_classfication()
test_LinearSVC(x_train,x_test,y_train,y_test)
test_SVC_Linear(x_train,x_test,y_train,y_test)结果如下图所示：
可以看出，非线性SVM采用线性核的预测效果比线性SVM的预测效果更好。在《Python大战机器学习》一书中，还有关于多项式核、高斯核和sigmoid核的分析，此处不一一列出来，有兴趣的读者请直接看吧
下面给出非线性回归SVR线性核的代码并与线性回归SVR进行对比：
from sklearn import datasets,cross_validation,svm
###############################################################################
#做回归时的数据
def load_data_regression():
diabetes=datasets.load_diabetes()#采用scikit-learn中的糖尿病病人的数据集
return cross_validation.train_test_split(diabetes.data,diabetes.target,test_size=0.25,random_state=0)
#return: 一个元组，用于分类问题。元组元素依次为：训练样本集、测试样本集、训练样本集对应的标记、测试样本集对应的标记
###############################################################################
#线性回归SVM
def test_LinearSVR(*data):
x_train,x_test,y_train,y_test=data
regr=svm.LinearSVR()
regr.fit(x_train,y_train)
print('Coefficients:%s, intercept %s'%(regr.coef_,regr.intercept_))
print('Score: %.2f' % regr.score(x_test, y_test))
###############################################################################
#非线性回归SVM线性核
def test_SVR_Linear(*data):
x_train,x_test,y_train,y_test=data
regr=svm.SVR(kernel='linear')
regr.fit(x_train,y_train)
print('Coefficients:%s, intercept %s'%(regr.coef_,regr.intercept_))
print('Score: %.2f' % regr.score(x_test, y_test))
###############################################################################
x_train,x_test,y_train,y_test=load_data_regression()
test_LinearSVR(x_train,x_test,y_train,y_test)
test_SVR_Linear(x_train,x_test,y_train,y_test)结果如下图所示：
同样可以看出，非线性回归SVR的线性核效果比线性回归SVR要好。
补充：在实际的分类任务中，逻辑斯蒂回归与SVM往往能得到非常相似的结果。逻辑斯蒂回归会尽量最大化训练数据集的条件似然，比SVM更容易处理离散点群。而SVM则更关注接近决策边界（支持向量）的点。
好~SVM的学习笔记到此结束。感觉本节对于理论部分理解不是特别清晰，在sklearn中直接用函数其实真的是比较方便，但后续有新的体会以及深入理解数学推导后，会继续更新本博客~谢谢