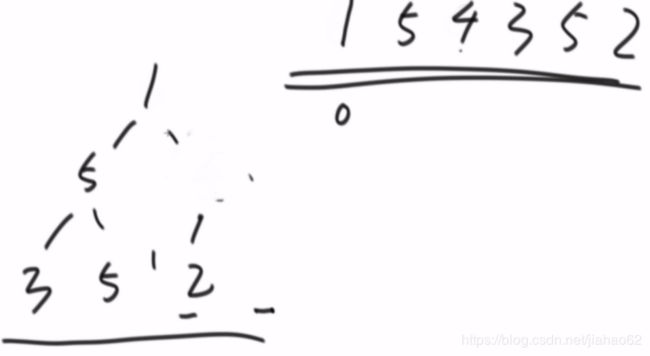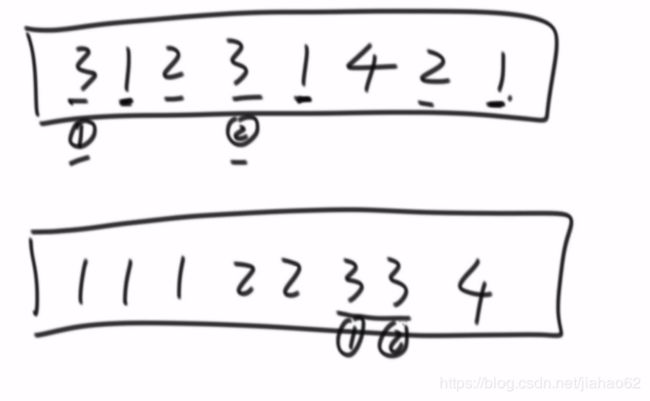算法基础--第二章--认识O(N*logN)的排序
--归并排序详解
--快速排序详解
--堆结构和堆排序详解
问题一·(荷兰国旗问题)
给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,大于num的数放在数组的右边。
要求额外空间复杂度O(1),时间复杂度O(N)
问题二·(荷兰国旗问题)
给定一个数组arr,和一个数num,请把小于num的数放在数组的左边,等于num的数放在数组的中间,大于num的数放在数组的
右边。
要求额外空间复杂度O(1),时间复杂度O(N)
public static int[] partition(int[] arr, int l, int r, int p) {
int less = l - 1;
int more = r + 1;
while (l < more) {
if (arr[l] < p) {
swap(arr, ++less, l++);
} else if (arr[l] > p) {
swap(arr, --more, l);
} else {
l++;
}
}
return new int[] { less + 1, more - 1 };
}
快速排序
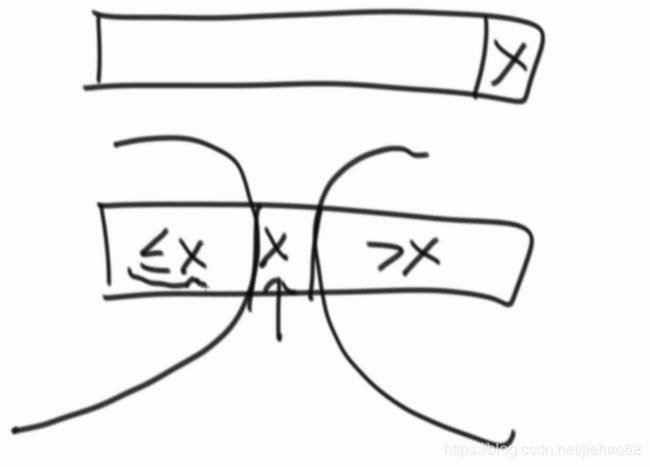
经典快速排序的基本思想是
1、先从数列中取出一个数作为基准数
2、分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边
3、再对左右区间重复第二步,直到各区间只有一个数
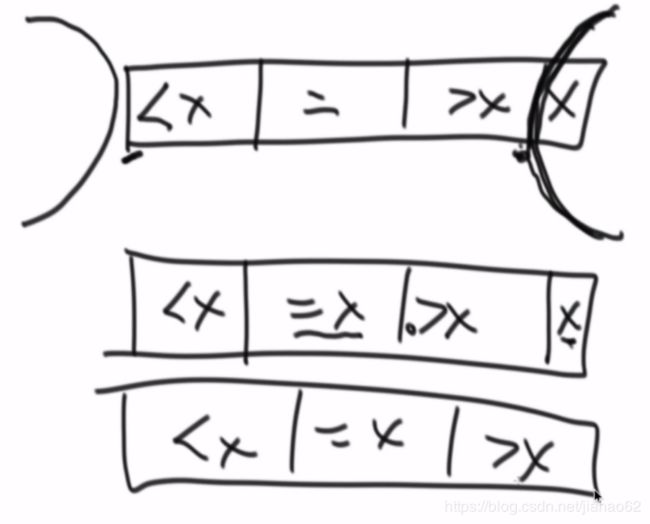
结合荷兰国旗思想后的改进快排(等于区域直接划好):
public class Code_04_QuickSort {
public static void quickSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
quickSort(arr, 0, arr.length - 1);
}
public static void quickSort(int[] arr, int l, int r) {
if (l < r) {
swap(arr, l + (int) (Math.random() * (r - l + 1)), r); //随机快排
int[] p = partition(arr, l, r);
quickSort(arr, l, p[0] - 1);
quickSort(arr, p[1] + 1, r);
}
}
public static int[] partition(int[] arr, int l, int r) {
int less = l - 1;
int more = r;
while (l < more) {
if (arr[l] < arr[r]) {
swap(arr, ++less, l++);
} else if (arr[l] > arr[r]) {
swap(arr, --more, l);
} else {
l++;
}
}
swap(arr, more, r);
return new int[] { less + 1, more };
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
partition(处理边界条件):
随机快排:
经典快排存在的问题:有序下每次只能搞定一个数![]()
最理想在中间:T(N)=2T(N/2) +O(N)
随机选一个数,和最后一个交换,再进行快排。 长期期望:O(N*logN),额外空间复杂度O(logN) 断点
绕开原始数据状况 1)随机 2)哈希
堆排序
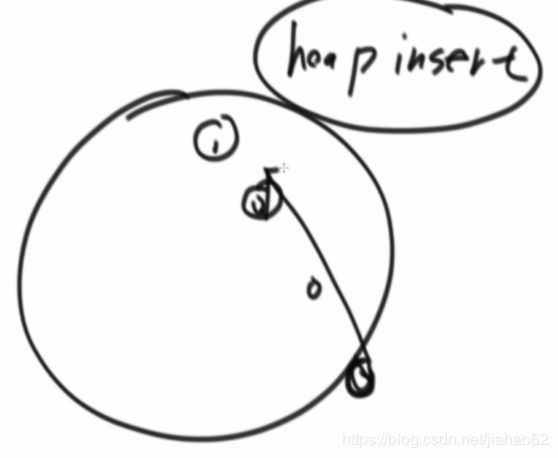
1,堆结构的heapInsert与heapify
2,堆结构的增大和减少
3,如果只是建立堆的过程,时间复杂度为O(N)
4,优先级队列结构,就是堆结构
时间复杂度O(N*logN),额外空间复杂度O(1)
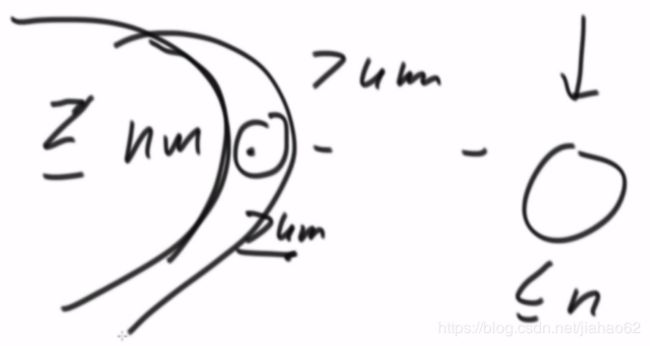
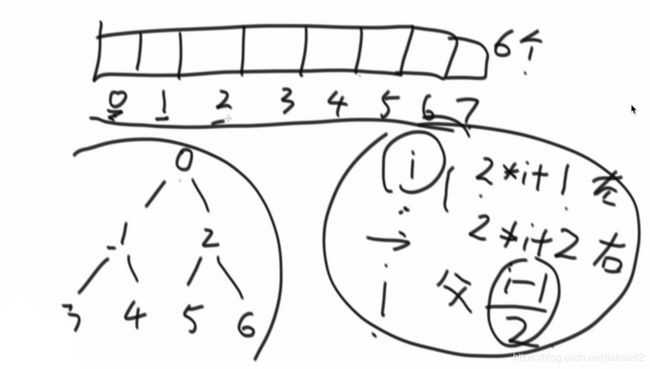
数组 - 二叉树
堆:大(小)根堆 -- 完全二叉树 任何一个子树的最大(小)值都是头部。
数组 -> 大根堆
heapInsert:新进来的找父节点如果大然后交换
public static void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length; i++) {
heapInsert(arr, i);
}
int size = arr.length;
swap(arr, 0, --size);
while (size > 0) {
heapify(arr, 0, size);
swap(arr, 0, --size);
}
}
public static void heapInsert(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
public static void heapify(int[] arr, int index, int size) {
int left = index * 2 + 1;
while (left < size) {
int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
swap(arr, largest, index);
index = largest;
left = index * 2 + 1;
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
堆一个数字变化进行调整 heapify 下沉
流不断吐出数,求中位数:大根堆,小根堆保持一个平衡(差值大于1)
堆上弹出堆顶:最后一个数站在堆顶的位置,把标记越界的变量减1,从0位置经历一个heapify恢复大根堆。
堆排序:1) 形成大根堆 ->最后一个位置与堆顶位置交换 ,堆减一,重新调整堆。
排序算法的稳定性及其汇总
稳定性:相对位置不变(多维度,保留了先前的信息)
不变:冒泡,插入,归并
变化:选择, 快排(随机),堆排序。