经典排序算法3：堆排序

本文根据算法导论第6章，介绍最大堆的操作。包括：构建最大堆，维护最大堆，堆排序，以及对在优先队列中的应用。对最大优先队列执行以下操作：向队列中插入新元素，增加某个元素的值，去掉并返回队列中的最大值并保证最大队的性质。
首先定义满二叉树：
一棵深度为 k 且有 2k−1 的二叉树，即每个节点是叶节点或者度为2.
如下图是一棵深度为满二叉树：

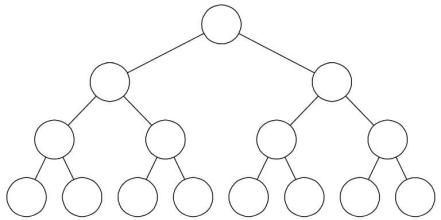
对满二叉树的节点进行编号，约定编号从很节点起，自上而下，自左向右。深度为 k 的有 n 个节点的二叉树，当且仅当其每一个节点都与深度为 k 的满二叉树编号从1至 n 的节点一一对应，则称为完全二叉树。
如下图是深度为4的完全二叉树

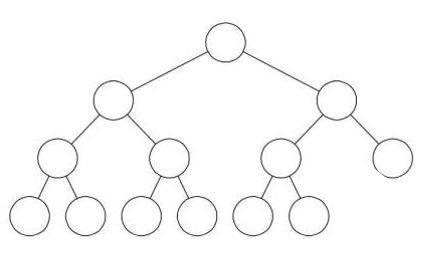
若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层从右向左连续缺若干结点，这就是完全二叉树。

二叉堆 是一个数组数组，也可以看成一棵完全二叉树或者近似完全二叉树，将完全二叉树从左到右，从上到下依次编号，即对应数组中的元素。
本文只介绍二叉堆中的最大堆，下文默认二叉堆为最大堆。
如图分别是二叉堆的数组表示和完全二叉树表示：

一个包含 n 个元素的二叉堆看成一个完全二叉树，树的高度为 H=⌊log2n⌋+1 , (将只有一个根节点的情况看作高度为1)。
最大堆的性质：除了叶子节点外，所有父节点均大于孩子节点
A[i]≥A[leftChild(i)]
A[i]≥A[rightChild(i)]
最大堆的最大元素存于根节点，即数组的第一个元素 A[0] 。
下面介绍二叉堆的基本操作：
1.二叉堆的维护
一个节点 A[i] 的左子树和右子树都是最大堆，但是以 A[i] 为根节点的完全二叉树未必构成最大堆，因为条件 A[i]≥A[leftChild(i)]且A[i]≥A[rightChild(i)] 不一定满足，因此要维护最大堆的性质。
当 A[i]<A[leftChild(i)] 或者 A[i]<A[rightChild(i)] 时， A[i] 要和 max{A[leftChild(i)],A[rightChild(i)]} 交换，将原来的根节点 A[i] 往下移。假设 A[i] 和 做左孩子 A[leftChild(i)] 交换，可能导致新二叉树中以 A[leftChild(i)] 为根节点的二叉树不满足最大堆的性质。
依次类推，将问题沿着二叉树往下移，直到条件 A[i]≥A[leftChild(i)]且A[i]≥A[rightChild(i)] 成立。

伪代码：

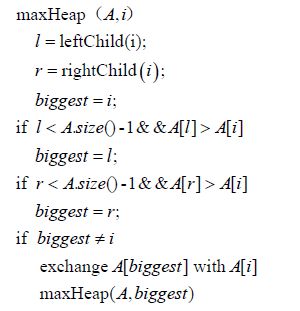
时间复杂度：
由于递归调用 maxHeap(vector &vec, int p) 的次数最多等于二叉树的高度 h , 当要交换根节点 A[i] 与 其某个孩子节点时，时间代价为 Θ(1) , 即 maxHeap 的时间复杂度为 O(h) , 即 O(log2n) 。

2.构建最大堆
将一个无序排列的完全二叉树 A进行改造，构造最大堆。
首先，所有叶子节点都可以看成最大堆，而所有非叶子节点都要进行改造，最后一个非叶子节点也就是最后也就是一个叶子节点的父亲节点 A[parent(A.size()−1)] 。
从节点 A[parent(A.size()−1)] 开始，自底向上，自右向左，直到 A[0] ,依次调用 maxHeap。即先将下面的子树维护成最大堆，再各个子树的父亲节点是否满足最大堆性质，依次向上进行最大堆维护操作，即将问题向上移动，最后整个二叉树即构成最大堆。
伪代码：

时间复杂度：
对不同的节点维护最大堆的性质，运行 maxHeap，时间代价与这个节点的高度相关。完全二叉树节点为 n ,（设最底层的叶子节点的高度为1）， 高度为 h 的节点数目为最多为 ⌈n/2h⌉ , 在高度为 h 的节点上运行 maxHeap 的时间代价为 O(h) , 则总的时间代价可以表示为：
∑H1⌈n/2h⌉O(h)=O(n∑⌊log2n⌋+11h2h)=O(n)

3.堆排序
堆排序的基本原理：
由最大堆的性质，最大堆的根元素（也就是第一个元素数组）即为最大元素，将根元素的取出保存，并将此二叉树的最后一个叶子节点移到根位置，替换已有的根元素。这时，整棵二叉树size 减1，根元素的左右子树一定满足对大堆的性质，但是整个二叉树不一定满足最大堆的性质，因此要对根元素执行最大堆的维护，运行 maxHeap 。当整棵二叉树重新满足最大堆的性质后，在做同样的操作，即将根元素的取出保存……直到最后新的二叉树只剩下一个元素，这一个元素即为当前新树的最大元素，直接取出。
按照一个个根元素从树上被取出的先后顺序，将其进行排序，即可得到数值上的有序序列。
下述子函数 void buildHeap(vector & vec) 已经叙述得清晰明了，不再赘述伪代码。
时间复杂度分析：
运行 buildHeap 的时间代价为 O(n) , 另外 运行 n−1 次 maxHeap，每次为 O(log2n） , 即总的时间代价为 O(nlog2n)
上述时间的复杂度是算法导论上写的。
但是本人觉得这个上界可以更紧，
调用的 maxHeapify (A,1)， n-1 次， 但是每次时间代价并不都是 O(H) ,而是 H−h ，因为这颗完全二叉树的 size 在不断减小（最大元素的值保存并删除，用最后的叶子节点代替），所以根据最初的二叉树第 h 层 (最底层为第1 层)的元素个数 为 ⌈n/2h⌉ ，推到过程如下：其中 H=⌊log2n⌋+1
∑H−11⌈n/2h⌉(H−h)=(⌊log2n⌋+1)n∑H−11⌈1/2h⌉−n∑H−11⌈h/2h⌉<nlog2n+n(∑H−11⌈1/2h⌉−∑H−11⌈h/2h)<nlog2n
所以推导了一遍，还是书上写的 O(nlog2n) 。
堆排序是不稳定的排序方式，最大堆的最后两个叶子节点相等，最后一个叶子被移到根位置，然后往下移动，最后很可能不再试最后一个元素了。

接下来介绍，堆排序在优先队列中的应用：
1. increaceHeap（A,loc,newValue），将某个元素 A[loc] 的键值增大到 newKey，即相当于提升优先级，
由于将元素 A[loc] 的值增大后，A[loc] 的左右子树依旧满足最大堆性质，但是从 A[loc]的值如果大于其 父亲节点 A[parent(loc)]，则必须交换 A[loc]，和 A[parent(loc)]，将较大的数值 newKey 往上挪，每挪到一个位置，这个位置的左右子树都满足最大堆性质，但是这个 newKey 所在的节点可能仍旧大于 该节点的父亲，所以一直沿着父子关系往上移动，直到找到一个合适的位置，这是 newKey 所在的节点不大于该节点的父亲。即达到目的。
时间复杂度为 O(log2n) 。
2. insertHeap(A, newValue)插入新元素
首先在二叉树的末尾添加一个键值无穷小的新元素，运行increaceHeap，相当于将最后一个叶子数值增加
到 newValue。
时间复杂度为 O(log2n) 。
3. extratMaxHeap(A, heapSize)
返回最大堆中的最大数，即根元素，并去掉根元素，然后重新调整成最大堆。
时间复杂度为 O(log2n) 。

C++ 代码

const int infmin = -1000;
int parent(int i)
{
    return (i + 1) / 2 - 1;
}
int leftChild(int i)
{
    return (i + 1) * 2 - 1;
}
int rightChild(int i)
{
    return (i + 1) * 2;
}

void maxHeap(vector<int> &vec, int heapSize, int p)
{
    int pValue = vec[p];
    int largestLoc = p;
    //int vecSize = vec.size();
    if (leftChild(p) <= heapSize - 1 && vec[leftChild(p)] > vec[largestLoc])
    {
        largestLoc = leftChild(p);
    }
    if (rightChild(p) <= heapSize - 1 && vec[rightChild(p)] > vec[largestLoc])
    {
        largestLoc = rightChild(p);
    }
    if (largestLoc != p)
    {
        swap(vec[largestLoc], vec[p]);
        maxHeap(vec,heapSize, largestLoc);
    }
}
void buildHeap(vector<int> & vec)
{
    int vecSize = vec.size();
    // 从最后一个叶节点的的父亲节点开始，因为它是最后一个有孩子的节点
    int lastParent = parent(vecSize - 1);
    for (int p = lastParent; p >= 0; p--)
    {
        maxHeap(vec, vecSize,p);
    }
}

void heapSort(vector<int> & vec)
{
    int heapSize = vec.size();
    //第一步，建立最大堆
    buildHeap(vec);
    //每次把最大的元素拿出来，然后重新维护最大堆
    while (heapSize >= 2)
    {
        swap(vec[0], vec[heapSize - 1]);
        heapSize--;
        maxHeap(vec, heapSize, 0);
    }
}
void increaceHeap(vector<int> &heap, int loc, int newValue)
{
    if (heap[loc] >= newValue)
    {
        cout << "NewValue must be bigger than the original value! " << endl;
    }
    else
    {
        heap[loc] = newValue;
        int p = parent(loc);
        while (p >= 0 && heap[p] < heap[loc])
        {
            swap(heap[p], heap[loc]);
            loc = p;
            p = parent(p);
        }
    }
}
void insertHeap(vector<int> &heap, int newValue)
{
    heap.push_back(infmin);
    increaceHeap(heap, heap.size() - 1, newValue);

}
int extratMaxHeap(vector<int>&vec,int heapSize)
{
    int max = vec[0];
    swap(vec[0], vec[heapSize - 1]);
    vec.pop_back();
    heapSize --;
    maxHeap(vec, heapSize, 0);
    return max;
}

排序方法的比较：
堆排序与 归归并排序的时间复杂度一样，都为 O(nlog2n) , 且只需要常数个额外的空间存储临时数据，具有和 插入排序一样的空间原址性的优点。即堆排序具备归并排序和插入排序的优点，但是堆排序不具有稳定性。