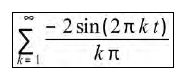Numpy（三）矩阵

1、矩阵的创建

(1) 在创建矩阵的专用字符串中，矩阵的行与行之间用分号隔开，行内的元素之间用空格隔开。

(2) 用T属性获取转置矩阵

mat函数创建

import numpy as np
A=np.mat('1 2 3;4 5 6;7 8 9')
print A
print A.T
print np.mat(np.arange(24)).reshape(6,4)

单位矩阵：

A = np.eye(2)
print "A", A

使用字符串创建复合矩阵，该字符串的格式与mat函数中一致，只是在这里可以用矩阵变量名代替数字：

import numpy as np
A=np.eye(3)
print A
B=A*2
print B
print np.bmat('A B;A B')

2、运算

zeros_like（a）函数创建一个和a形状相同，并且元素全部为0的数组。

对于add函数，其对数组的reduce计算结果等价于对数组元素求和

accumulate方法同样可以递归作用于输入数组。但是与reduce方法不同的是，它将存储运算的中间结果并返回。因此在add函数上调用accumulate方法，等价于直接调用cumsum函数。

outer方法返回一个数组，它的秩（rank）等于两个输入数组的秩的和。

import numpy as np
a=np.arange(9)
print np.add.reduce(a)
print np.add.accumulate(a)
# 实际上就是对数组中索引值在0到5之间的元素进行reduce操作。
#第二步用到索引值5和2。由于2比5小，所以直接返回索引值为5的元素
# 第四步用到索引值7。这一步是对索引值从7开始直到数组末端的元素进行reduce操作
print np.add.reduceat(a,[0,5,2,7])
print np.add.outer(np.arange(6),a)

divide函数在整数和浮点数除法中均只保留整数部分

true_divide函数与数学中的除法定义更为接近，即返回除法的浮点数结果而不作截断

floor_divide函数总是返回整数结果，相当于先调用divide函数再调用floor函数。floor函数将对浮点数进行向下取整并返回整数

默认情况下，使用/运算符相当于调用divide函数

运算符//对应于floor_divide函数。

import numpy as np
a = np.array([2, 6, 5])
b = np.array([1, 2, 3])
print "Divide", np.divide(a, b), np.divide(b, a)
print "True Divide", np.true_divide(a, b), np.true_divide(b, a)
print "Floor Divide", np.floor_divide(a, b), np.floor_divide(b, a)
c = 3.14 * b
print "Floor Divide 2", np.floor_divide(c, b), np.floor_divide(b, c)
print "/ operator", a/b, b/a
print "// operator", a//b, b//a
print "// operator 2", c//b, b//c

remainder函数逐个返回两个数组中元素相除后的 余数。如果第二个数字为0，则直接返回0

mod函数与remainder函数的功能完全一致

%操作符仅仅是remainder函数的简写

fmod函数处理负数的方式与remainder、mod和%不同。所得余数的正负由被除数决定，与除数的正负无关

import numpy as np
a = np.arange(-4, 4)
print "Remainder", np.remainder(a, 2)
print "Mod", np.mod(a, 2)
print "% operator", a % 2
print "Fmod", np.fmod(a, 2)

3、斐波那契数列

斐波那契数列的计算等价于矩阵的连乘。

import numpy as np
# (1) 创建斐波那契矩阵
F = np.matrix([[1, 1], [1, 0]])
print "F", F
#(2) 计算斐波那契数列中的第8个数，即矩阵的幂为8减去1。计算出的斐波那契数位于矩阵的对角线上：
print "8th Fibonacci", (F ** 7)[0, 0]
# (3) 利用黄金分割公式或通常所说的比奈公式（Binet’ s Formula），加上取整函数，就可以直接计算斐波那契数。
n = np.arange(1, 9)
sqrt5 = np.sqrt(5)
phi = (1 + sqrt5)/2
fibonacci = np.rint((phi**n - (-1/phi)**n)/sqrt5)
print "Fibonacci", fibonacci

4、绘制利萨茹曲线
利萨茹曲线由以下参数方程定义：
x = A sin(at + n/2)
y = B sin(bt)

import numpy as np
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
import sys
# (1) 使用linspace函数初始化变量t，即从-pi到pi上均匀分布的201个点
a = float(9)
b = float(8)
t = np.linspace(-np.pi, np.pi, 201)
# (2) 使用sin函数和NumPy常量pi计算变量x
x = np.sin(a * t + np.pi/2)
# (3) 使用sin函数计算变量y
y = np.sin(b * t)
plot(x, y)
show()

5、方波

import numpy as np
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
import sys
# (1) 我们从初始化t和k开始，并将函数值初始化为0
t = np.linspace(-np.pi, np.pi, 201)
k = np.arange(1, float(100))
k = 2 * k - 1
f = np.zeros_like(t)
# (2) 接下来，直接使用sin和sum函数进行计算：
for i in range(len(t)):
    f[i] = np.sum(np.sin(k * t[i])/k)
f = (4 / np.pi) * f
# (3) 绘制波形的代码和前面的教程中几乎一模一样
plot(t, f)
show()

6、锯齿波和三角波

函数：

import numpy as np
from matplotlib.pyplot import plot
from matplotlib.pyplot import show
import sys
# (1) 将函数值初始化为0
t = np.linspace(-np.pi, np.pi, 201)
k = np.arange(1, float(100))
f = np.zeros_like(t)
# (2) 直接使用sin和sum函数进行计算
for i in range(len(t)):
    f[i] = np.sum(np.sin(2 * np.pi * k * t[i])/k)
f = (-2 / np.pi) * f
# (3) 同时绘制锯齿波和三角波并不难，因为三角波函数的取值恰好是锯齿波函数值的绝对值。使用如下代码绘制波形
plot(t, f, lw=1.0)
plot(t, np.abs(f), lw=2.0)
show()

7、位运算与比较运算

    位操作函数可以在整数或整数数组的位上进行操作，它们都是通用函数。^、&、|、<<、>>等位操作符在NumPy中也有对应的部分，<、>、==等比较运算符也是如此。

   XOR或者^操作符。XOR操作符又被称为不等运算符，因此当两个操作数的符号不一致时，XOR操作的结果为负数。在NumPy中，^操作符对应于bitwise_xor函数，
<操作符对应于less函数。

   位与操作AND，&操作符对应于bitwise_and函数，==操作符对应于equal函数

计算余数的技巧实际上只在模为2的幂数（如4、8、16等）时有效。二进制的位左移一位，则数值翻倍。

import numpy as np
x = np.arange(-9, 9)
y = -x
print "Sign different?", (x ^ y) < 0
print "Sign different?", np.less(np.bitwise_xor(x, y), 0)
print "Power of 2?\n", x, "\n", (x & (x - 1)) == 0
print "Power of 2?\n", x, "\n", np.equal(np.bitwise_and(x, (x - 1)), 0)
print "Modulus 4\n", x, "\n", x & ((1 << 2) - 1)
print "Modulus 4\n", x, "\n", np.bitwise_and(x, np.left_shift(1, 2) - 1)