机器学习实战(六)——SVM
支持向量机
线性分类
分类标准
考虑二分类的问题,数据点用 x x 表示,这是一个 n n 维向量,类别用 y y 来表示,取值为-1或1(与Logistc相同), 分别代表两个不同的类。一个线性分类器的学习目标就是要在 n n 维的数据空间中找到一个分类超平面,其方程为:
wTx+b=0 w T x + b = 0
特别的,对于二维平面,超平面方程为
[a b][x1x2]+b=0 [ a b ] [ x 1 x 2 ] + b = 0
就是一个直线方程
ax1+bx2+b=0 a x 1 + b x 2 + b = 0
线性分类的例子
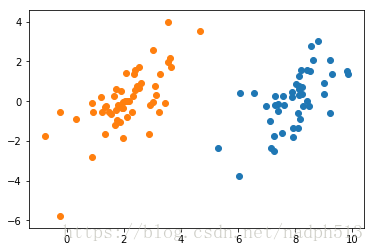
下面是一个简单的例子,一个二维平面 (一个超平面,在二维空间中的例子就是一条 直线),如下图所示,平面上有两种不同的点,分别用两种不同的颜色表示,一种为红 颜色的点,另一种则为蓝颜色的点,红颜色的线表示一个可行的超平面。
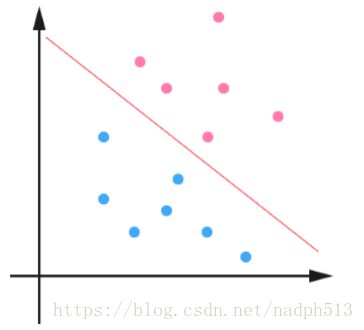
从上图中我们可以看出,这条红颜色的线把红颜色的点和蓝颜色的点分开来了。而 这条红颜色的线就是我们上面所说的超平面,也就是说,这个所谓的超平面的的确确便 把这两种不同颜色的数据点分隔开来,在超平面一边的数据点所对应的 y 全是−1 ,而 在另一边全是 1 。
令分类函数为:
f(x)=wTx+b f ( x ) = w T x + b
显然,如果 f(x)=0 f ( x ) = 0 ,那么 x x 是位于超平面上的点。我们不妨要求对于所有满足 f(x)<0 f ( x ) < 0 的点,其对应的 y y 等于−1 ,而 f(x)>0 f ( x ) > 0 则对应 y=1 y = 1 的数据点。
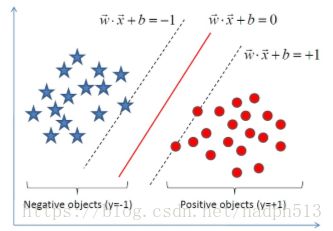
最大间隔分类器
点到直线的距离:
d=∣∣∣Ax0+By0+CA2+B2−−−−−−−√∣∣∣ d = | A x 0 + B y 0 + C A 2 + B 2 |
对于高维的超平面,显然也有:
d=|wTx+b|||w|| d = | w T x + b | | | w | |
显然,求解距离最大值就是求得的最好的分割超平面。
由于支持向量上的点满足
|wTx0+b|=1 | w T x 0 + b | = 1
因此优化目标可进一步化简为
d=1||w|| d = 1 | | w | |
综上:
min12||w||2 m i n 1 2 | | w | | 2
s.t. yi(wTxi+b)≥1 s . t . y i ( w T x i + b ) ≥ 1
KKT条件
一个最优化模型能够表示成下列标准形式:
mins.t. f(x)hj(x)=0gk(x)≤0 m i n f ( x ) s . t . h j ( x ) = 0 g k ( x ) ≤ 0
对于我们的优化问题,满足KKT条件。
SMO算法
SMO算法的工作原理是:每次循环中选择两个alpha进行优化处理。一旦找到了一对合适的alpha,那么就增大其中一个同时减小另一个。这里所谓的”合适”就是指两个alpha必须符合以下两个条件,条件之一就是两个alpha必须要在间隔边界之外,而且第二个条件则是这两个alpha还没有进进行过区间化处理或者不在边界上。
应用简化版SMO算法处理小规模数据集
pwd'D:\\Projects\\notebooks\\Machine Learning in Action\\documents\\4'
import matplotlib.pyplot as plt
import numpy as np
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
def showDataSet(dataMat, labelMat):
data_plus = []
data_minus = []
for i in range(len(dataMat)):
if labelMat[i] > 0:
data_plus.append(dataMat[i])
else:
data_minus.append(dataMat[i])
data_plus_np = np.array(data_plus)
data_minus_np = np.array(data_minus)
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1])
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1])
plt.show()
dataMat, labelMat = loadDataSet('testSet.txt')
showDataSet(dataMat, labelMat)from numpy import *
def selectJrand(i,m):
j=i #we want to select any J not equal to i
while (j==i):
j = int(random.uniform(0,m))
return j
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
b = 0; m,n = shape(dataMatrix)
alphas = mat(zeros((m,1)))
iter = 0
while (iter < maxIter):
alphaPairsChanged = 0
for i in range(m):
fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
Ei = fXi - float(labelMat[i])#if checks if an example violates KKT conditions
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
j = selectJrand(i,m)
fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
Ej = fXj - float(labelMat[j])
alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L==H: print("L==H"); continue
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
if eta >= 0: print("eta>=0"); continue
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
alphas[j] = clipAlpha(alphas[j],H,L)
if (abs(alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); continue
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#update i by the same amount as j
#the update is in the oppostie direction
b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]): b = b1
elif (0 < alphas[j]) and (C > alphas[j]): b = b2
else: b = (b1 + b2)/2.0
alphaPairsChanged += 1
print("iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
if (alphaPairsChanged == 0): iter += 1
else: iter = 0
print( "iteration number: %d"% iter )
return b,alphas
def showClassifer(dataMat, w, b):
data_plus = []
data_minus = []
for i in range(len(dataMat)):
if labelMat[i] > 0:
data_plus.append(dataMat[i])
else:
data_minus.append(dataMat[i])
data_plus_np = np.array(data_plus)
data_minus_np = np.array(data_minus)
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7)
x1 = max(dataMat)[0]
x2 = min(dataMat)[0]
a1, a2 = w
b = float(b)
a1 = float(a1[0])
a2 = float(a2[0])
y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
plt.plot([x1, x2], [y1, y2])
for i, alpha in enumerate(alphas):
if abs(alpha) > 0:
x, y = dataMat[i]
plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
plt.show()
def get_w(dataMat, labelMat, alphas):
alphas, dataMat, labelMat = np.array(alphas), np.array(dataMat), np.array(labelMat)
w = np.dot((np.tile(labelMat.reshape(1, -1).T, (1, 2)) * dataMat).T, alphas)
return w.tolist()
b,alphas = smoSimple(dataMat, labelMat, 0.6, 0.001, 40)
w = get_w(dataMat, labelMat, alphas)iter: 0 i:0, pairs changed 1
j not moving enough
L==H
j not moving enough
L==H
iter: 0 i:8, pairs changed 2
L==H
j not moving enough
iter: 0 i:23, pairs changed 3
j not moving enough
iteration number: 38
j not moving enough
j not moving enough
iteration number: 39
j not moving enough
j not moving enough
iteration number: 40
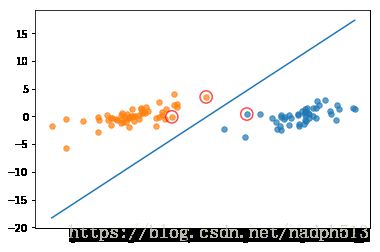
showClassifer(dataMat, w, b)完整版SMO算法
def kernelTrans(X, A, kTup): #calc the kernel or transform data to a higher dimensional space
m,n = shape(X)
K = mat(zeros((m,1)))
if kTup[0]=='lin': K = X * A.T #linear kernel
elif kTup[0]=='rbf':
for j in range(m):
deltaRow = X[j,:] - A
K[j] = deltaRow*deltaRow.T
K = exp(K/(-1*kTup[1]**2)) #divide in NumPy is element-wise not matrix like Matlab
else: raise NameError('Houston We Have a Problem -- \ That Kernel is not recognized')
return K
class optStruct:
def __init__(self,dataMatIn, classLabels, C, toler, kTup): # Initialize the structure with the parameters
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = shape(dataMatIn)[0]
self.alphas = mat(zeros((self.m,1)))
self.b = 0
self.eCache = mat(zeros((self.m,2))) #first column is valid flag
self.K = mat(zeros((self.m,self.m)))
for i in range(self.m):
self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
def calcEk(oS, k):
fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
def selectJ(i, oS, Ei): #this is the second choice -heurstic, and calcs Ej
maxK = -1; maxDeltaE = 0; Ej = 0
oS.eCache[i] = [1,Ei] #set valid #choose the alpha that gives the maximum delta E
validEcacheList = nonzero(oS.eCache[:,0].A)[0]
if (len(validEcacheList)) > 1:
for k in validEcacheList: #loop through valid Ecache values and find the one that maximizes delta E
if k == i: continue #don't calc for i, waste of time
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej
else: #in this case (first time around) we don't have any valid eCache values
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
def updateEk(oS, k):#after any alpha has changed update the new value in the cache
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]
def innerL(i, oS):
Ei = calcEk(oS, i)
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L==H: print("L==H"); return 0
eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel
if eta >= 0: print("eta>=0"); return 0
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
updateEk(oS, j) #added this for the Ecache
if (abs(oS.alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); return 0
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
updateEk(oS, i) #added this for the Ecache #the update is in the oppostie direction
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
else: oS.b = (b1 + b2)/2.0
return 1
else: return 0
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)): #full Platt SMO
oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
iter = 0
entireSet = True; alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet: #go over all
for i in range(oS.m):
alphaPairsChanged += innerL(i,oS)
print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
else:#go over non-bound (railed) alphas
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
if entireSet: entireSet = False #toggle entire set loop
elif (alphaPairsChanged == 0): entireSet = True
print("iteration number: %d" % iter)
return oS.b,oS.alphas
def calcWs(alphas,dataArr,classLabels):
X = mat(dataArr); labelMat = mat(classLabels).transpose()
m,n = shape(X)
w = zeros((n,1))
for i in range(m):
w += multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
def showClassifer(dataMat, classLabels, w, b):
data_plus = []
data_minus = []
for i in range(len(dataMat)):
if classLabels[i] > 0:
data_plus.append(dataMat[i])
else:
data_minus.append(dataMat[i])
data_plus_np = np.array(data_plus)
data_minus_np = np.array(data_minus)
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7)
x1 = max(dataMat)[0]
x2 = min(dataMat)[0]
a1, a2 = w
b = float(b)
a1 = float(a1[0])
a2 = float(a2[0])
y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
plt.plot([x1, x2], [y1, y2])
for i, alpha in enumerate(alphas):
if abs(alpha) > 0:
x, y = dataMat[i]
plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
plt.show()dataArr, classLabels = loadDataSet('testSet.txt')
b, alphas = smoP(dataArr, classLabels, 0.6, 0.001, 40)
w = calcWs(alphas,dataArr, classLabels)L==H
fullSet, iter: 0 i:0, pairs changed 0
L==H
fullSet, iter: 0 i:1, pairs changed 0
fullSet, iter: 0 i:2, pairs changed 1
L==H
fullSet, iter: 0 i:3, pairs changed 1
fullSet, iter: 0 i:4, pairs changed 2
fullSet, iter: 0 i:5, pairs changed 2
fullSet, iter: 0 i:6, pairs changed 2
j not moving enough
fullSet, iter: 0 i:7, pairs changed 2
L==H
fullSet, iter: 0 i:8, pairs changed 2
fullSet, iter: 0 i:9, pairs changed 2
L==H
fullSet, iter: 0 i:10, pairs changed 2
L==H
...
iteration number: 3
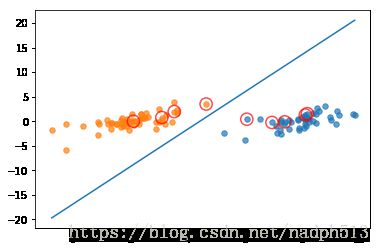
showClassifer(dataArr, classLabels, w, b)利用核函数处理线性不可分数据
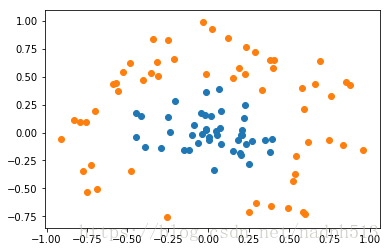
在线性不可分的情况下,SVM通过某种事先选择的非线性映射(核函数)将输入变量映到一个高维特征空间,将其变成在高维空间线性可分,在这个高维空间中构造最优分类超平面。
用通俗的话来说就是,看似不可区分的实体,同个增加特征,增加维数就能加以区分。
dataArr,labelArr = loadDataSet('testSetRBF.txt')
showDataSet(dataArr, labelArr)def testRbf(k1=1.3):
dataArr,labelArr = loadDataSet('testSetRBF.txt')
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 important
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
svInd=nonzero(alphas.A>0)[0]
sVs=datMat[svInd] #get matrix of only support vectors
labelSV = labelMat[svInd];
print("there are %d Support Vectors" % shape(sVs)[0])
m,n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print("the training error rate is: %f" % (float(errorCount)/m))
dataArr,labelArr = loadDataSet('testSetRBF2.txt')
errorCount = 0
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
m,n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print("the test error rate is: %f" % (float(errorCount)/m)) testRbf()L==H
fullSet, iter: 0 i:0, pairs changed 0
...
there are 26 Support Vectors
the training error rate is: 0.090000
the test error rate is: 0.180000