【机器学习】贝叶斯参数估计法
一、贝叶斯参数估计
-
前导篇:【机器学习】最大似然估计与最大后验估计
-
这里先回顾一下最大后验估计法:
- 最大后验估计法,通过最大化参数 θ θ θ的后验分布来求出估计参数 θ ^ \hat{θ} θ^ : θ ^ = a r g max θ P ( θ ∣ x ) = a r g max θ P ( x ∣ θ ) ∗ P ( θ ) \hat{θ}=arg\max_θP(θ|x)=arg\max_θP(x|θ)*P(θ) θ^=argθmaxP(θ∣x)=argθmaxP(x∣θ)∗P(θ)
- 现在我们分析分析后验分布 P ( θ ∣ x ) P(θ|x) P(θ∣x): P ( θ ∣ x ) = P ( x ∣ θ ) ∗ P ( θ ) P ( x ) P(θ|x)=\frac{P(x|θ)*P(θ)}{P(x)} P(θ∣x)=P(x)P(x∣θ)∗P(θ) P ( x ) P(x) P(x)为常数,对优化问题不影响,所以可以记作: P ( θ ∣ x ) = P ( x ∣ θ ) ∗ P ( θ ) P(θ|x)=P(x|θ)*P(θ) P(θ∣x)=P(x∣θ)∗P(θ)
- P ( x ∣ θ ) P(x|θ) P(x∣θ)为样本的概率分布, P ( θ ) P(θ) P(θ)为参数 θ θ θ的先验分布。我们将样本 x x x带入后: P ( θ ∣ x ) P(θ|x) P(θ∣x)就是一个 θ θ θ的概率分布,即 θ θ θ后验分布。既然它是一个概率分布,我们可以简单的把它理解为一个概率密度函数 f ( θ ) f(θ) f(θ),即 f ( θ ) = P ( θ ∣ x ) f(θ)=P(θ|x) f(θ)=P(θ∣x),最大后验估计法就是用该函数 ( f ( θ ) ) (f(θ)) (f(θ))的最大值点作为我们估计的参数: θ ^ \hat{θ} θ^
-
贝叶斯参数估计法是最大后验估计法的加强版:
- 先引入损失函数: L ( θ , a ) L(θ,a) L(θ,a),这个地方对于损失函数中变量的含义,很多博客和资料说法都不一致,这里只是根据个人理解给出中间两个变量的含义:
- θ θ θ:是后验分布的随机变量, θ θ θ的分布函数为: f ( θ ) = P ( θ ∣ x ) f(θ)=P(θ|x) f(θ)=P(θ∣x)
- a a a:也是一个随机变量,也可以理解为一个普通自变量,最后用 a a a来估计贝叶斯参数估计法得出的 θ ^ \hat{θ} θ^。
- 参数的后分布 P ( θ ∣ x ) P(θ|x) P(θ∣x)还有一个含义:原本参数 θ θ θ是服从先验分布 P ( θ ) P(θ) P(θ)的,当我们获得样本数据 x x x后,将样本数据的以下统计信息加入到 θ θ θ分布中后, θ θ θ变成服从后验验分布 P ( θ ∣ x ) P(θ|x) P(θ∣x)的随机变量了。
- 现在假设我们有了样本数据 X X X,和损失函数 L ( θ , a ) L(θ,a) L(θ,a)。
- 首先我们将样本信息加入到 θ θ θ分布中,得到 θ θ θ当前服从的后验分布 P ( θ │ x ) P(θ│x) P(θ│x)。
- 得到了参数 θ θ θ当前的概率分布 P ( θ │ x ) P(θ│x) P(θ│x)后,我们就可以计算损失函数 L ( θ , a ) L(θ,a) L(θ,a)相对参数 θ θ θ的数学期望了: E θ ( L ( θ , a ) ) = ∫ L ( θ , a ) P ( θ │ x ) d θ E_θ (L(θ,a))=∫L(θ,a)P(θ│x)dθ Eθ(L(θ,a))=∫L(θ,a)P(θ│x)dθ这是一个a的函数叫做:贝叶斯风险
- 最后贝叶斯参数估计法通过最小化贝叶斯风险得到最后的参数估计值 θ ^ \hat{θ} θ^,即: θ ^ = a r g min a E θ ( L ( θ , a ) ) \hat{θ}=arg\min_aE_θ (L(θ,a)) θ^=argaminEθ(L(θ,a))
- 先引入损失函数: L ( θ , a ) L(θ,a) L(θ,a),这个地方对于损失函数中变量的含义,很多博客和资料说法都不一致,这里只是根据个人理解给出中间两个变量的含义:
-
贝叶斯参数估计法步骤:
- 第一步:计算后验分布 P ( θ │ x ) P(θ│x) P(θ│x): P ( θ │ x ) = P ( x │ θ ) ∗ P ( θ ) P ( x ) P(θ│x)=\frac{P(x│θ)*P(θ)}{P(x)} P(θ│x)=P(x)P(x│θ)∗P(θ)
- 第二步:计算贝叶斯风险: E θ ( L ( θ , a ) ) = ∫ L ( θ , a ) P ( θ ∣ x ) d θ E_θ (L(θ,a))=∫L(θ,a) P(θ|x)dθ Eθ(L(θ,a))=∫L(θ,a)P(θ∣x)dθ
- 第三步:最小化贝叶斯风险得到 θ ^ \hat{θ} θ^: θ ^ = a r g min a E θ ( L ( θ , a ) ) \hat{θ}=arg \min_aE_θ (L(θ,a)) θ^=argaminEθ(L(θ,a))
-
由上面的推导过程我们知道,贝叶斯参数估计法求解过程有两个难点:
- 第一个:求后验分布
- 第二步:最小化贝叶斯风险,涉及积分以及最小值求解
二、共轭分布
- 共轭先验:设资料 X X X有概率密度函数 F : X ∼ F ( x ∣ θ ) F:X∼F(x|θ) F:X∼F(x∣θ). θ θ θ的先验分布 π ( θ ) π(θ) π(θ)属于某个分布族 P : π ( θ ) ∈ P . P:π(θ)∈P. P:π(θ)∈P. 如果 θ θ θ的后验分布: π ( θ ∣ x ) π(θ|x) π(θ∣x)也属于分布族 P P P,那么 P P P就叫做 F F F的共轭先验。
- 假设样本 x x x的分布为: f ( x ∣ θ ) f(x|θ) f(x∣θ), θ θ θ的先验分布 π ( θ ) π(θ) π(θ)分布已知。如果 π ( θ ) π(θ) π(θ)与 f ( x ∣ θ ) f(x|θ) f(x∣θ)共轭,那么 π ( θ ) π(θ) π(θ)与 π ( θ ∣ x ) π(θ|x) π(θ∣x)会有一样的形式,这样不就会很方便求解后验分布 π ( θ ∣ x ) π(θ|x) π(θ∣x)了吗?这样将先验分布设计成与 f ( x ∣ θ ) f(x|θ) f(x∣θ)共轭,后面计算会很方便。
- 幸运的是我们可以证明,所有属于指数族分布的 f ( x ∣ θ ) f(x|θ) f(x∣θ),都可以求出它的共轭先验分布 π ( θ ) π(θ) π(θ)的具体形式。而大部分常见的分布都属于指数族分布,比如正态分布,指数分布,二项分布,泊松分布,Beta分布,Gamma分布等等。
- 常用的共轭分布:: 其中整体分布,就是样本分布 f ( x ∣ θ ) f(x|θ) f(x∣θ)。如果你的样本的分布是上面表中第一列中的一项,那么就可以将先验分布设计成第三列中对应的分布。所以在才会在那么多算法或实际问题中将某个参数的先验分布定义成Gamma或Beta这种“奇怪”的形式,原因就是为了求解方便。这就解决了第一个难题:求后验分布
Gamma 分布:
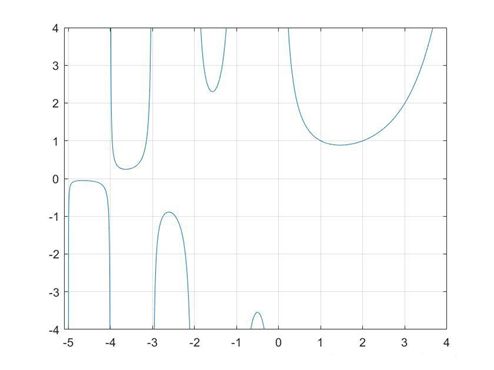
- Gamma函数: Γ ( x ) = ∫ 0 ∞ t x − 1 e − t d t Γ(x)=∫_0^∞t^{x-1} e^{-t} dt Γ(x)=∫0∞tx−1e−tdt
- Gamma函数图像:
- 通过分部积分法,可以很容易证明Gamma函数具有如下之递归性质: Γ ( x + 1 ) = x Γ ( x ) Γ(x+1)=xΓ(x) Γ(x+1)=xΓ(x) Γ ( x ) = ( x − 1 ) ! Γ(x)=(x-1)! Γ(x)=(x−1)!
- Gamma分布:
- 根据 Γ Γ Γ函数的定义有: ∫ 0 ∞ x α − 1 e − x Γ ( α ) d x = 1 ∫_0^∞\frac{x^{α-1} e^{-x}}{Γ(α)} dx=1 ∫0∞Γ(α)xα−1e−xdx=1
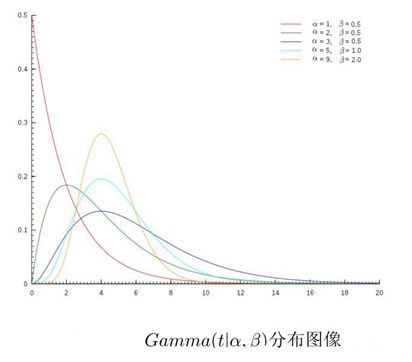
- 取积分中的函数作为概率密度,就得到了一个形式最简单的Gamma分布,其概率密度函数为: G a m m a ( x ∣ α ) = x α − 1 e − x Γ ( α ) Gamma(x|α)=\frac{x^{α-1} e^{-x}}{Γ(α)} Gamma(x∣α)=Γ(α)xα−1e−x其中, α α α为Gamma分布的shape parameter,主要决定了曲线的形状;而 β β β为Gamma分布的 rate parameter,主要决定了曲线有多陡。Gamma分布的归一化常数恰为 Γ Γ Γ函数在点 α α α处的值 Γ ( α ) Γ(α) Γ(α)。
- Gamma分布的期望、方差: E ( t ) = α β E(t)=\frac{α}{β} E(t)=βα D ( t ) = α β 2 D(t)=\frac{α}{β^2} D(t)=β2α
- Gamma分布的图像:
Beta分布:
- Beta函数: B ( α , β ) = ∫ 0 1 x α − 1 ( 1 − x ) β − 1 d x B(α,β)=∫_0^1x^{α-1} (1-x)^{β-1} dx B(α,β)=∫01xα−1(1−x)β−1dx其中 α , β > 0 α,β>0 α,β>0
- Beta函数性质:
- 对称性: B ( α , β ) = B ( β , α ) B(α,β)=B(β,α) B(α,β)=B(β,α)
- 与 Γ Γ Γ函数的关系: B ( α , β ) = Γ ( α ) Γ ( β ) Γ ( α + β ) B(α,β)=\frac{Γ(α)Γ(β)}{Γ(α+β)} B(α,β)=Γ(α+β)Γ(α)Γ(β)
- 根据Beta函数的定义有: ∫ 0 1 p α − 1 ( 1 − p ) β − 1 B ( α , β ) d p = 1 ∫_0^1\frac{p^{α-1} (1-p)^{β-1}}{B(α,β)} dp=1 ∫01B(α,β)pα−1(1−p)β−1dp=1
- 上式中取积分中的函数作为概率密度,就得到了Beta分布: B ( p ∣ α , β ) = p α − 1 ( 1 − p ) β − 1 B ( α , β ) B(p|α,β)=\frac{p^{α-1} (1-p)^{β-1}}{B(α,β)} B(p∣α,β)=B(α,β)pα−1(1−p)β−1
- 可以发现Beta分布的归一化常数恰为Beta函数在 ( α , β ) (α,β) (α,β)处的值.
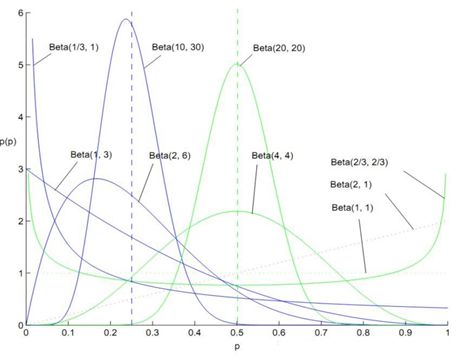
- Beta 分布的期望、方差: E ( p ) = α β + α E(p)=\frac{α}{β+α} E(p)=β+αα D ( p ) = β α ( β + α ) 2 ( β + α + 1 ) D(p)=\frac{βα}{(β+α)^2 (β+α+1)} D(p)=(β+α)2(β+α+1)βα
- Beta 分布的图像:
三、损失函数
- 贝叶斯估计的最后一步需要求下面式子: θ ^ = a r g min a E θ ( L ( θ , a ) ) \hat{θ}=arg\min_aE_θ (L(θ,a)) θ^=argaminEθ(L(θ,a))其中涉及积分以及最小值求解,看起来十分麻烦。所幸的是在特定的损失函数形式下,上面最后一步可以化简,并不需要完全用到积分。下面一部分的讲解就是在三种特定损失函数形式下贝叶斯估计的计算方法。
- 平方损失函数:
- 公式: L ( θ , a ) = ( θ − a ) 2 L(θ,a)=(θ-a)^2 L(θ,a)=(θ−a)2
- 若损失函数是平方损失函数,那么 θ ^ \hat{θ} θ^等于后验概率 π ( θ ∣ x ) π(θ|x) π(θ∣x)期望值,即当 a a a等于 θ θ θ在 π ( θ ∣ x ) π(θ|x) π(θ∣x)上的期望时,贝叶斯风险最小。
- 绝对值损失函数:
- 公式: L ( θ , a ) = ∣ θ − a ∣ L(θ,a)=|θ-a| L(θ,a)=∣θ−a∣
- 若损失函数是绝对值损失函数,那么 θ ^ \hat{θ} θ^等于 X X X的中位数,那么当 a a a等于数据 X X X的中位数时,贝叶斯风险最小
- 0-1损失函数:
- 公式: L ( θ , a ) = { 0 , ∣ θ − a ∣ ≤ Δ 1 , ∣ θ − a ∣ > Δ L(θ,a)=\begin{cases}0, &|θ-a|≤Δ \\1 ,& |θ-a|>Δ\end{cases} L(θ,a)={0,1,∣θ−a∣≤Δ∣θ−a∣>Δ
- 若损失函数是0-1损失函数且 Δ Δ Δ很小,当 a = a r g m a x π ( θ ∣ x ) a=argmax π(θ|x) a=argmaxπ(θ∣x)时,即 a a a等于 θ θ θ后验分布的最大值时,贝叶斯风险最小。
四、例子
- 假设: X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn是独立同分布的,且都服从泊松分布, X i ∼ P o i ( λ ) X_i∼Poi(λ) Xi∼Poi(λ). λ λ λ是要估计的参数。使用均方误差作为损失函数。
- 第一步:利用 λ λ λ的共轭先验求 λ λ λ的后验分布:
- 由 X i ∼ P o i ( λ ) X_i∼Poi(λ) Xi∼Poi(λ)可知样本分布为: f ( x │ λ ) = e − λ λ x x ! f(x│λ)=\frac{e^{-λ} λ^x}{x!} f(x│λ)=x!e−λλx
- 因为 X i X_i Xi是独立同分布,所以它的联合概率密度函数是: f ( X │ λ ) = e − n λ λ ∑ i = 1 n x i ∐ i = 1 n x ! f(X│λ)=\frac{e^{-nλ} λ^{∑_{i=1}^nx_i }}{∐_{i=1}^nx!} f(X│λ)=∐i=1nx!e−nλλ∑i=1nxi
- 泊松分布的共轭先验分布是Gamma分布,所以假设参数 λ λ λ的先验分布为: π ( λ ) = β α λ α − 1 e − β t Γ ( α ) π(λ)=\frac{β^α λ^{α-1} e^{-βt}}{Γ(α)} π(λ)=Γ(α)βαλα−1e−βt α , β α,β α,β是已知参数。
- 求解 X X X的边缘概率密度函数 f ( x ) f(x) f(x): f ( x ) = ∫ 0 ∞ e − n λ λ ∑ i = 1 n x i ∐ i = 1 n x ! π ( λ ) d λ = ∫ 0 ∞ e − n λ λ ∑ i = 1 n x i ∐ i = 1 n x ! β α λ α − 1 e − β t Γ ( α ) d λ f(x)=∫_0^∞\frac{e^{-nλ} λ^{∑_{i=1}^nx_i }}{∐_{i=1}^nx!} π(λ)dλ=∫_0^∞\frac{e^{-nλ} λ^{∑_{i=1}^n x_i }}{∐_{i=1}^nx!} \frac{β^α λ^{α-1} e^{-βt}}{Γ(α)} dλ f(x)=∫0∞∐i=1nx!e−nλλ∑i=1nxiπ(λ)dλ=∫0∞∐i=1nx!e−nλλ∑i=1nxiΓ(α)βαλα−1e−βtdλ = ( 1 n + β ) ∑ i = 1 n x i + α β α Γ ( α ) ∐ i = 1 n ( x ! ) ∫ 0 ∞ ( ( n + β ) λ ) ∑ i = 1 n x i + α − 1 e ( n + β ) λ d ( n + β ) λ =(\frac{1}{n+β})^{∑_{i=1}^n x_i +α} \frac{β^α}{Γ(α) ∐_{i=1}^n(x!) } ∫_0^∞ \frac{((n+β)λ)^{∑_{i=1}^n x_i +α-1}}{e^{(n+β)λ} } d(n+β)λ =(n+β1)∑i=1nxi+αΓ(α)∐i=1n(x!)βα∫0∞e(n+β)λ((n+β)λ)∑i=1nxi+α−1d(n+β)λ = ( 1 n + β ) ∑ i = 1 n x i + α β α Γ ( α ) ∐ i = 1 n ( x ! ) Γ ( ∑ i = 1 n x i + α ) =(\frac{1}{n+β})^{∑_{i=1}^n x_i +α} \frac{β^α}{Γ(α) ∐_{i=1}^n(x!) } Γ(∑_{i=1}^n x_i +α) =(n+β1)∑i=1nxi+αΓ(α)∐i=1n(x!)βαΓ(i=1∑nxi+α)
- 根据贝叶斯定理求解 λ λ λ的后验分布: π ( λ ∣ x ) = f ( x ∣ λ ) π ( λ ) f ( x ) π(λ|x)=\frac{f(x|λ)π(λ)}{f(x)} π(λ∣x)=f(x)f(x∣λ)π(λ) = e − n λ λ ∑ i = 1 n x i ∐ i = 1 n x ! β α λ α − 1 e − β t Γ ( α ) Γ ( α ) ∐ i = 1 n ( x ! ) ( n + β ) ∑ i = 1 n x i + α β α Γ ( ∑ i = 1 n x i + α ) =\frac{e^{-nλ} λ^{∑_{i=1}^nx_i }}{∐_{i=1}^nx!} \frac{β^α λ^{α-1} e^{-βt}}{Γ(α)} \frac{Γ(α) ∐_{i=1}^n(x!) (n+β)^{∑_{i=1}^nx_i +α}}{β^α Γ(∑_{i=1}^nx_i +α) } =∐i=1nx!e−nλλ∑i=1nxiΓ(α)βαλα−1e−βtβαΓ(∑i=1nxi+α)Γ(α)∐i=1n(x!)(n+β)∑i=1nxi+α = e − ( n + β ) λ λ ∑ i = 1 n x i + α − 1 ( n + β ) ∑ i = 1 n x i + α Γ ( ∑ i = 1 n x i + α =\frac{e^{-(n+β)λ} λ^{∑_{i=1}^n x_i +α-1} (n+β)^{∑_{i=1}^n x_i +α}}{Γ(∑_{i=1}^n x_i +α} =Γ(∑i=1nxi+αe−(n+β)λλ∑i=1nxi+α−1(n+β)∑i=1nxi+α
- 上面的式子很复杂,但其实它是一个Gamma分布: π ( λ ∣ x ) ∼ Γ ( ∑ i = 1 n x i + α , n + β ) π(λ|x)∼Γ(∑_{i=1}^nx_i+α,n+β) π(λ∣x)∼Γ(i=1∑nxi+α,n+β)
- 上面的求解过程还是太复杂,其实有更简便的方法。因为共轭先验分布是Gamma分布,所以后验分布肯定也是Gamma,我们可以直接凑出后验分布的形式,但不是很直观.
- 第二步:求在均方误差下 λ λ λ的贝叶斯估计 λ ^ b a y e s \hat{λ}_{bayes} λ^bayes
- 均方误差下的贝叶斯估计就是后验分布的期望,所以有: λ ^ b a y e s = ∑ i = 1 n x i + α n + β \hat{λ}_{bayes}=\frac{∑_{i=1}^nx_i+α}{n+β} λ^bayes=n+β∑i=1nxi+α
- 总结: 可以看到先验分布中λ服从参数为 α α α和 β β β的Gamma分布,在观察到一些数据后, λ λ λ仍然是服从Gamma分布的,只不过参数得到了修正,变成了 ∑ i = 1 n x i + α 和 n + β ∑_{i=1}^nx_i+α和n+β ∑i=1nxi+α和n+β. 这就是贝叶斯估计的思想,先假设参数服从某个分布,可能会有偏差。有偏差不要紧,我们将观察到的数据(样本)带入贝叶斯估计的过程便可以修正这些偏差
参考链接
- https://blog.csdn.net/jinping_shi/article/details/53444100
- https://blog.csdn.net/zengxiantao1994/article/details/72889732