最短路之dijsktra算法
Dijksatr算法是典型最短路算法,用于计算一个节点到其他所有节点的最短路径,主要特点是以起始点为中心向外层层扩展,直到拓展到终点为止。
那么dijkstra算法有什么特点呢?
(1):单源最短路径算法,时间复杂度:O(n^2)
(2)有向无向图都可以
(3)边的权值不能为负数
设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
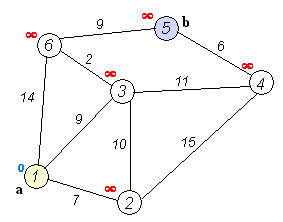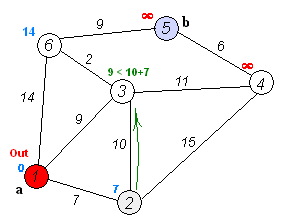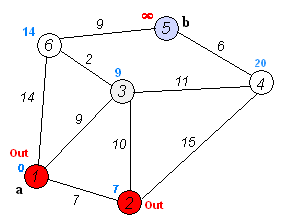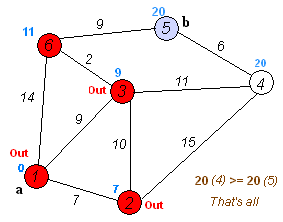
原理图:
3.迪杰斯特拉算法的实现过程
①先取一点v[0]作为起始点,初始化dis[i],d[i]的值为v[0]到其余点v[i]的距离w[0][i],如果直接相邻初始化为权值,否则初始化为无限大;
②将v[0]标记,vis[0] = 1(vis一开始初始化为0);
③找寻与v[0]相邻的最近点v[k],将v[k]点记录下来,v[k]与v[0]的距离记为min;
④把v[k]标记,vis[k]=1;
⑤查询并比较,让dis[j]与min+w[k][j]进行比较,判断是直接v[0]连接v[j]短,还是经过v[k]连接v[j]更短,即dis[j]=MIN(dis[j],min+w[k][j]);
⑥继续重复步骤③与步骤⑤,知道找出所有点为止。
dijkstra 题目
#include
#include
#include
#define inf 0x3f3f3f3f
using namespace std;
int maze[1010][1010],d[1010],n;
void dijkstra()
{
int vis[1010]={0},x;
for(int i=1;i<=n;i++)
d[i]=maze[i][1];
vis[1]=1;
for(int i=1;i
Dijkstra 单源最短路 邻接矩阵形式 双路径信息
/*
* 单源最短路径,dijkstra算法,邻接矩阵形式,复杂度为O(n^2)
* 两点间距离存入map[][],两点间花费存入cost[][]
* 求出源st到所有点的最短路径及其对应最小花费
* 返回各点的最短路径lowdis[]以及对应的最小花费lowval[]
* 可更改路径权类型,但是权值必须为非负,下标1~n
*/
const int MAXN = 1010;
const int INF = 0x3f3f3f3f;
int n, m;
int lowdis[MAXN];
int lowval[MAXN];
int visit[MAXN];
int map[MAXN][MAXN];
int cost[MAXN][MAXN];
void dijkstra(int st)
{
int temp = 0;
for (int i = 1; i <= n; i++)
{
lowdis[i] = map[st][i];
lowval[i] = cost[st][i];
}
memset(visit, 0, sizeof(visit));
visit[st] = 1;
for (int i = 1; i < n; i++)
{
int MIN = INF;
for (int j = 1; j <= n; j++)
{
if (!visit[j] && lowdis[j] < MIN)
{
temp = j;
MIN = lowdis[j];
}
}
visit[temp] = 1;
for (int j = 1; j <= n; j++)
{
if (!visit[j] && map[temp][j] < INF)
{
if (lowdis[j] > lowdis[temp] + map[temp][j])
{
lowdis[j] = lowdis[temp] + map[temp][j];
lowval[j] = lowval[temp] + cost[temp][j];
}
else if (lowdis[j] == lowdis[temp] + map[temp][j])
{
if (lowval[j] > lowval[temp] + cost[temp][j])
{
lowval[j] = lowval[temp] + cost[temp][j];
}
}
}
}
}
return ;
}
Dijkstra 起点Start 结点有权值
st int inf = 0x3f3f3f3f;
int num[M]; // 结点权值
int map[M][M]; // 图的临近矩阵
int vis[M]; // 结点是否处理过
int ans[M]; // 最短路径结点权值和
int dis[M]; // 各点最短路径花费
int n, m, Start, End; // n结点数,m边数,Start起点,End终点
void Dij(int v)
{
ans[v] = num[v];
memset(vis, 0, sizeof(vis));
for (int i = 0; i < n; ++i)
{
if (map[v][i] < inf)
{
ans[i] = ans[v] + num[i];
}
dis[i] = map[v][i];
}
dis[v] = 0;
vis[v] = 1;
for (int i = 1; i < n; ++i)
{
int u = 0, min = inf;
for (int j = 0; j < n; ++j)
{
if (!vis[j] && dis[j] < min)
{
min = dis[j];
u = j;
}
}
vis[u] = 1;
for (int k = 0; k < n; ++k)
{
if (!vis[k] && dis[k] > map[u][k] + dis[u])
{
dis[k] = map[u][k] + dis[u];
ans[k] = ans[u] + num[k];
}
}
for (int k = 0; k < n; ++k)
{
if (dis[k] == map[u][k] + dis[u])
{
ans[k] = max(ans[k], ans[u] + num[k]);
}
}
}
printf("%d %d\n", dis[End], ans[End]); // 输出终点最短路径花费、最短路径结点权值和
}
int main()
{
scanf("%d%d%d%d", &n, &m, &Start, &End);
for (int i = 0; i < n; ++i)
{
scanf("%d", &num[i]);
}
memset(vis, 0, sizeof(vis));
memset(map, 0x3f, sizeof(map));
for (int i = 0; i < m; ++i)
{
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
if (map[x][y] > z)
{
map[x][y] = z;
map[y][x] = z;
}
}
Dij(Start);
return 0;