Python蒙特卡洛算法

一、什么是蒙特卡洛算法？

蒙特卡洛（Monte Carlo）法是一类随机算法的统称。随着二十世纪电子计算机的出现，蒙特卡洛法已经在诸多领域展现出了超强的能力。在机器学习和自然语言处理技术中，常常被用到的MCMC也是由此发展而来。

二、应用

1、求圆周率 π

一个正方形内部相切一个圆，圆的面积是 $C$，正方形的面积 $S$，圆和正方形的面积之比是 $\frac{\pi }{4}$。
$$\frac{C}{S}=\frac{\pi r^2}{4r^2}=\frac{\pi }{4}$$

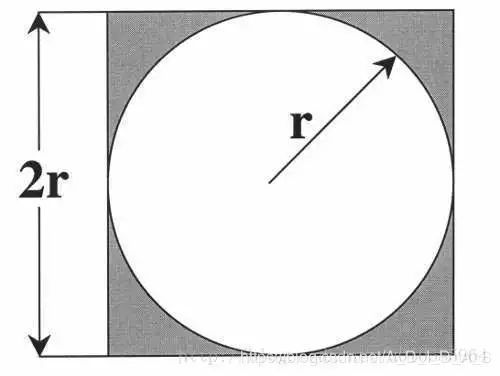
在这个正方形内部，随机产生n个点（这些点服从均匀分布），计算它们与中心点的距离是否大于圆的半径，以此判断是否落在圆的内部。落在圆内部的点数统计出来是m个点。那么m、n点数个数的比例也符合面积的比：
$$\frac{m}{n}=\frac{\pi }{4}$$
m与n的比值乘以4，就是π的值:
$$\pi =\frac{4m}{n}$$
如果m、n足够大的话，那么就可以较为精确的求出π的值。

2、求定积分（投点法）

求解 $\pi$ 的方法也可以用来求解定积分，通常被称为投点法。如下图所示，有一个函数$f(x)$，若要求它从 $a$ 到 $b$ 的定积分，其实就是求曲线下方的面积。这时我们可以用一个比较容易算得面积的矩型罩在函数的积分区间上（假设其面积为 $Area$）。然后随机地向这个矩形框里面投点，其中落在函数 $f(x)$ 下方的点为绿色，其它点为红色。然后统计绿色点的数量占所有点（红色+绿色）数量的比例为 $r$，那么就可以据此估算出函数 $f(x)$ 从 $a$ 到 $b$ 的定积分为 $Area\times r$ 。

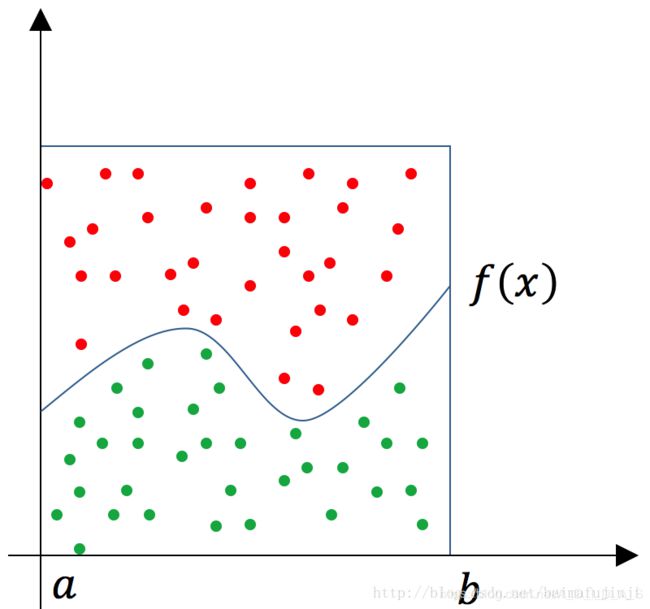
注意由蒙特卡洛法得出的值并不是一个精确之，而是一个近似值。而且当投点的数量越来越大时，这个近似值也越接近真实值。

3、求定积分（期望法）

下面我们来重点介绍一下利用蒙特卡洛法求定积分的第二种方法——期望法，有时也成为平均值法。
任取一组相互独立、同分布的随机变量$\{X_i\}$，$X_i$ 在$[a,b]$上服从分布律 $f_X$，也就是说 $f_X$是随机变量 $X$的PDF（概率密度函数），令 $g^{\ast }(x)=\frac{g(x)}{f_X(x)}$，则 $g^{\ast }(x)$ 也是一组独立同分布的随机变量，而且（因为 $g^{\ast }(x)$ 是关于 $x$ 的函数，所以根据LOTUS可得）
$$E[g^{\ast }(X_i)]={\int }_a^b{g}^{\ast }(x)f_X(x)dx={\int }_a^{b}g(x)dx=I$$
由强大数定理可得：
$$P_r(\underset{N->\infty }{\lim }\frac{1}{N}\sum _{i=1}^N{g}^{\ast }(X_i)=I)=1$$
若选
$$\overline{I}=\frac{1}{N}\sum _{i=1}^N{g}^{\ast }(X_i)$$
则 $\overline{I}$ 依概率1收敛到 $I$，平均值法就用 $\overline{I}$ 作为 $I$ 的近似值。
假设要计算的积分有如下形式
$$I={\int }_a^{b}g(x)dx$$
其中被积函数 $g(x)$ 在区间 $[a,b]$ 内可积。任意选择一个有简便办法可以进行抽样的概率密度函数$f_X(x)$，使其满足下列条件：

1. 当 $g(x)≠0$，$f_X(x)≠0（a\le x\le b）$
2. ${\int }_a^b{f}_X(x)dx=1$

如果记
$$g^{\ast }(x)=\{\begin{array}{ll}\frac{g(x)}{f_X(x)}& f_X(x)≠0\\ 0& f_X(x)=0\end{array}$$
那么原积分式可以写作
$$I={\int }_a^b{g}^{\ast }(x)f_X(x)dx$$
因而求积分的步骤是：
1、产生服从分布律 $f_X$ 的随机变量 $X_i（i=1,2,3,...,N）$
2、计算均值
$$\overline{I}=\frac{1}{N}\sum _{i=1}^N{g}^{\ast }(X_i)$$
并用它作为 $I$ 的近似值。
如果 $a,b$ 为有限值，那么 $f_X$ 可取作为均匀分布：
$$f_X(x)=\{\begin{array}{ll}\frac{1}{b-a}& a\le x\le b\\ 0& otherwise\end{array}$$
此时原来的积分式变为
$$I=(b-a){\int }_a^{b}g(x)\frac{1}{b-a}dx$$
具体步骤如下：
1、产生服从分布律 $f_X$ 的随机变量 $X_i（i=1,2,3,...,N）$
2、计算均值
$$\overline{I}=\frac{1}{N}\sum _{i=1}^N{g}^{\ast }(X_i)$$
并用它作为 $I$ 的近似值。

4、平均值法（图形解释）

注意积分的几何意义就是 $[a,b]$ 区间内曲线下方的面积。

当我们在 $[a,b]$ 之间随机取一点x时，它对应的函数值就是 $f(x)$，然后变可以用 $f(x)\times (b-a)$ 来粗略估计曲线下方的面积（也就是积分），当然这种估计（或近似）是非常粗略的。

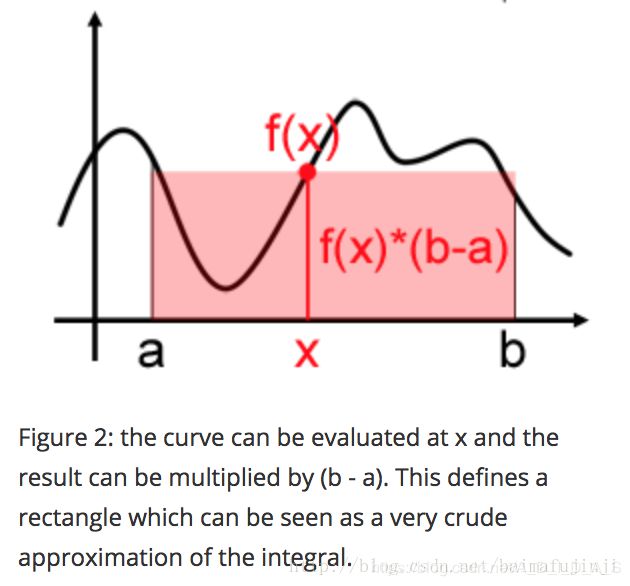
于是我们想到在 $[a,b]$ 之间随机取一系列点 $xi$ 时（$xi$ 满足均匀分布），然后把估算出来的面积取平均来作为积分估计的一个更好的近似值。可以想象，如果这样的采样点越来越多，那么对于这个积分的估计也就越来越接近。

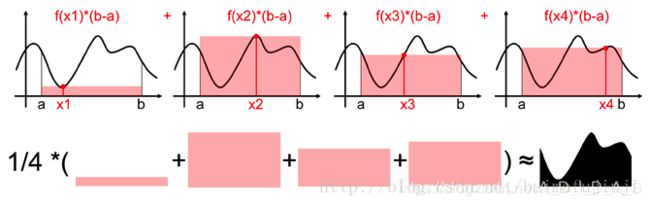
按照上面这个思路，我们得到积分公式为：
$$\overline{I}=(b-a)\frac{1}{N}\sum _{i=0}^{N-1}f(X_i)=\frac{1}{N}\sum _{i=0}^{N-1}\frac{f{X}_i}{\frac{1}{b-a}}$$
注意其中的 $\frac{1}{b-a}$ 就是均匀分布的PMF。这跟我们之前推导出来的蒙特卡洛积分公式是一致的。

三、代码

import random
import math
import numpy as np
from scipy import integrate

# 利用蒙特卡洛算法计算圆周率 PI
def calculate_PI(n):
    i = 0
    count = 0
    while i <= n:
        x = random.random()     # 生成 [0,1] 之间的随机浮点数
        y = random.random()
        if math.pow(x, 2) + math.pow(y, 2) < 1:
            count += 1

        i += 1

    PI = 4 * count / n
    print(f'PI 的值为 : {PI}')


''' 求积分 : y = x**2 在 [0,1] 内的积分 '''

# 利用蒙特卡洛算法计算定积分 (投点法)
def calculate_Integral1(n):
    count = 0
    x_min, x_max = 0.0, 1.0
    y_min, y_max = 0.0, 1.0

    for i in range(n):
        x = random.uniform(x_min, x_max)       # 随即生成一个在 [x_min, x_max] 之间的浮点数
        y = random.uniform(y_min, y_max)

        if y < x ** 2:
            count += 1

    integral_value = count / float(n)
    print(f'投点法求积分 : {integral_value}')


# 利用蒙特卡洛算法计算定积分 (期望法)
def calculate_Integral2(a,b,N):
    X = np.linspace(a, b, N)
    total = 0

    for x_i in X:
        total += x_i ** 2

    integral_value = (b - a) / N * total
    print(f'期望法求积分 : {integral_value}')


# 利用 scipy 库函数求积分
def use_scipy_library():
    val, err = integrate.quad(f, 0, 1)
    print(f'scipy 积分结果 : {val}')

def f(x):
    return x ** 2

if __name__ == '__main__':
    calculate_PI(10000)
    calculate_Integral1(10000)
    calculate_Integral2(0, 1, 100)
    use_scipy_library()

运行结果

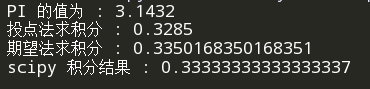
这里是对 $y=x^2$ 在 $[0,1]$ 上采用蒙特卡洛算法进行积分的结果，可以看到结果还是比较准确的，当我们选取的点数越多时，计算结果也就越准确。