【排序】直接插入排序

目录

直接插入排序原理

直接插入排序图文说明

代码实现

C实现

JAVA实现

 复杂度分析和稳定性

复杂度

稳定性

总结

直接插入排序原理

简单理解就是将待排序部分逐一向已排序的序列中插入，最直观的例子就是《算法导论》中的扑克牌的例子了，打扑克牌拿牌的过程就是一个直接插入的过程：手中的牌是已排序的序列，而剩余的牌都是无序的；并且在首次拿牌后，第一张牌在手中就默认为一个有序的序列，其后拿到的第二张牌与手中的牌相比较，选择放在前面后者后面，再往下的过程就是重复，第n张牌从后向依次与n-1、n-2、......张牌相比较，由于手中的牌是排好的升序序列，所以当拿到的排比被比较的牌小的时候，这个比较过程就不断向前的，直到第k张牌的位置，当第k张牌不再大于拿到牌的时候，就将这张牌插入到k+1的位置，这时候后面的牌的位置标号依次加一，总牌数增一。

直接插入排序图文说明

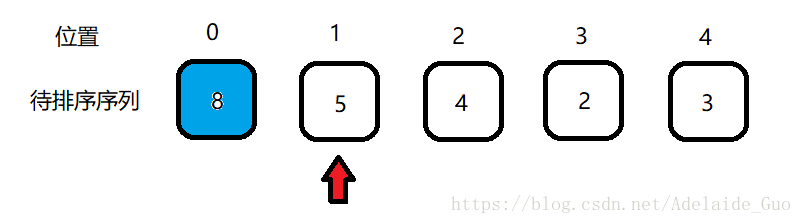
注：蓝色代表已排序序列，白色代表未排序序列，红色箭头指向未排序序列的第一个元素位置。

如图所示，现在有一个待排序序列[8 5 4 2 3]，首先默认初始状态下，位置0的数字8作为已排序序列，位置1--位置4的[5 4 2 3] 为待排序序列，之后就逐一从[5 4 2 3]中取出数字向前进行比较，插入到已排序序列的合适位置。

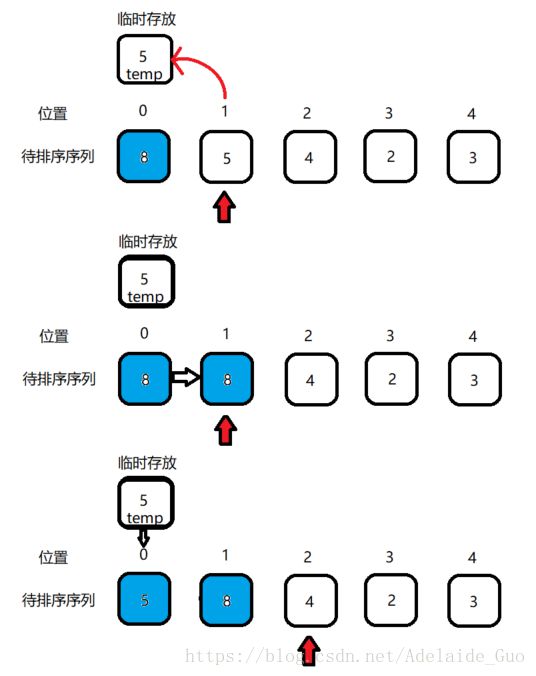
首先是[5 4 2 3]中位置1的数字5，与[8]位置0的数字8进行比较，很明显5<8，所以进行如下操作：

1. 将[5 4 2 3]中位置1的数字5，存放到临时变量temp；
2. 将[8]中[8]向后移一位（前一个[8]代表已派序列，后一个[8]是已排序列的子列，该子列中所有的元素都大于即将插入的数字，同样的，该子列也是一个已排序列。比如说已排序列是[1 2 4 5 6]，未排序是[3 7]，那么下一个动作就是将3插入到[1 2 4 5 6]中，依次比较后，[1 2 4 5 6]的子序列[4 5 6]需要向后移一位，未即将到来的数字3腾出一个位置。）；
3. 将临时变量数字5插入到位置0的位置，此时已排序列是[5 8]，未排序列[4 2 3]；

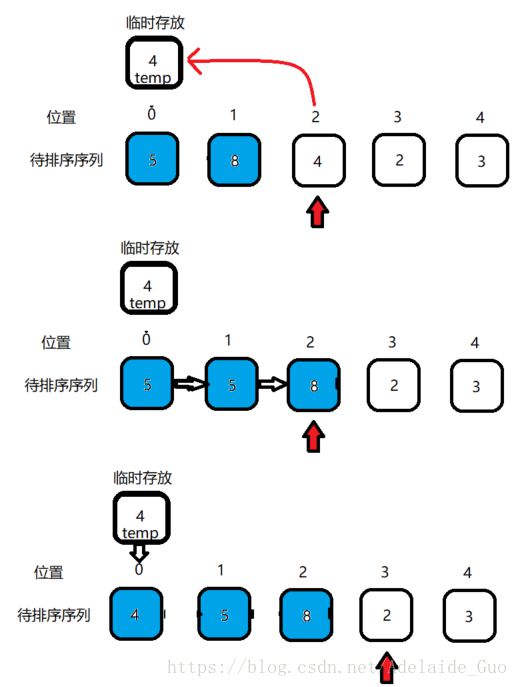
接下来拿出来[4 2 3]中的数字4，在已排序列[5 8]中从后向前进行比较：4<8，4<5。所以进行如下操作：

 详细过程和上面类似，已排序序列变为[4 5 8]，未排序序列[2 3]。之后的操作就依次重复，看图吧。

这里要说明一点，就是如果从待排序序列中拿出来要插入到已排序的元素比已排序中的最大元素还大，那就不需要进行移动操作，直接将已排序序列位置增加一位就可以了，比如序列[1 2 3 4 6 5]，初始状态是[1] [2 3 4 6 5]，前面是已排序，后面是未排序，但2>1,所以下一状态就是已排序：[1 2]，未排序 [3 4 6 5]；接下来依次[1 2 3] [4 6 5] ===> [1 2 3 4] [6 5] ===> [1 2 3 4 6] [5] ===>[1 2 3 4 5 6]结束，以上都是前为已排序序列，后为未排序序列。

代码实现

C实现

代码：

#include 

void insertSort(int a[], int n){
	int i, j;

	for(i = 1; i < n; i++){          //从待排序序列中取首个元素
		if(a[i] < a[i-1]){           //与已排序最大数值相比较，若大于则直接归入已排序，否则寻找合适位置
			int temp = a[i];         //将该元素存到临时变量中

			for(j = i-1; j>0 && a[j]>temp; j--){
				a[j+1] = a[j];       //寻找插入的合适位置，并将该位置后的所有元素向后移位，腾出地方给插入的元素
			}

			a[j+1] = temp;           //插入该元素
		}
	}
}

void main(){
	int i;
	int a[8] = { 8, 5, 4, 3, 2, 1, 6, 7 };

	printf("before:{");
	for(i = 0; i < 8; i++){
		printf("%d ",a[i]);
	}
	printf("}\n");

	insertSort(a,8);
	
	printf("after:{");
	for(i = 0; i < 8; i++){
		printf("%d ",a[i]);
	}
	printf("}\n");

}

测试结果：

JAVA实现

代码：

import java.util.Arrays;

/**
 * Created by GFC on 2018/8/28.
 */
public class StrightSort {

    public void sort(int[] array){
        int j;
        for (int i = 1; i < array.length; i++) {
            if(array[i-1] > array[i]){
                int temp = array[i];
                for (j = i-1; j >=0&& array[j]>temp ; j--) {
                    array[j+1] = array[j];
                }
                array[j+1] = temp;
            }
        }
    }

    public static void main(String[] args) {
        StrightSort sort = new StrightSort();
        int a[] = {8, 5, 4, 3, 2, 1, 6, 7};

        System.out.println("Before: " + Arrays.toString(a));
        sort.sort(a);
        System.out.println("After: " + Arrays.toString(a));
    }
}

测试结果：

 复杂度分析和稳定性

复杂度

最好情况就是待排序的序列是顺序序列，这样，只需要遍历次，就可以了，不存在移位的情况；最坏情况是待排序序列是完全逆序的，比如[n,n-1,n-2,......,2,1]这样情况下，初始状态时[n][n-1,n-2,......,2,1]（注：前半部分为已排序，后面为待排序也就是带插入元素的集合），接下来每一次都要将后面待排序的数字插入，都要将前面已排序序列向后整体移动一位，总共移动次数为1到n-1的和，即。所以时间复杂度为。

稳定性

由于判断条件是第i个元素是否小于第i-1个元素，也就是插入元素是否小于已排序中最后一位（最大元素），所以当想等情况下，直接将带插入元素改为第i+1个元素，第i个元素算入已排序序列当中，所以想等元素的相对位置不会发生变化，直接插入排序具有稳定性。

总结

直接插入排序比较容易理解，也是插入排序中最简单的方式，其他插入排序比如折半插入排序、希尔排序，也都是用了相同的思想去实现的。直接插入排序是稳定的，其时间复杂度为。