欧拉路径-欧拉回路

概念：
欧拉路径：经过图中所有的边一次（一笔画）是欧拉路径
欧拉回路：经过图中所有的边一次，并回到起点，是欧拉回路。
欧拉图：存在欧拉回路的图就是欧拉图
欧拉回路是欧拉路径，欧拉路径不一定是欧拉回路。
半欧拉图：只有欧拉路径（非回路）的图是半欧拉图。

判断一个无向图和有向图是否有欧拉路径和欧拉回路很简单，无向图看每个点的度数，有向图看每个点的出入度。

	欧拉路径	欧拉回路
无向图	奇度数结点数为 0 或 2	奇度数结点数为 0
有向图	起点的入度 - 出度 = -1，终点的入度 - 出度 = 1， 其余点入度=出度	每个结点的入度 = 出度

无向图中，如果奇度数点个数为2，可以直接看出该图是半欧拉图，有一个非回路的欧拉路径。而且以这两个点为起终点。

推荐一个不错的教程，来自油管的 WilliamFiset
Existence of Eulerian Paths and Circuits | Graph Theory

另一个有关欧拉路径回路的问题是找出欧拉路径回路。用深搜dfs就可以很容易的找出来了。
具体的说是 Hierholzer’s Algorithm —Hierholzer算法

具体思路有点像dfs版拓扑排序。这个算法前提是图已经是判断出来是有欧拉路径或欧拉图了，然后还要找到开始结点。无向图中，没有奇数点就随便找起点，有两个奇数点，这两个点就是起终点，可以随便选取一个做起点。有向图中，所有点出入度都相同就任意取起点，如果有一个入度-出度=-1的点，这个点就是起点，而且还有一个入度-出度=1的为终点。

起点找完，开始深搜，

1. 每搜一条边，要标记为走过，
2. 遇到阻塞（该结点没有后续邻边或该结点的邻边都搜完），该节点入栈，
3. 回溯，继续搜可以走的边，遇到阻塞一样要入栈。
4. 直到深搜结束，得到一个序列存在栈中
   因为每次都是阻塞了才入栈，说明每次入栈的点都是最靠后的，栈中的序列是倒序的。最后弹出元素得到的序列就是顺序的路径。

存图数据可以用邻接矩阵，也可以用邻接表，这里我用了邻接矩阵，写起来很方便，还可以用作标记数组，标记边的访问情况。

油管中的视频有动态的演示，推荐大家去看一看，逼站也有对应的翻译的视频
Eulerian Path Algorithm | Graph Theory

dfs求欧拉回路的方法大致如下：
伪代码：

fun dfs(u):
	for (v, v < n, v++):
		if (graph[u][v]):
			graph[u][v] = graph[v][u] = 0
			dfs(u)
	stack.put(u)

main:
	# graph[u][v] == 1 表示u-->v有边，0表示没边，如果有重边就可以在原来的基础上加1
	stack, graph[n][n] 
	if (has_euler_path()):
		start = find_start()
		dfs(start)
		while (!stack.empty)
			print(stack.pop())
	else:
		print("The graph do not exist Euler Path.")
	
	

由于dfs容易爆栈，这里用python写了个非递归的，用栈模拟递归的方法。从当前结点开始搜，搜到一个可以访问的结点就入栈，去边，break，继续上一层循环，直到遇到阻塞就出栈，把出栈的结点压入路径的栈中。

def get_path(st):
    """Hierholzer算法（非递归）"""
    path = []
    stack = [st]
    while stack:
        curnode = stack[-1]
        for v in range(n):
            if graph2[curnode][v]:
                graph2[curnode][v] -= 1  # 对应的边数减一
                graph2[v][curnode] -= 1
                stack.append(v)
                break
        else:
            path.append(stack.pop())
    return path

下面分别有无向图和有向图的欧拉路径的求解，大同小异，存储图的数据结构有所不同，判断是否有欧拉路径的方法不同，还有找起点一不同。

如果要求欧拉回路也是一样用dfs的方法。

完整 python 代码：(无向图)

""" 无向图欧拉路径的求解 """


def dfs(u):
    """Hierholzer算法（递归）"""
    for v in range(n):  # 遍历可以走的边
        if graph[u][v]:  # 判断这条边是否可以走
            graph[u][v] -= 1  # 对应的边数减一
            graph[v][u] -= 1
            dfs(v)
    # 遇到阻塞了（邻边都走完了），入栈
    stack.append(u)


def get_path(st):
    """Hierholzer算法（非递归）"""
    path = []
    stack = [st]
    while stack:
        curnode = stack[-1]
        for v in range(n):
            if graph2[curnode][v]:
                graph2[curnode][v] -= 1  # 对应的边数减一
                graph2[v][curnode] -= 1
                stack.append(v)
                break
        else:
            path.append(stack.pop())
    return path


def has_path():
    """判断图是否有欧拉路径"""
    global odc
    for i, dg in enumerate(degree):
        if dg % 2 == 1:
            odc += 1
            odd_degree_nodes.append(i)
    return odc == 0 or odc == 2


def find_start():
    """找起点"""
    if odc == 2:
        return sorted(odd_degree_nodes)[0]
    return 0


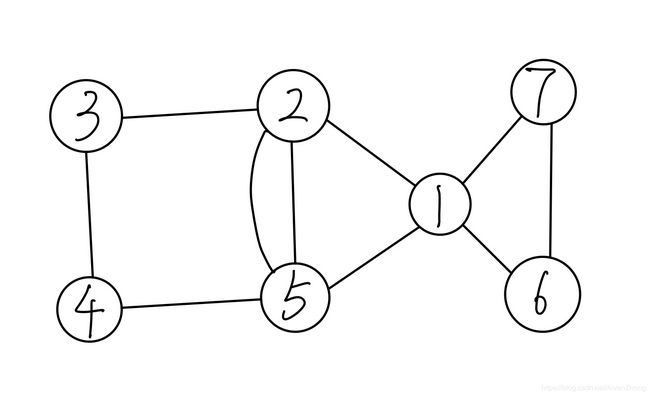
# 图数据（无向图）
edges = [
    [1, 2],
    [1, 5],
    [1, 6],
    [1, 7],
    [6, 7],
    [2, 5],
    [2, 5],
    [2, 3],
    [3, 4],
    [4, 5],
]

# 点，边个数
n, m = 7, 10

# 邻接矩阵，重边的对应的graph[u][v]和graph[v][u]自增一
graph = [[0] * n for _ in range(n)]

# 每个结点的度
degree = [0] * n

stack = []

odc = 0  # odd degree count
odd_degree_nodes = []

# 构建图
for u, v in edges:
    u, v = u - 1, v - 1
    graph[u][v] += 1
    graph[v][u] += 1
    degree[u] += 1
    degree[v] += 1

graph2 = [e[:] for e in graph]

# 欧拉路径
if has_path():
    print('The graph exist Euler Path')
    st = find_start()  # 递归
    dfs(st)
    path = get_path(st)  # 非递归
    [print(str(e) + " -> ", end='') for e in stack[::-1]]
    print()
    [print(str(e) + " -> ", end='') for e in path[::-1]]
else:
    print("The graph do not exist Euler Path.")

python 代码： （有向图）

""" 有向图欧拉路径的求解 """


def dfs(u):
    """Hierholzer算法"""
    for v in range(n):  # 遍历可以走的边
        if graph[u][v]:  # 判断这条边是否可以走
            graph[u][v] -= 1  # 对应的边数减一
            dfs(v)
    # 遇到阻塞了（邻边都走完了），入栈
    stack.append(u)


def has_path():
    """判断图是否有欧拉路径，顺便找到起点"""
    start_count, end_count = 0, 0
    global start
    for i in range(n):
        in_de, out_de = in_degree[i], out_degree[i]
        diff = in_de - out_de
        if diff == -1:
            start_count += 1
            start = i
        elif diff == 1:
            end_count += 1
        elif diff != 0:
            return False
    # 起终点都只有一个或者全部结点出入度差为0才有欧拉路径
    return start_count == 1 and end_count == 1 or start_count == 0 and out_degree == 0


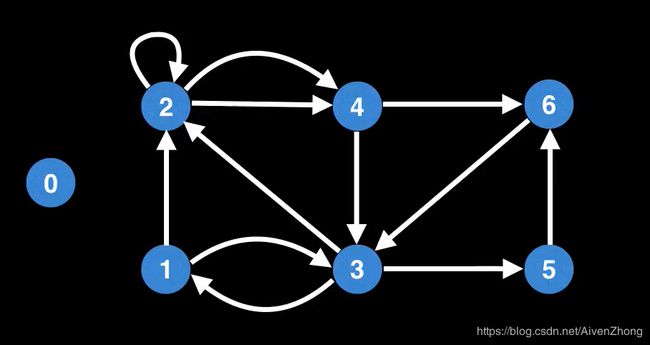
# 图数据（有向图）
edges = [
    [1, 2],
    [1, 3],
    [2, 2],
    [2, 4],
    [2, 4],
    [3, 1],
    [3, 2],
    [3, 5],
    [4, 3],
    [4, 6],
    [5, 6],
    [6, 3],
]

# 点，边个数
n, m = 7, len(edges)

# 邻接矩阵，重边的对应的graph[u][v]和graph[v][u]自增一
graph = [[0] * n for _ in range(n)]

# 每个结点的出入度
in_degree = [0] * n
out_degree = [0] * n

stack = []
start = 0

# 构建图
for u, v in edges:
    graph[u][v] += 1
    out_degree[u] += 1
    in_degree[v] += 1

# 欧拉路径
if has_path():
    print('The graph exist Euler Path')
    dfs(start)
    [print(str(e) + " -> ", end='') for e in stack[::-1]]
else:
    print("The graph do not exist Euler Path.")