平衡树——Treap (含完整模板)
平衡树——Treap
基本概念:
二叉搜索树(BST):
对于任意根节点,满足左儿子的权值<根节点的权值<右儿子的权值的二叉树。也就是说,BST的前序遍历的结果是从小到大的。通过BST,我们可以进行插入,删除元素等操作,还能记录一些信息查询更多东西。所有的操作都可以O(h)实现。h在最好的情况下是logn,但是在最坏情况下,BST可能会退化成链,复杂度极不稳定。那么能不能想办法使其平衡呢?于是就有了平衡树。
平衡二叉数:
有BST的性质,且通过一定的规则使二叉树尽量能保持平衡。所谓“平衡”就是左右子节点的深度保持接近(一般来说深度差小于2)。平衡树的种类多种多样,有Treap、伸展树,AVL、红黑树、替罪羊树等…
Treap的思想和实现细节:
总体思想:
Treap=tree+heap。除了原本键值key,Treap给每个节点添加了一个随机的优先级fix,对于key来说,Treap是BST。对于fix来说,Treap是一个堆。Treap就是通过fix的随机性在平均情况下保证平衡的。并通过旋转来维护Treap的性质。
Treap节点的定义:
struct node{
node* ch[2]; //左右儿子的指针
int key,fix,size,cnt; //各种信息
void maintain(){ size=ch[0]->size + ch[1]->size + cnt; }
};key:键值,fix:优先级,size:以这个节点为根的子树的节点个数(包括自己) ,cnt:相同元素重复次数(把key相同的元素放在一个节点)。Maintain()是在之后的操作中树改变后维护size的操作。
旋转:
Treap最核心的操作就是旋转(rotate)了:
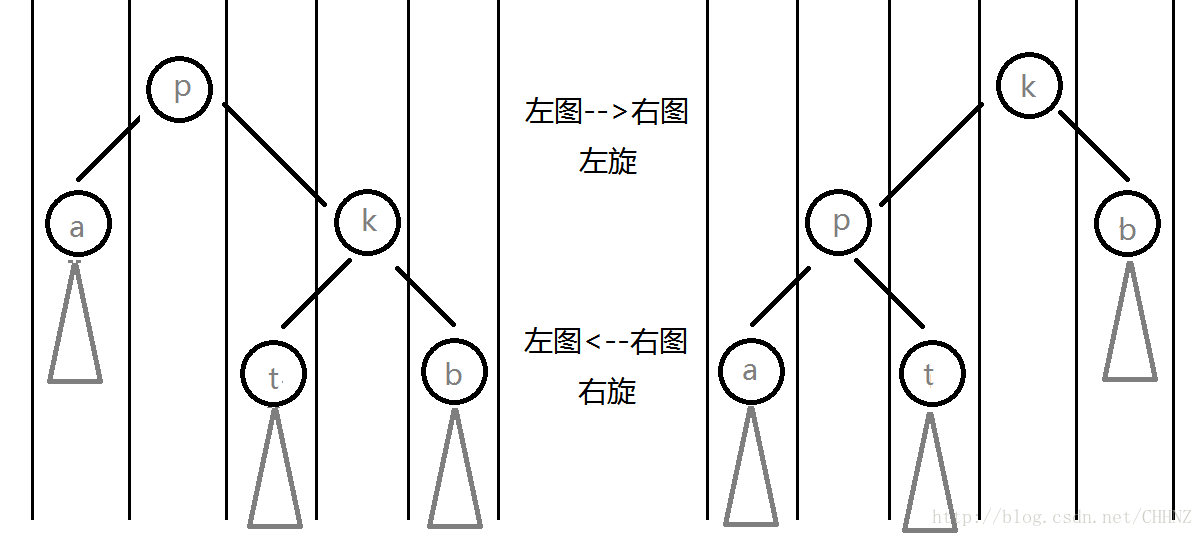
所谓左旋就是逆时针,右旋为顺时针。如图,旋转之后,节点的左右位置不变,即BST性质不变,而p与k的上下位置变化了,a和b的深度也发生变化了。通过旋转,我们也可以在不破坏BST性质的前提下维护堆性质。
void rot(P_node &p,int d){ //d为0表示左旋,d为1表示右旋。
P_node k=p->ch[d^1]; p->ch[d^1]=k->ch[d]; k->ch[d]=p;
p->maintain(); k->maintain(); p=k; //旋转完要修正,注意p是k的子节点,一定要先p再k
}光会旋转还不够,还要知道在什么时候旋转。具体运用看下面的插入删除操作。
插入元素(Insert):
如何插入新元素呢?先通过BST性质找到插入的位置,但是直接挂到最下层后不满足堆性质,所以通过不断旋转,使新节点慢慢往上爬,直到满足堆性质为止。结合堆的插入操作就很好理解了。通过递归实现特别简洁,代码如下:
void _Insert(P_node &p,int tkey){
if(p==null) p=newnode(tkey); else //新节点
if(p->key==tkey) p->cnt++; else{ //重复元素
int d=tkey>p->key;
_Insert(p->ch[d],tkey);
if(p->ch[d]->fix > p->fix) rot(p,d^1); //如果子节点优先级更大就把他转上来。
}
p->maintain(); //维护信息
}删除元素(Erase):
删除和插入道理一样,是逆向的过程。也就是说先通过旋转让要删除的元素往下走,走到最下层,他的有一个子节点为空,就用另一个儿子代替他,直接删除。
void _Erase(P_node &p,int tkey){
if(p->key==tkey){ //找到了目标
if(p->cnt>1) p->cnt--; else //重复元素
if(p->ch[0]==null) p=p->ch[1]; else
if(p->ch[1]==null) p=p->ch[0]; else{ //直接删除
int d=p->ch[0]->fix > p->ch[1]->fix; //往小的那边走,即把大的转上去作为根。
rot(p,d); _Erase(p->ch[d],tkey);
}
} else _Erase(p->ch[tkey>p->key],tkey); //继续向下找
p->maintain();
}上面是的插入删除基本操作,接下来是询问操作。
实现名次树:
求第k大的数(Kth)和求键值为tkey的值的排名(Rank):
这两个询问原理相似,只要搞清楚一个东西:对于当前以p为根的子树中,p->key的排名为:
[ p->ch[0]->size+1 , p->ch[0]->size+p->cnt ] (因为有相同元素,所以是一个区间)
这个很好理解,左子树的所有节点都比p大,所以得出这样的结果。处理询问时,只要根据当前根节点的key,判断是往左走还是往右走就行了。
int _Kth(P_node p,int k){
if(p==null||k<1||k>p->size) return 0; //询问出错,无答案
if(kch[0]->size+1) return _Kth(p->ch[0],k);
if(k>p->ch[0]->size+p->cnt) return _Kth(p->ch[1],k-p->ch[0]->size-p->cnt);
return p->key;
}
int _Rank(P_node p,int tkey,int res){ //res表示除了当前这颗子树,之前知道的比他小的节点个数。
if(p->key==tkey) return p->ch[0]->size+res+1; //这里返回的是最小排名,实际上排名范围为[ p->ch[0]->size+res+1 , p->ch[0]->size+res+p->cnt ]
if(tkeykey) return _Rank(p->ch[0],tkey,res);
return _Rank(p->ch[1],tkey,res+ p->ch[0]->size + p->cnt);
} 求前驱(Pred)和后继(Succ):
很常用的询问,实际上就相当于二分的效果。注意这里的前驱定义为Treap中的元素中小于tkey,且最大的值,后继定义为大于tkey,且最小的数,当然tkey不一定是Treap里的元素。解决这两个问题的主要思路就是通过tkey与p->的大小关系来缩小范围求出最优的。
int _Pred(P_node p,int tkey){
if(p==null) return -1e+9;
if(tkey<=p->key) return _Pred(p->ch[0],tkey); //比tkey小的在左边
return max(p->key,_Pred(p->ch[1],tkey)); //p->key < tkey;p比p的左子树优秀,左子树不用看了,加入p并在右子树中找。
}
int _Succ(P_node p,int tkey){ //道理和上面一样
if(p==null) return 1e+9;
if(tkey>=p->key) return _Succ(p->ch[1],tkey);
return min(p->key,_Succ(p->ch[0],tkey));
} 完整模板:
#includestruct Treap{
node base[maxn],nil;
P_node root,null,len;
Treap(){
root=null=&nil;
null->key=null->fix=1e+9;
null->size=null->cnt=0;
null->ch[0]=null->ch[1]=null;
len=base;
}
P_node newnode(int tkey){
len->key=tkey; len->fix=rand();
len->ch[0]=len->ch[1]=null;
len->size=len->cnt=1;
return len++;
}
void rot(P_node &p,int d){
P_node k=p->ch[d^1]; p->ch[d^1]=k->ch[d]; k->ch[d]=p;
p->maintain(); k->maintain(); p=k;
}
void _Insert(P_node &p,int tkey){
if(p==null) p=newnode(tkey); else
if(p->key==tkey) p->cnt++; else{
int d=tkey>p->key;
_Insert(p->ch[d],tkey); if(p->ch[d]->fix > p->fix) rot(p,d^1);
}
p->maintain();
}
void _Erase(P_node &p,int tkey){
if(p->key==tkey){
if(p->cnt>1) p->cnt--; else
if(p->ch[0]==null) p=p->ch[1]; else
if(p->ch[1]==null) p=p->ch[0]; else{
int d=p->ch[0]->fix > p->ch[1]->fix;
rot(p,d); _Erase(p->ch[d],tkey);
}
} else _Erase(p->ch[tkey>p->key],tkey);
p->maintain();
}
int _Kth(P_node p,int k){
if(p==null||k<1||k>p->size) return 0;
if(kch[0]->size+1) return _Kth(p->ch[0],k);
if(k>p->ch[0]->size+p->cnt) return _Kth(p->ch[1],k-p->ch[0]->size-p->cnt);
return p->key;
}
int _Rank(P_node p,int tkey,int res){
if(p->key==tkey) return p->ch[0]->size+res+1;
if(tkeykey) return _Rank(p->ch[0],tkey,res);
return _Rank(p->ch[1],tkey,res+ p->ch[0]->size + p->cnt);
}
int _Pred(P_node p,int tkey){
if(p==null) return -1e+9;
if(tkey<=p->key) return _Pred(p->ch[0],tkey);
return max(p->key,_Pred(p->ch[1],tkey));
}
int _Succ(P_node p,int tkey){
if(p==null) return 1e+9;
if(tkey>=p->key) return _Succ(p->ch[1],tkey);
return min(p->key,_Succ(p->ch[0],tkey));
}
void _Print(P_node p){
if(p==null) return;
_Print(p->ch[0]);
for(int i=1;i<=p->cnt;i++) printf("%d ",p->key);
_Print(p->ch[1]);
}
void Insert(int tkey){ _Insert(root,tkey); }
void Erase(int tkey){ _Erase(root,tkey); }
int Kth(int k){ return _Kth(root,k); }
int Rank(int tkey){ return _Rank(root,tkey,0); }
int Pred(int tkey){ return _Pred(root,tkey); }
int Succ(int tkey){ return _Succ(root,tkey); }
void Print(){ _Print(root); printf("\n"); }
} T;
int n;
int main(){
freopen("treap.in","r",stdin);
freopen("treap.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++){
int pd,x; scanf("%d%d",&pd,&x);
if(pd==1) T.Insert(x);
if(pd==2) T.Erase(x);
if(pd==3) printf("%d\n",T.Rank(x));
if(pd==4) printf("%d\n",T.Kth(x));
if(pd==5) printf("%d\n",T.Pred(x));
if(pd==6) printf("%d\n",T.Succ(x));
}
return 0;
}