题目描述
不到长城非好汉,但是不是每个人都能轻易的登上长城的。
因为只有解开 $LCM(k^{2^l}+1,k^{2^{(l+1)}}+1, ……,k^{2^r}+1)$ 这道题的人才能登上。其中k,l,r是给定的整数。由于结果比较大,我们将结果对p取余,p是一个质数。
说明:
$LCM(a_1,a_2,…,a_n)$ 表示的是 $a_1,a_2,…,a_n$ 的最小公倍数。
我们规定,对于任意整数x, $x^0=1$ ;
不到长城非好汉,但是不是每个人都能轻易的登上长城的。
因为只有解开 LCM(k2l+1,k2(l+1)+1,……,k2r+1)LCM(k2l+1,k2(l+1)+1,……,k2r+1)
这道题的人才能登上。其中k,l,r是给定的整数。由于结果比较大,我们将结果对p取余,p是一个质数。
说明:
LCM(a1,a2,…,an)LCM(a1,a2,…,an)
表示的是 a1,a2,…,ana1,a2,…,an
的最小公倍数。
我们规定,对于任意整数x, x0=1x0=1
;
** 收起
** 展开全文
**
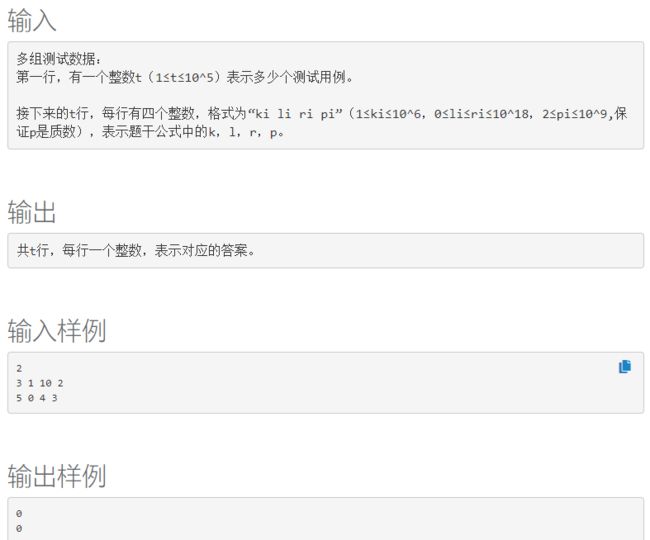
输入
```{.ng-binding style="font-size: medium; word-wrap: break-word; white-space: pre-wrap;"}
多组测试数据:
第一行,有一个整数t(1≤t≤10^5)表示多少个测试用例。
接下来的t行,每行有四个整数,格式为“ki li ri pi”(1≤ki≤10^6,0≤li≤ri≤10^18,2≤pi≤10^9,保证p是质数),表示题干公式中的k,l,r,p。
```
输出
{.ng-binding style="font-size: medium; word-wrap: break-word; white-space: pre-wrap;"} 共t行,每行一个整数,表示对应的答案。
输入样例
2
3 1 10 2
5 0 4 3输出样例
0
0**
BB
痛失一血(打了场Comet OJ回来就没了)
不过后来又刷了一道水题
题解
LCM+取模=结论题
结论1
$gcd(k^{2^i}+1,k^{2^j}+1)=1 (i\neq j 且k为偶数)$
证明:
设i 若存在$q\mid k^{2^i}+1$,则$k^{2^i}\equiv -1(mod ;q)$ 那么$k^{2^{i+k}}\equiv 1(mod ;q)$(k>0),则$k^{2^j} \equiv 1(mod ;q)$,$k^{2^j}+1 \equiv 2(mod ;q)$ 当q>2时无解,当q=2时由于k为偶数,所以k的幂+1为奇数,不存在为2的因子(即无解) 所以gcd=1 gcd(k^{2^i}+1,k^{2^j}+1)=2 (i\neq j 且k为奇数)$ 证明: 同上,可以发现只存在q=2的公因数 简单又自然 先特判掉模数为2 ①K不是P的倍数 如果K不是P的倍数,那么把式子拆开后变成 $ans=\sum_{i=0}^{2^{r-l+1}-1}{({k^{2^l}})^i}$ 设$a={k^{2^l}}$,则$ans=\sum_{i=0}^{2^{r-l+1}-1}{a^i}$ 2^l^和$2^r$可以快速幂求,因为a^0^=a^p-1^ mod p=1,可以发现模数实际上是(P-1) 剩下的就是一个等比数列求和 因为K不是P的倍数且P为质数,所以$k^{2^{i}}$必定不为0,$k^{2^{i}}-1$(等比数列求和的分母)不会为-1 但是$k^{2^{i}}$可能为1,这样的话$ans=2^{r-l+1}$ ②K是P的倍数 显然ans=1 如果K为奇数,那么就还要除掉多出来的的2^R-L^结论2
乱搞
code
#include