算法设计与分析——全排列问题算法分析(递归调用分析图)
(目前网上最易理解递归调用的分析过程——递归调用分析图)
全排列:
从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。
例如:
1 、2 、3三个元素的全排列为:
{1,2,3},{1,3,2},{2,1,3},{2,3,1},{3,1,2},{3,2,1}。
算法思路分析:
设R={r1,r2,…,rn}是要进行排列的n个元素,Ri=R-{ri}。集合X中元素的全排列记为Perm(X)。(ri)Perm(X)表示在全排列Perm(X)的每一个排列前加上前缀ri得到的排列。R的全排列可归纳定义如下:
当n=1时,Perm(R)=(r),其中r是集合R中唯一的元素;
当n>1时,Perm(R)由(r1)Perm(R1),(r2)Perm(R2),…,(rn)Perm(Rn)构成。
依此递归定义,可设计产生Perm(R)的递归算法如下:
template
void Perm(Type list[], int k, int m)
{//产生list[k:m]的所有排列
if(k == m)
{//只剩下一个元素
for(int i = 0; i <= m; i++)
cout << list[i];
cout << endl;
}
else//还有多个元素待排列,递归产生排列
for(int i = k; i <= m; i++)
{
Swap(list[k], list[i]);
Perm(lsit, k+1, m);
Swap(list[k], list[i]);
}
}
template
inline void Swap(Type& a, Type& b)
{
Type temp = a;
a = b;
b = temp;
} 算法Perm(list,k,m)递归地产生所有前缀是list[0:k-1],且后缀是list[k:m]的全排列的所有排列。函数调用Perm(list,0,n-1)则产生list[0:n-1]的全排列。
在一般情况下,k<m。算法将list[k:m]中的每一个元素分别与list[k ]中的元素交换。然后递归地计算list[k+1:m]的全排列,并将计算结果作为list[0:k]的后缀算法中Swap是用于交换两个变量值的内联函数。
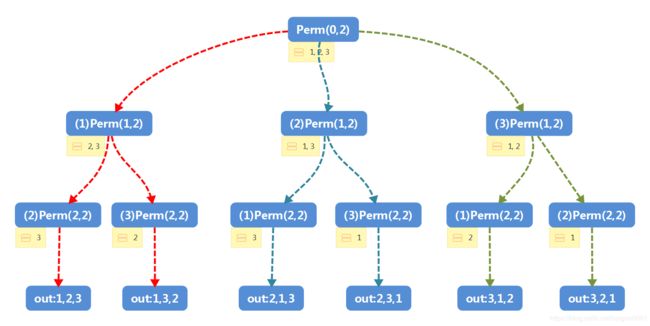
此递归思路不好理解,我们分析一下元素{1, 2, 3},Perm(0,2)的递归调用图:
Java代码参考:
//注意:此代码缺点,不能去除重复元素的全排列
import java.util.Arrays;
public class PermDemo0
{
static int[] list = {1, 2, 3};
public static void main(String[] args)
{
Perm(list, 0);
}
public static void Perm(int[] list, int start)
{
if(start == list.length-1)
System.out.println(Arrays.toString(list));
else
{
for(int i = start; i <= list.length-1; i++)
{
Swap(list, start, i);
Perm(list, start+1);
Swap(list, start, i);
}
}
}
public static void Swap(int[] list, int i, int j)
{
int temp = list[i];
list[i] = list[j];
list[j] = temp;
}
}
/*
[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 2, 1]
[3, 1, 2]
*/
去重复元素的递归调用图(特别注意k,i的值):
//代码优化,去除重复元素的全排列
import java.util.Arrays;
public class PermDemo1
{
static int[] list = {1, 2, 2};
public static void main(String[] args)
{
Perm(list, 0);
}
public static void Perm(int[] list, int start)
{
if(start == list.length-1)
{
System.out.println(Arrays.toString(list));
}
else
{
for(int i = start; i <= list.length-1; i++)
{
if(!Overlap(list, start, i))
{
break;
}
Swap(list, start, i);
Perm(list, start+1);
Swap(list, start, i);
}
}
}
public static void Swap(int[] list, int i, int j)
{
int temp = list[i];
list[i] = list[j];
list[j] = temp;
}
public static boolean Overlap(int[] list, int start, int i)
{
for (int j = start; j < i; j++)
{
/**
* a[i] 是等待被交换的元素
* 如果 start == i 需要进行交换
* 如果 在 [start, i) 范围里存在和 a[i] 相同的元素则不进行交换,说明这种情况已经存在了
*/
if (list[j] == list[i])
{
return false;
}
}
return true;
}
}
/*
[1, 2, 2]
[2, 1, 2]
[2, 2, 1]
*///代码优化,去除重复元素的全排列
import java.util.Arrays;
public class PermDemo1
{
static int[] list = {1, 2, 2, 2};
public static void main(String[] args)
{
Perm(list, 0);
}
public static void Perm(int[] list, int start)
{
if(start == list.length-1)
{
System.out.println(Arrays.toString(list));
}
else
{
for(int i = start; i <= list.length-1; i++)
{
if(!Overlap(list, start, i))
{
break;
}
Swap(list, start, i);
Perm(list, start+1);
Swap(list, start, i);
}
}
}
public static void Swap(int[] list, int i, int j)
{
int temp = list[i];
list[i] = list[j];
list[j] = temp;
}
public static boolean Overlap(int[] list, int start, int i)
{
for (int j = start; j < i; j++)
{
/**
* a[i] 是等待被交换的元素
* 如果 start == i 需要进行交换
* 如果 在 [start, i) 范围里存在和 a[i] 相同的元素则不进行交换,说明这种情况已经存在了
*/
if (list[j] == list[i])
{
return false;
}
}
return true;
}
}
/*
[1, 2, 2, 2]
[2, 1, 2, 2]
[2, 2, 1, 2]
[2, 2, 2, 1]
*/
参考资料:
计算机算法设计与分析(第4版) 王晓东 著
https://blog.csdn.net/jiaobuchong/article/details/85369970
https://blog.csdn.net/morewindows/article/details/7370155
https://blog.csdn.net/lemon_tree12138/article/details/50986990