【机器学习笔记】——感知机(Perceptron)
目 录
- 1 感知机(Perceptron)
- 1.1 定义
- 1.2 几何解释
- 1.3 学习策略
- 1.4 算法
- 1.4.1 原始形式
- 1.4.2 对偶形式
- 1.5 感知机 Vs 支持向量机
- 2 算法实现
- 2.1 实现原始形式算法
- 2.2 实现对偶形式算法
- 2.3 sklearn练习——自定义数据二分类
- 2.4 对比练习——鸢尾花数据分类
- 2.4.1 鸢尾花数据集
- 2.4.2 数据预处理与特征选择
- 2.4.3 对比手写模型与sklearn效果
- 2.4.3.1 准备训练数据
- 2.4.3.2 手写模型训练
- 2.4.3.3 结果查看
- 2.4.3.4 与sklearn结果对比
- 3 参考文献
1 感知机(Perceptron)
感知机是二类分类的线性分类模型,旨在求出将训练数据进行线性划分的分离超平面,因此导入基于误分类的损失函数,利用梯度下降法对损失函数进行极小化,求得感知机模型。
1.1 定义
假设输入空间是 X ⊆ R n \mathcal{X} \subseteq \mathbf{R}^n X⊆Rn ,输出空间是 Y = { + 1 , − 1 } \mathcal{Y} = \left\{+1,-1\right\} Y={+1,−1} 。输入 x ∈ X x \in \mathcal{X} x∈X 表示实例的特征向量,对应于输入空间的点;输出 y ∈ Y y \in \mathcal{Y} y∈Y 表示实例的类别。由输入空间到输出空间的如下函数
f ( x ) = s i g n ( w ⋅ x + b ) f(x) = sign(w \cdot x + b) f(x)=sign(w⋅x+b)
称为感知机。其中, w ∈ R n w \in \mathbf{R}^n w∈Rn 叫做权值(weight)或权值向量(weight vector), b ∈ R b \in \mathbf{R} b∈R 叫做偏置(bias)。 s i g n sign sign 是符号函数,即
s i g n ( x ) = { + 1 , x ≥ 0 − 1 , x < 0 sign(x) = \begin{cases} +1, & x \ge 0 \\ -1, & x \lt 0 \end{cases} sign(x)={+1,−1,x≥0x<0
1.2 几何解释
线性方程
w ⋅ x + b = 0 w \cdot x + b = 0 w⋅x+b=0
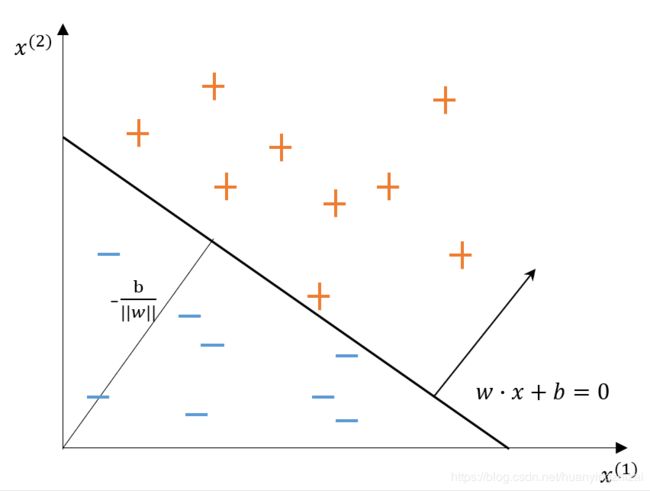
对于特征空间 R n \mathbf{R}^n Rn 中的一个超平面 S ,其中 w w w 是超平面的法向量, b b b 是超平面的截距。这个超平面将特征空间划分为两个部分。位于两部分的点(特征向量)分别被分为正、负两类。因此超平面 S S S 称为分离超平面,如图所示
感知机通过训练训练集数据求得感知机模型,即求得模型参数 w w w , b b b 。通过学习得到的感知机模型,对于新的输入实例给出其对应的输出类别。
1.3 学习策略
假设训练数据集是线性可分的,我们需要找到一个前面所说的分离超平面,即确定感知机模型参数 w w w , b b b 。这需要制定一个学习策略,即定义损失函数并将损失函数极小化。
首先考虑误分点总数,但因其不是参数 w w w , b b b 的连续可导函数,不易优化,因此选择误分点到超平面 S S S 的总距离。我们知道一个点 x 0 x_0 x0 到平面 w ⋅ x + b w \cdot x + b w⋅x+b 的距离 d d d 为 1 ∣ ∣ w ∣ ∣ ∣ w ⋅ x 0 + b ∣ \frac{1}{||w||}| w \cdot x_0 + b | ∣∣w∣∣1∣w⋅x0+b∣ ,对于误分点 ( x i , y i ) (x_i,y_i) (xi,yi) 来说,当 w ⋅ x i + b > 0 w \cdot x_i + b \gt 0 w⋅xi+b>0 时, y i = − 1 y_i = -1 yi=−1 ;当 w ⋅ x i + b < 0 w \cdot x_i + b \lt 0 w⋅xi+b<0 时, y i = + 1 y_i = +1 yi=+1 。所以有:
− y i ( w ⋅ x i + b ) > 0 -y_i (w \cdot x_i + b) \gt 0 −yi(w⋅xi+b)>0
于是误分点到超平面 S S S 的距离为:
− 1 ∣ ∣ w ∣ ∣ y i ( w ⋅ x 0 + b ) -\frac{1}{||w||}y_i(w \cdot x_0 + b) −∣∣w∣∣1yi(w⋅x0+b)
假设超平面 S S S 的误分点集合为 M M M ,那么误分点到超平面 S S S 的总距离为:
− 1 ∣ ∣ w ∣ ∣ ∑ x i ∈ M y i ( w ⋅ x i + b ) -\frac{1}{||w||} \sum_{x_i \in M} y_i (w \cdot x_i + b) −∣∣w∣∣1xi∈M∑yi(w⋅xi+b)
因为 w w w 的大小 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣ 不会影响极小化的结果,因此,忽略 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1 就得到感知及学习的损失函数:
L o s s ( w , b ) = − ∑ x i ∈ M y i ( w ⋅ x i + b ) Loss(w, b) = - \sum_{x_i \in M} y_i (w \cdot x_i + b) Loss(w,b)=−xi∈M∑yi(w⋅xi+b)
1.4 算法
1.4.1 原始形式
感知机学习算法是误分类驱动的,采用随机梯度下降(SGD)法极小化损失函数。首先任意选取一个超平面 S 0 S_0 S0 (即初始化模型参数 w 0 w_0 w0 , b 0 b_0 b0 ),然后随机选取一个误分类点(遍历数据集找到误分类的点)使其梯度下降(见CH12_2):
∇ w L ( w , b ) = − ∑ x i ∈ M y i x i \nabla_w L(w, b) = -\sum_{x_i \in M}y_i x_i ∇wL(w,b)=−xi∈M∑yixi
∇ b L ( w , b ) = − ∑ x i ∈ M y i \nabla_b L(w, b) = -\sum_{x_i \in M}y_i ∇bL(w,b)=−xi∈M∑yi
对于误分类点 ( x i , y i ) (x_i, y_i) (xi,yi) ,对 w w w , b b b 进行更新:
w ← w − η ∇ w , x i L ( w , b ) = w + η y i x i w \gets w - \eta \nabla_{w, x_i} L(w, b) = w + \eta y_i x_i w←w−η∇w,xiL(w,b)=w+ηyixi
b ← b − η ∇ w , x i L ( w , b ) = w + η y i b \gets b - \eta \nabla_{w, x_i} L(w, b) = w + \eta y_i b←b−η∇w,xiL(w,b)=w+ηyi
重复执行上述步骤直到一次更新后不再有误分类点。而且由于初值和误分类点的选择顺序不同,最终结果可以有无穷多个。其实这很容易理解,考虑平面上线性可分的数据集,当然存在无穷多个超平面可以将其分开。另外可以证明误分类的次数是有上届的,经过有限次搜索可以找到将训练数据集完全分开的超平面,也就是说,当训练数据集线性可分时,感知机学习算法原始形式迭代是收敛的。算法的伪代码如下:
输入:训练数据集 T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) T={(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)} T=(x1,y1),(x2,y2),⋯,(xN,yN),其中 x i ∈ X = R n x_i\in \mathcal{X}=\mathbf{R}^n xi∈X=Rn, y i ∈ Y = − 1 , + 1 y_i\in \mathcal{Y}={-1, +1} yi∈Y=−1,+1, i = 1 , 2... N i=1,2...N i=1,2...N,学习速率为 η \eta η( 0 < η ≤ 1 0\lt \eta \le 1 0<η≤1)
输出: w w w, b b b;感知机模型 f ( x ) = s i g n ( w ⋅ x + b ) f(x)=sign(w\cdot x+b) f(x)=sign(w⋅x+b)
(1) 选取初值 w = w 0 w = w_0 w=w0, b = b 0 b = b_0 b=b0,权值可以初始化为0或一个很小的随机数
(2) 在训练数据集中选取 ( x i , y i ) (x_i, y_i) (xi,yi)
(3) 如果 y i ( w ⋅ x i + b ) ≤ 0 y_i(w\cdot x_i+b)\le0 yi(w⋅xi+b)≤0,即该点是误分类点:
w ← w + η y i x i w \gets w + \eta y_ix_i w←w+ηyixi
b ← b + η y i b \gets b + \eta y_i b←b+ηyi
(4) 转至(2),直至训练集中没有误分类点
1.4.2 对偶形式
原始形式中,对于每个误分类点 ( x i , y i ) (x_i, y_i) (xi,yi) ,其需要经过 n i n_i ni 次迭代才能被正确分类, n i n_i ni 越大说明该点距离分离超平面越近,也就越难正确分类。原始形式中,参数的更新为:
w ← w + η y i x i w \gets w + \eta y_i x_i w←w+ηyixi
b ← w + η y i b \gets w + \eta y_i b←w+ηyi
我们令 α i = n i η \alpha_i = n_i \eta αi=niη ,并初始化参数 w 0 = 0 w_0 = 0 w0=0 , b 0 = 0 b_0 = 0 b0=0 。那么最后学习到的 w w w , b b b 为:
w = ∑ i = 1 N α i y i x i w = \sum_{i = 1}^{N} \alpha_i y_i x_i w=i=1∑Nαiyixi
b = ∑ i = 1 N α i y i b = \sum_{i = 1}^{N} \alpha_i y_i b=i=1∑Nαiyi
这样每次迭代时,仅更新 α i \alpha_i αi 和 b b b 即可:
α i ← α i + η \alpha_i \gets \alpha_i + \eta αi←αi+η
b ← w + η y i b \gets w + \eta y_i b←w+ηyi
相比原始形式,对偶形式固定了初始权值,实例仅以 x i y i x_i y_i xiyi 和 y i y_i yi 出现,所以可以提前计算内积 x y xy xy 并以矩阵形式存储(即Gram矩阵),这可以节省空间并提高计算速度。算法的伪代码如下:
输入:训练数据集 T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) T={(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)} T=(x1,y1),(x2,y2),⋯,(xN,yN),其中 x i ∈ X = R n x_i\in \mathcal{X}=\mathbf{R}^n xi∈X=Rn, y i ∈ Y = − 1 , + 1 y_i\in \mathcal{Y}={-1, +1} yi∈Y=−1,+1, i = 1 , 2... N i=1,2...N i=1,2...N,学习速率为 η \eta η( 0 < η ≤ 1 0\lt \eta \le 1 0<η≤1)
输出: α ⃗ \vec{\alpha} α, b b b;感知机模型 f ( x ) = s i g n ( ∑ i = 1 N α i y i x i ⋅ x + b ) f(x)=sign(\sum_{i = 1}^{N}\alpha_i y_i x_i \cdot x+b) f(x)=sign(∑i=1Nαiyixi⋅x+b),其中 α ⃗ = ( α 1 , α 2 , ⋯ , α N ) \vec{\alpha} = (\alpha_1, \alpha_2, \cdots, \alpha_N) α=(α1,α2,⋯,αN)
(1) 选取初值 α ⃗ = 0 ⃗ \vec{\alpha} = \vec{0} α=0, b = 0 b = 0 b=0
(2) 在训练数据集中选取 ( x i , y i ) (x_i, y_i) (xi,yi)
(3) 如果 y i ( ∑ i = 1 N α i y i x i ⋅ x i + b ) ≤ 0 y_i(\sum_{i = 1}^{N}\alpha_i y_i x_i \cdot x_i+b)\le0 yi(∑i=1Nαiyixi⋅xi+b)≤0,即该点是误分类点:
α i ← α i + η \alpha_i \gets \alpha_i + \eta αi←αi+η
b ← w + η y i b \gets w + \eta y_i b←w+ηyi
(4) 转至(2),直至训练集中没有误分类点
1.5 感知机 Vs 支持向量机
-
前者最大程度追求正确划分,最小化错误,容易发生过拟合;后者尽量同时避免过拟合
-
前者的学习策略是最小化损失函数并使用梯度下降法;后者采用的是利用不等式的约束条件构造拉格朗日函数并求极值
-
前者无最优解,或者说解不唯一
2 算法实现
2.1 实现原始形式算法
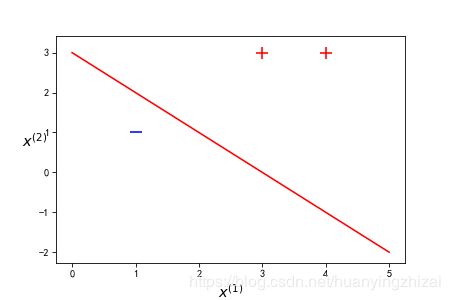
已知正实例点 x 1 = ( 3 , 3 ) T x_1 = (3,3)^T x1=(3,3)T, x 2 = ( 4 , 3 ) T x_2 = (4,3)^T x2=(4,3)T,负实例点 x 3 = ( 1 , 1 ) T x_3 = (1,1)^T x3=(1,1)T,试用感知机学习算法求感知机模型 f ( x ) = s i g n ( w ⋅ x + b ) f(x) = sign(w\cdot x + b) f(x)=sign(w⋅x+b),其中 w = ( w ( 1 ) , w ( 2 ) ) T w = (w^{(1)},w^{(2)})^T w=(w(1),w(2))T, x = ( x ( 1 ) , x ( 2 ) ) T x = (x^{(1)},x^{(2)})^T x=(x(1),x(2))T
参考:variations的博客
import numpy as np
import matplotlib.pyplot as plt
class showPicture:
'''
超平面可视化
'''
def __init__(self, x, y, w, b):
self.b = b
self.w = w
plt.figure()
plt.title('')
plt.xlabel('$x^{(1)}$', size=14)
plt.ylabel('$x^{(2)}$', size=14, rotation = 0)
# 绘制分离超平面
xData = np.linspace(0, 5, 100)
yData = self.expression(xData)
plt.plot(xData, yData, color='r', label='y1 data')
# 绘制数据点
nums = x.shape[0]
for i in range(nums):
plt.scatter(x[i][0],x[i][1], c = 'r' if y[i] == 1 else 'b', marker = '+' if y[i] == 1 else '_', s = 150)
plt.savefig('img/perceptron/incomplement01.png',dpi=75)
def expression(self,x):
'''
根据模型参数预测新的数据点的分类结果
'''
y = (-self.b - self.w[0]*x)/self.w[1]
return y
def show(self):
plt.show()
class perceptron:
'''
感知机模型
'''
def __init__(self,x,y,a=1):
'''
训练数据集X,Y
学习率a设置为1
'''
self.x = x
self.y = y
self.w = np.zeros((x.shape[1],1)) # 选取初值w0,b0
self.b = 0
self.a = 1
def sign(self,w,b,x):
'''
定义符号函数
'''
y = np.dot(x,w)+b
return int(y)
def train(self, logprint = False):
'''
训练感知机模型
logprint:是否打印每次迭代结果,默认不打印
'''
flag = True
length = len(self.x)
while flag:
count = 0 # 迭代控制
for i in range(length):
tmpY = self.sign(self.w,self.b,self.x[i,:])
if tmpY*self.y[i]<=0: # 若数据被误分类
tmp = self.y[i]*self.a*self.x[i,:]
tmp = tmp.reshape(self.w.shape) # 梯度下降ayi_x_i存储为列向量
self.w = tmp +self.w # 权值更新
self.b = self.b + self.y[i] # 偏置更新
count +=1
if logprint == True: # 打印日志
print('第%d次迭代:\n更新后参数 w 为%f,b 为%f' %(count, self.w, self.b))
if count == 0:
flag = False # 无误分退出迭代
return self.w,self.b
x = np.array([3, 3, 4, 3, 1, 1]).reshape(3, 2)
y = np.array([1, 1, -1])
testp = perceptron(x, y)
w, b = testp.train()
tests = showPicture(x, y, w, b)
2.2 实现对偶形式算法
已知正实例点 x 1 = ( 3 , 3 ) T x_1 = (3,3)^T x1=(3,3)T, x 2 = ( 4 , 3 ) T x_2 = (4,3)^T x2=(4,3)T,负实例点 x 3 = ( 1 , 1 ) T x_3 = (1,1)^T x3=(1,1)T,试用感知机学习算法求感知机模型 f ( x ) = s i g n ( w ⋅ x + b ) f(x) = sign(w\cdot x + b) f(x)=sign(w⋅x+b),其中 w = ( w ( 1 ) , w ( 2 ) ) T w = (w^{(1)},w^{(2)})^T w=(w(1),w(2))T, x = ( x ( 1 ) , x ( 2 ) ) T x = (x^{(1)},x^{(2)})^T x=(x(1),x(2))T
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.axisartist as AA
class myperceptron2:
def __init__(self, x, y, eta = 1):
self.x = x
self.y = y
self.n = np.zeros(x.shape[0])
self.eta = 1
# 求Gram矩阵
def gram(self):
g = []
for i in self.x:
for j in self.x:
g.append(np.dot(i, j)) # 这里浪费存储空间
return np.array(g).reshape(self.x.shape[0], self.x.shape[0])
def train(self):
flag = True
while flag:
count = 0
for i in range(len(self.x)):
if self.y[i]*(np.sum([self.n[j]*self.eta*self.y[j]*(self.gram()[i][j]+1) for j in range(len(self.x))])) <= 0:
self.n[i] += 1
count += 1
if count==0:
flag = False
w = np.add.reduce([self.n[i]*self.eta*self.y[i]*self.x[i] for i in range(len(self.x))]).reshape((self.x.shape[1], 1))
b = np.sum([self.n[i]*self.eta*self.y[i] for i in range(len(self.y))])
return w, b
def showPicture2(x, y, w, b):
fig = plt.figure()
# 坐标轴设置
ax = AA.Subplot(fig, 111) # 使用axisartist.Subplot方法创建一个绘图区对象ax
fig.add_axes(ax) # 将绘图区对象添加到画布中
ax.axis[:].set_visible(False) # 通过set_visible方法设置绘图区所有坐标轴隐藏
ax.axis["x"] = ax.new_floating_axis(0,0) # 添加x轴
ax.axis["x"].set_axisline_style("-|>", size = 1.0) # 给x坐标轴加上箭头
ax.axis["x"].set_axis_direction("bottom") # 设置x轴数字标签在轴下面
ax.axis["x"].label.set_text("$x^{(1)}$")
ax.axis["x"].label.set_fontsize(14)
ax.set_xlim(-0.1, 5.5)
ax.axis["y"] = ax.new_floating_axis(1,0)
ax.axis["y"].set_axisline_style("-|>", size = 1.0)
ax.axis["y"].set_axis_direction("left")
ax.axis["y"].label.set_text("$x^{(2)}$")
ax.axis["y"].label.set_rotation(90)
ax.axis["y"].label.set_fontsize(14)
ax.set_ylim(-1.1, 3.5)
# 添加公式
w1, w2 = w[0][0], w[1][0]
if (w1==1) & (w2 == 1):
if b != 0:
ax.text(3, 0.5, "%s$x^{(1)}$+%s$x^{(2)}$%+i = 0" %('', '', b), color = 'black', fontsize = 14)
else:
ax.text(3, 0.5, "%s$x^{(1)}$+%s$x^{(2)}$ = 0" %('', ''), color = 'black', fontsize = 14)
elif w1==-1 & w2 == 1:
if b != 0:
ax.text(3, 0.5, "-%s$x^{(1)}$+%s$x^{(2)}$%+i = 0" %('', '', b), color = 'black', fontsize = 14)
else:
ax.text(3, 0.5, "-%s$x^{(1)}$+%s$x^{(2)}$ = 0" %('', ''), color = 'black', fontsize = 14)
elif w1==-1 & w2 == -1:
if b != 0:
ax.text(3, 0.5, "-%s$x^{(1)}$-%s$x^{(2)}$%+i = 0" %('', '', b), color = 'black', fontsize = 14)
else:
ax.text(3, 0.5, "-%s$x^{(1)}$-%s$x^{(2)}$ = 0" %('', ''), color = 'black', fontsize = 14)
elif w1==1 & w2 == 1:
if b != 0:
ax.text(3, 0.5, "%s$x^{(1)}$+%s$x^{(2)}$%+i = 0" %('', '', b), color = 'black', fontsize = 14)
else:
ax.text(3, 0.5, "%s$x^{(1)}$+%s$x^{(2)}$ = 0" %('', ''), color = 'black', fontsize = 14)
else:
if b != 0:
ax.text(3, 0.5, "%i$x^{(1)}$%+i$x^{(2)}$%+i = 0" %(w1, w2, b), color = 'black', fontsize = 14)
else:
ax.text(3, 0.5, "%i$x^{(1)}$%+i$x^{(2)}$ = 0" %(w1, w2), color = 'black', fontsize = 14)
# 绘制分离超平面
lx = np.arange(0, 5, 0.05)
ly = (-b - w[0][0]*lx)/w[1][0]
plt.plot(lx, ly, c='black')
# 添加数据点
for i in range(len(x)):
m = '+' if y[i] == 1 else '_'
plt.scatter(x[i][0], x[i][1], marker = m, s = 150)
ax.text(x[i][0], x[i][1]+0.2, "$x_{0}$".format(str(i+1)), color = 'black', fontsize = 14)
plt.savefig('img/perceptron/imcomplement02.png',dpi=75)
x = np.array([3, 3, 4, 3, 1, 1]).reshape(3, 2)
y = np.array([1, 1, -1])
mytestp = myperceptron2(x, y)
w, b = mytestp.train()
showPicture2(x, y, w, b)
2.3 sklearn练习——自定义数据二分类
sklearn.linear_model.Perceptron参数列表:
| 参数 | 参数类型 | 参数解释 |
|---|---|---|
| penalty | None(默认不加惩罚), ‘l2’(L2正则) or ‘l1’(L1正则) or ‘elasticnet’(混合正则) | 惩罚项 |
| alpha | float(默认0.0001) | 正则化参数 |
| fit_intercept | bool(默认True) | 是否对参数 b b b 进行估计,若为False则数据应是中心化的 |
| max_iter | int(默认1000) | 最大迭代次数 |
| tol | float or None(默认1e-3) | 停止标准,若不指定,训练会在两次迭代损失小于tol时停止 |
| shuffle | bool(默认True) | 每轮训练后是否打乱数据 |
| verbose | integer | verbose = 0 为不在标准输出流输出日志信息; verbose = 1 为输出进度条记录; verbose = 2 为每个epoch输出一行记录 |
| eta0 | double(默认为1) | 学习率 |
| n_jobs | int or None(默认为None) | 在多分类时使用的CPU数量,默认为None(或1),若为-1则使用所有CPU |
| random_state | int, RandomState instance or None(默认None) | 使用shuffle时的随机种子 |
| early_stopping | bool(默认False) | 当验证得分不再提高时是否设置提前停止来终止训练。若设置此项,当验证得分在n_iter_no_change轮内没有提升时提前停止训练 |
| validation_fraction | float(默认0.1) | 验证集比例,只有设置了early_stopping时才有用 |
| n_iter_no_change | int(默认5) | 在提前停止前模型不再提升的次数 |
| class_weight | dict, {class_label: weight} or “balanced” or None | 类别的权重,默认等权重,“balanced”会自动根据数据中的y的各类别数量的反比来调整权重:n_samples / (n_classes * np.bincount(y)) |
| warm_start | bool | 若为True则调用前一次设置的参数,使用新设置的参数 |
sklearn.linear_model.Perceptron属性列表:
| 属性 | 解释 | 类型 |
|---|---|---|
| coef_ | 权值w参数 | array, shape = [1, n_features] if n_classes == 2 else [n_classes, n_features] |
| intercept_ | 偏置b参数 | array, shape = [1] if n_classes == 2 else [n_classes] |
| n_iter_ | 迭代次数 | int |
import numpy as np
from matplotlib import pyplot as plt
from sklearn.datasets import make_classification
from sklearn.linear_model import Perceptron # 导入感知机模型
# 生成分类数据
x,y = make_classification(n_samples=1000,
n_features=2,
n_redundant=0,
n_informative=1,
n_clusters_per_class=1)
x_data_train = x[:800]
x_data_test = x[800:]
y_data_train = y[:800]
y_data_test = y[800:]
# 训练
clf = Perceptron(fit_intercept = False, max_iter = 100, tol = 0.001, shuffle = False, eta0 = 0.1)
clf.fit(x_data_train,y_data_train)
#print(clf.coef_) # w参数
#print(clf.intercept_) # b参数
acc = clf.score(x_data_test,y_data_test) # 使用测试集进行验证
print(acc)
positive_x1 = [x[i,0] for i in range(1000) if y[i] == 1] # 正实例点
positive_x2 = [x[i,1] for i in range(1000) if y[i] == 1]
negetive_x1 = [x[i,0] for i in range(1000) if y[i] == 0] # 负实例点
negetive_x2 = [x[i,1] for i in range(1000) if y[i] == 0]
#画出正例和反例的散点图
fig = plt.figure(dpi = 100)
plt.scatter(positive_x1, positive_x2, c = 'r')
plt.scatter(negetive_x1, negetive_x2, c = 'b')
#画出超平面(在本例中即是一条直线)
line_x = np.arange(-4,4)
line_y = line_x * (-clf.coef_[0][0] / clf.coef_[0][1]) - clf.intercept_
plt.plot(line_x,line_y)
plt.show()
2.4 对比练习——鸢尾花数据分类
参考:AI圈终身学习的博客
2.4.1 鸢尾花数据集
鸢尾花数据集中有三类数据,分别是山鸢尾,变色鸢尾和维吉尼亚鸢尾,各有50个,总共有150个。数据集的特征数据为:
- sepal length(萼片长度)
- sepal width(萼片宽度)
- petal length(花瓣长度)
- petal width(花瓣宽度)
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names) # iris.data包含一个(150, 4)的数据,设置列名为iris.feature_names
df['label'] = iris.target # iris.target为类别标签(150, 1)
df.head()
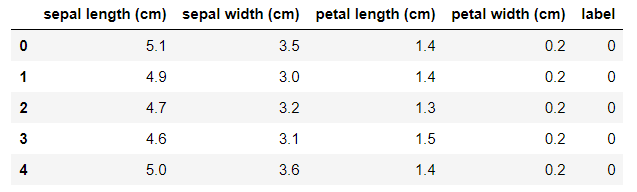
在这个数据集里,特征单位都是厘米(cm),label为0的是山鸢尾, label为1的是变色鸢尾,label为2的是维吉尼亚鸢尾。
由于感知机的线性局限性,他只能做二分类任务。
所以现在我们对数据集进行数据预处理,把label为2的维吉尼亚鸢尾的数据去掉,变成一个识别图片是山鸢尾还是变色鸢尾的二分类任务。
2.4.2 数据预处理与特征选择
数据预处理特别简单,因为数据集的数据是顺序存放的,前50条是label为0的山鸢尾,中间50条是label为1的变色鸢尾,所以我们直接取前100条就好了。
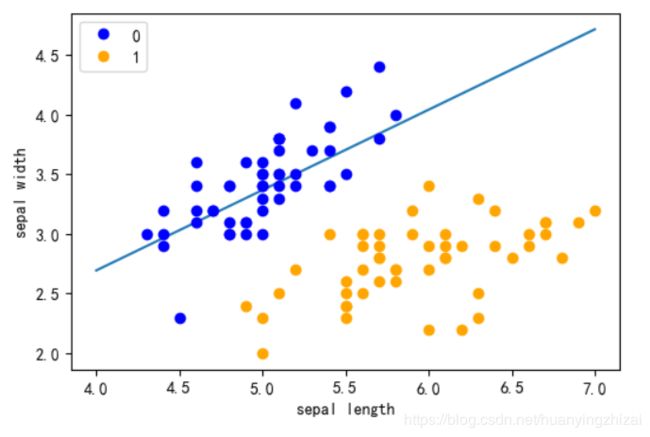
我们在选取之前先对特征进行选择,这里我们只选萼片组[‘sepal length’, ‘sepal width’]作为特征,先看下萼片组[‘sepal length’, ‘sepal width’]和label的相关性:
# 萼片组['sepal length','sepal width']特征分布查看
fig = plt.figure(dpi = 100)
plt.scatter(df[:50]['sepal length (cm)'], df[:50]['sepal width (cm)'], label='0')
plt.scatter(df[50:100]['sepal length (cm)'], df[50:100]['sepal width (cm)'], label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()

可以看到sepal length大概分布在4~7之间,sepal width大概分布在2~5之间
2.4.3 对比手写模型与sklearn效果
2.4.3.1 准备训练数据
我们先把萼片组特征[‘sepal length’, ‘sepal width’]和前100条只包含label=0和label=1的数据取出来:
# 取前100行,第1、2、5列数据为训练集
data = np.array(df.iloc[:100, [0, 1, -1]])
X, y = data[:,:-1], data[:,-1]
2.4.3.2 手写模型训练
class Perceptron(object):
def __init__(self, input_feature_num, activation=None):
self.activation = activation if activation else self.sign
self.w = [0.0] * input_feature_num
self.b = 0.0
def sign(self, z):
# 阶跃激活函数:
# sign(z) = 1 if z > 0
# sign(z) = 0 otherwise
return int(z>0)
def predict(self, x):
# 预测输出函数
# y_hat = f(wx + b)
return self.activation(
np.dot(self.w, x) + self.b)
def fit(self, x_train, y_train, iteration=10, learning_rate=0.1):
# 训练函数
for _ in range(iteration):
for x, y in zip(x_train, y_train):
y_hat = self.predict(x)
self._update_weights(x, y, y_hat, learning_rate)
print(self)
def _update_weights(self, x, y, y_hat, learning_rate):
# 权重更新, 对照公式查看
delta = y - y_hat
self.w = np.add(self.w,
np.multiply(learning_rate * delta, x))
self.b += learning_rate * delta
def __str__(self):
return 'weights: {}\tbias: {}'.format(self.w, self.b)
2.4.3.3 结果查看
perceptron = Perceptron(input_feature_num=X.shape[1])
perceptron.fit(X, y, iteration=1000, learning_rate=0.1)
weights: [ 7.9 -10.07] bias: -12.399999999999972
x_points = np.linspace(4, 7, 10)
y_ = -(perceptron.w[0]*x_points + perceptron.b)/perceptron.w[1]
fig = plt.figure(dpi = 100)
plt.plot(x_points, y_) # 超平面
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()
2.4.3.4 与sklearn结果对比
from sklearn.linear_model import Perceptron
clf = Perceptron(fit_intercept=False, max_iter=1000, tol = 0.0001, shuffle=False, eta0 = 0.1)
clf.fit(X, y)
Perceptron(alpha=0.0001, class_weight=None, early_stopping=False, eta0=0.1,
fit_intercept=False, max_iter=1000, n_iter=None, n_iter_no_change=5,
n_jobs=None, penalty=None, random_state=0, shuffle=False, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
x_points = np.linspace(4, 7, 10)
y_ = -(clf.coef_[0][0]*x_points + clf.intercept_)/clf.coef_[0][1]
fig = plt.figure(dpi = 100)
plt.plot(x_points, y_)
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()
clf.n_iter_ # 实际迭代次数
27
因为sklearn的Perceptron我们设置了迭代的停止标准,所以实际的迭代次数很少使得模型表现不好
3 参考文献
-
《统计学习方法》李航
-
variations的博客
-
诺坎普奇迹的博客
-
AI圈终身学习的博客