K-均值聚类用于实际问题(Matlab实现)
我在上一篇博客中详细介绍了K-均值聚类(K-means)的相关内容,这篇博客基于上一篇博客中的理论,用一个例子介绍如何将K-均值聚类的理论实现到代码中,解决实际问题,编程工具为Matlab 2018b。
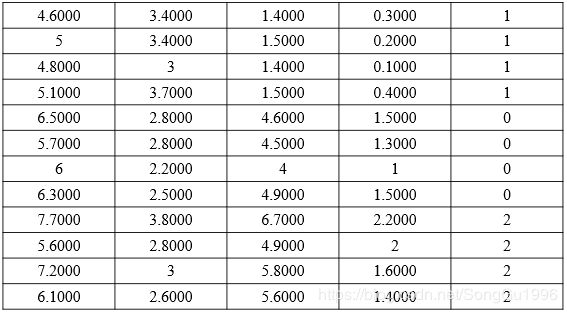
本文使用安德森鸢尾花卉数据集(iris)作为演示的例子,这个数据集中包含150个样本,对应着它的150行,每一行包含着这个样本的4个特征(花萼长度、花萼宽度、花瓣长度、花瓣宽度)和样本的类别标签(0或1或2,它们分别代表不同的品种),所以数据集中存储的是一个尺寸为150×5的二维矩阵,数据集中部分样本的信息如下图所示(最后一列是标签)。由于K-均值聚类是无监督的,所以最后一列的标签仅仅用于评估聚类结果。我们的任务是:求得三个簇中心,将样本划分成三类。
iris数据集我已经上传到百度云,有需要的小伙伴可以自行下载。
链接:https://pan.baidu.com/s/15p8-JOoui8taai0tSADNyA
提取码:k0cs
代码如下:
① 首先定义一个用于计算全部样本点到所有簇中心的欧氏距离的平方的函数
% 输入变量data为样本集,它是一个M×N的矩阵,M代表样本数,N代表特征维度
% 输入变量center为簇中心,它是一个K×N的矩阵,K代表类别数,N代表特征维度
% 输出变量output是一个M×K的矩阵,每一行表示一个样本分别与K个簇中心的欧氏距离的平方
function output = ou_distance(data, center)
% 变量data_num中存放的是样本数量
data_num = size(data, 1);
% 变量center_num中存放的是类别数
center_num = size(center, 1);
% 初始化输出变量
output = zeros(data_num, center_num);
% 求输出变量
for i = 1: center_num
% 求样本集与第i个聚类中心的差值
% 函数repmat的功能是复制矩阵,若B = repmat(A, m, n),则认为B是由m×n块矩阵A平铺而成
difference = data - repmat(center(i,:), data_num, 1);
% 计算欧氏距离的平方
output(:,i) = sum(difference .* difference, 2);
end② 用K-均值聚类求合适的簇中心
% 读取数据集,变量data存储的是一个尺寸为150×5的矩阵,第5列是标签
data = load('iris.data');
% 将样本特征和样本标签分类存放
feature = data(:, 1:4);
label = data(:, 5);
% 对样本特征进行0-1归一化操作
flattened_feature = feature(:)';
mapped_flattened_feature = mapminmax(flattened_feature, 0, 1);
feature = reshape(mapped_flattened_feature, size(feature));
% 变量K中存放的是类别数,本例中K=3
K = 3;
% 从变量feature中随机挑选K个样本作为初始簇中心
% 变量data_num中存放的是样本数量
% 变量temp中存放的是随机产生的K个序号
% 变量center中存放的是挑选出的K个簇中心
data_num = size(feature, 1);
temp = randperm(data_num, K)';
center = feature(temp, :);
% 变量iteration中存放的是迭代次数
iteration = 0;
% 开始迭代
while 1
% 变量distance中存放的是样本特征集与所有簇中心的欧氏距离的平方
% 它是一个M×K的矩阵,M是样本量,K是类别数
distance = ou_distance(feature, center);
% 对变量distance的每一行从小到大排序,变量index中存放的是排序后的序号
[~, index] = sort(distance, 2, 'ascend');
% 计算新的簇中心
center_new = zeros(K, size(feature, 2));
for i = 1:K
class_i_feature = feature(index(:, 1) == i, :);
center_new(i, :) = mean(class_i_feature, 1);
end
% 更新迭代次数
iteration = iteration + 1;
% 输出当前迭代次数
fprintf('当前迭代次数为:%d\n', iteration);
% 如果聚类中心与上一次迭代相同,则停止迭代,跳出循环
if center_new == center
break;
end
% 否则用新的簇中心来取代旧的
center = center_new;
end
% 变量result中存放的是最终的聚类结果
result = index(:, 1);运行上面的代码后,Matlab的命令行中会显示迭代次数,迭代结束后,分类结果保存在变量result中,经过迭代得到的最终的簇中心保存在变量center中,下图左展示的是Matlab命令行中显示的迭代次数,下图右展示的是变量center中的内容,即簇中心。
参考:
https://www.cnblogs.com/yinheyi/p/6132362.html