感知机模型(perceptron)

感知机（perceptron）

  感知机模型属于二分类线性分类模型，属于判别模型和非概率模型。用一句话描述这个模型，就是找到一个超平面，把线性可分数据集分到超平面两侧。

---

线性可分数据集

  存在某个超平面可以将数据集的正实例点和负的实例点完全正确的划分到超平面的两侧，这样的数据集称作线性可分数据集，否则是非线性可分数据集。感知机要求数据集是线性可分的。

---

原始形式

统计学习方法三要素

模型：$y=sign({\omega }^{T}x+b)$
策略：$L(\omega ,b)=\sum _{i\in m}-y_i({\omega }^T{x}_i+b)$，m是误分类的数据集
学习：SGD
$$\frac{\partial L}{\partial \omega }=\sum _{i\in m}-y_i{x}_i,\frac{\partial L}{\partial b}=\sum _{i\in m}-y_i$$
所以参数的更新过程为($\eta 为学习率$)
$$\omega =\omega -\eta \frac{\partial L}{\partial \omega }=\omega +\sum _{i\in m}\eta y_i{x}_i$$
$$b=b-\eta \frac{\partial L}{\partial b}=b+\sum _{i\in m}\eta y_i$$
由于学习方法是随机梯度下降法，所以每次找到一个误分类的$(x_i,y_i)$即可。
  学习算法直观上可以看成，当被选择的实例点位于超平面错误的一侧，则调整$\omega 与b$，使得超平面向该误分类点一侧移动，减小该误分类点到超平面的距离，直至所有超平面都被正确分类。结合下图简单解释一下，假设目前的决策函数位置在${\omega }^{T}x+b=0$处，$x_i$被误分类，由于其在$\omega$指向一侧，所以目标函数把其分类为正(关于超平面知识看我写的SVM里面的超平面部分知识)，实际$y_i=-1$，由于$\eta >0$，$\eta y_i{x}_i$是图上关于$x_i$原点对称点的放缩，假设就在图上表示的点，$\omega$加上$\eta y_i{x}_i$后，$\omega$方向变成${\omega }_2$方向，${\omega }_2$表示的直线假设是图上红线表示的点，可见决策超平面在向着$x_i$能被正确分类的方向转动。

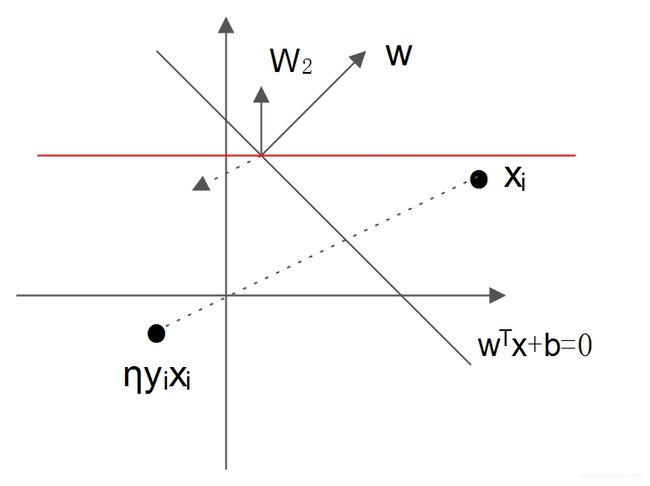
  值得一提的是，在构造感知机的损失函数时，最自然的选择是误分类点的总数，这样的话损失函数长这样$L(\omega ,b)=\sum _{i\in m}-y_{i}sign({\omega }^T{x}_i+b)$，这样的损失函数不是连续可导函数，所以损失函数选择为误分类点到超平面的总距离(在SVM中可知，这种距离称作函数距离)，其对应绝对值损失函数。
  由于学习算法可以采用不同的初值或选取不同的误分类点，最终的感知机模型可能不同。

学习流程

输入：训练集$T=\{(x_1,y_1),(x_2,y_2),(x_3,y_3)\dots (x_n,y_n)\}，\eta (0<\eta \le 1),y_i\in \{-1,1\}$。
输出：$\omega ,b$；决策函数$y=sign(w^{T}x+b)$
执行流程：

1. 初始化参数$\omega 与b$，一般初始化为0。
2. 从训练集中找出一个点$(x_i,y{}_i)$。
3. 如果该点是误分类的点，利用$(x_i,y{}_i)$与公式$\omega =\omega +\eta y_i{x}_i，b=b+\eta y_i$更新参数$\omega 与b$。
4. 重复执行2-3步骤，直到没有误分类的点。

伪代码：

def train(T,n):  #T为数据集，n为步长
    初始化w与b，一般w=0，b=0
    
    do:
        i = 0
        do：
            i += 1
            y = sign(wT·xi+b)
        while(yi·y<0 or i>len(T))
        
        if i <= len(T):
            w = w+nxiyi
            b = b+nyi
    while(i>len(T))
    
    return w,b

---

对偶形式

原理

$从最终结果考虑\omega 与b的更新，表示如下：$
$$\begin{gathered} \omega ={\omega }_{初始化}+\sum _{i=1}^n\eta n_i{y}_i{x}_i={\omega }_{初始化}+\sum _{i=1}^n{\alpha }_i{y}_i{x}_i， \\ {n}_i表示第i条记录用于更新\omega 与b次数。 \end{gathered}$$
$b=b_{初始化}+\sum _{i=1}^n\eta n_i{y}_i=b_{初始化}+\sum _{i=1}^n{\alpha }_i{y}_i，n_i表示第i条记录用于更新\omega 与b次数。$
$$\begin{gathered} 决策函数可以变成y=sign({\omega }^{T}x+b)=sign(\sum _{i=1}^n{\alpha }_i{y}_i{x}_{i}x+b)，{\alpha }_i=\eta n_i， \\ {n}_i表示第i条记录被用于更新模型的次数，这里要求\omega 与b为零初始化。 \end{gathered}$$
$这样我们就把更新\omega 与b变为更新\alpha 与b。$

学习流程

输入：训练集$T=\{(x_1,y_1),(x_2,y_2),(x_3,y_3)\dots (x_n,y_n)\}，\eta (0<\eta \le 1),y_j\in \{-1,1\}$。
输出：${\alpha }_j,b$；决策函数$y=sign(\sum _{j=1}^n{\alpha }_j{y}_j{x}_{j}x+b)$
执行流程
1.$初始化{\alpha }_j=0,j=1\dots n，b=0。$
2.$从训练集中选择一个点(x_i,y_i)。$
3.$$\begin{gathered} 如果该点是误分类的点，则更新{\alpha }_i={\alpha }_i+\eta ，b=b+\eta y_i， \\ 可见b的更新同原始形式一样。 \end{gathered}$$
4.$重复2-3直到没有点被误分类$。
由于在判定一个点是否是误分类的点时，会频繁用到内积$<x_i,x_j>$，所以可以构建一个矩阵保存内积结果，这个矩阵叫做Gram矩阵。

---

参考书籍：《统计学习方法》