常用排序算法总结
概述
在计算器科学与数学中,一个排序算法(英语:Sorting algorithm)是一种能将一串数据依照特定排序方式进行排列的一种算法。本文将总结几类常用的排序算法,包括冒泡排序、选择排序、插入排序、快速排序和归并排序,分别使用Java代码实现,简要使用图例方式介绍其实现原理。
算法原理及实现
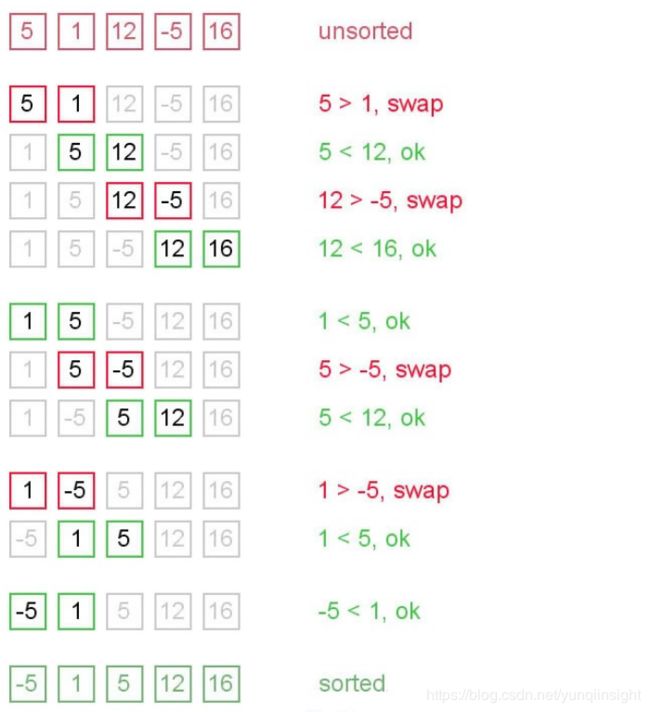
1、冒泡排序
- 原理图
- 理解
通过重复地遍历要排序的列表,比较每对相邻的项目,并在顺序错误的情况下交换它们。
- Java Code
public class BubbleSort {
// logic to sort the elements
public static void bubble_srt(int array[]) {
int n = array.length;
int k;
for (int m = n; m >= 0; m--) {
for (int i = 0; i < n - 1; i++) {
k = i + 1;
if (array[i] > array[k]) {
swapNumbers(i, k, array);
}
}
printNumbers(array);
}
}
private static void swapNumbers(int i, int j, int[] array) {
int temp;
temp = array[i];
array[i] = array[j];
array[j] = temp;
}
private static void printNumbers(int[] input) {
for (int i = 0; i < input.length; i++) {
System.out.print(input[i] + ", ");
}
System.out.println("\n");
}
public static void main(String[] args) {
int[] input = { 4, 2, 9, 6, 23, 12, 34, 0, 1 };
bubble_srt(input);
}
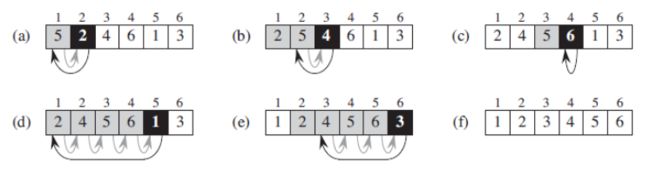
}2、选择排序
- 原理图
- 理解
内部循环查找下一个最小(或最大)值,外部循环将该值放入其适当的位置。
- Java Code
public class SelectionSort {
public static int[] doSelectionSort(int[] arr){
for (int i = 0; i < arr.length - 1; i++)
{
int index = i;
for (int j = i + 1; j < arr.length; j++)
if (arr[j] < arr[index])
index = j;
int smallerNumber = arr[index];
arr[index] = arr[i];
arr[i] = smallerNumber;
}
return arr;
}
public static void main(String a[]){
int[] arr1 = {10,34,2,56,7,67,88,42};
int[] arr2 = doSelectionSort(arr1);
for(int i:arr2){
System.out.print(i);
System.out.print(", ");
}
}
}冒泡排序和选择排序的区别
1、冒泡排序是比较相邻位置的两个数,而选择排序是按顺序比较,找最大值或者最小值;
2、冒泡排序每一轮比较后,位置不对都需要换位置,选择排序每一轮比较都只需要换一次位置;
3、冒泡排序是通过数去找位置,选择排序是给定位置去找数。3、插入排序
- 原理图
- 理解
每一步将一个待排序的记录,插入到前面已经排好序的有序序列中去,直到插完所有元素为止。
- Java Code
public class InsertionSort {
public static void main(String a[]){
int[] arr1 = {10,34,2,56,7,67,88,42};
int[] arr2 = doInsertionSort(arr1);
for(int i:arr2){
System.out.print(i);
System.out.print(", ");
}
}
public static int[] doInsertionSort(int[] input){
int temp;
for (int i = 1; i < input.length; i++) {
for(int j = i ; j > 0 ; j--){
if(input[j] < input[j-1]){
temp = input[j];
input[j] = input[j-1];
input[j-1] = temp;
}
}
}
return input;
}
}4、快速排序
- 原理图
- 理解
将原问题分解为若干个规模更小,但结构与原问题相似的子问题,递归地解这些子问题,然后将这些子问题的解组合为原问题的解。
- Java Code
public class QuickSort {
private int array[];
private int length;
public void sort(int[] inputArr) {
if (inputArr == null || inputArr.length == 0) {
return;
}
this.array = inputArr;
length = inputArr.length;
quickSort(0, length - 1);
}
private void quickSort(int lowerIndex, int higherIndex) {
int i = lowerIndex;
int j = higherIndex;
// calculate pivot number, I am taking pivot as middle index number
int pivot = array[lowerIndex+(higherIndex-lowerIndex)/2];
// Divide into two arrays
while (i <= j) {
/**
* In each iteration, we will identify a number from left side which
* is greater then the pivot value, and also we will identify a number
* from right side which is less then the pivot value. Once the search
* is done, then we exchange both numbers.
*/
while (array[i] < pivot) {
i++;
}
while (array[j] > pivot) {
j--;
}
if (i <= j) {
exchangeNumbers(i, j);
//move index to next position on both sides
i++;
j--;
}
}
// call quickSort() method recursively
if (lowerIndex < j)
quickSort(lowerIndex, j);
if (i < higherIndex)
quickSort(i, higherIndex);
}
private void exchangeNumbers(int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
public static void main(String a[]){
MyQuickSort sorter = new MyQuickSort();
int[] input = {24,2,45,20,56,75,2,56,99,53,12};
sorter.sort(input);
for(int i:input){
System.out.print(i);
System.out.print(" ");
}
}
}5、归并排序
- 原理图
- 理解
将待排序的数列分成若干个长度为1的子数列,然后将这些数列两两合并;得到若干个长度为2的有序数列,再将这些数列两两合并;得到若干个长度为4的有序数列,再将它们两两合并;直接合并成一个数列为止。
- Java Code
public class MergeSort {
private int[] array;
private int[] tempMergArr;
private int length;
public static void main(String a[]){
int[] inputArr = {45,23,11,89,77,98,4,28,65,43};
MyMergeSort mms = new MyMergeSort();
mms.sort(inputArr);
for(int i:inputArr){
System.out.print(i);
System.out.print(" ");
}
}
public void sort(int inputArr[]) {
this.array = inputArr;
this.length = inputArr.length;
this.tempMergArr = new int[length];
doMergeSort(0, length - 1);
}
private void doMergeSort(int lowerIndex, int higherIndex) {
if (lowerIndex < higherIndex) {
int middle = lowerIndex + (higherIndex - lowerIndex) / 2;
// Below step sorts the left side of the array
doMergeSort(lowerIndex, middle);
// Below step sorts the right side of the array
doMergeSort(middle + 1, higherIndex);
// Now merge both sides
mergeParts(lowerIndex, middle, higherIndex);
}
}
private void mergeParts(int lowerIndex, int middle, int higherIndex) {
for (int i = lowerIndex; i <= higherIndex; i++) {
tempMergArr[i] = array[i];
}
int i = lowerIndex;
int j = middle + 1;
int k = lowerIndex;
while (i <= middle && j <= higherIndex) {
if (tempMergArr[i] <= tempMergArr[j]) {
array[k] = tempMergArr[i];
i++;
} else {
array[k] = tempMergArr[j];
j++;
}
k++;
}
while (i <= middle) {
array[k] = tempMergArr[i];
k++;
i++;
}
}
}常见排序算法复杂度
原文链接
本文为云栖社区原创内容,未经允许不得转载。