(1)单层感知机
1. 概念介绍:
假设输入空间(特征空间)是 ![]() ,输入空间是
,输入空间是![]()
![]() Y={+1,-1}. 输入
Y={+1,-1}. 输入![]() 表示实例的特征向量,对于应于输入空间(特征空间)的点;输出
表示实例的特征向量,对于应于输入空间(特征空间)的点;输出![]() 表示实例的类别.由输入空间到输出空间的如下函数:
表示实例的类别.由输入空间到输出空间的如下函数:
![]()
称为感知机。其中,w和b为感知机模型参数,![]() 叫做权值或者权值向量,
叫做权值或者权值向量,![]() 叫做偏置,
叫做偏置,![]() 表示w和x的内积,sign是符合函数,即
表示w和x的内积,sign是符合函数,即
感知机一种线性分类模型,属于判别模型。
单层感知机形象化理解:
感知机的几何解释:线性方程
![]()
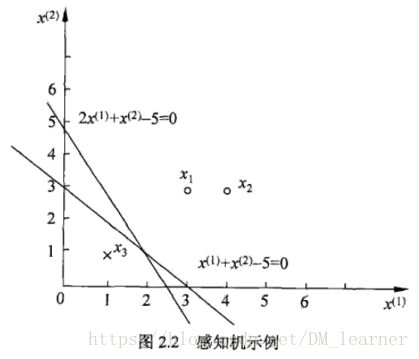
对应于特征空间的![]() 中的一个超平面S,其中w是超平面的法向量,b是超平面的截距,这个超平面将特殊空间划分为两部分,位于两部分的点(特征向量)分别被分为正、负两类。因此,超平面S成为分离超平面,如图所示:
中的一个超平面S,其中w是超平面的法向量,b是超平面的截距,这个超平面将特殊空间划分为两部分,位于两部分的点(特征向量)分别被分为正、负两类。因此,超平面S成为分离超平面,如图所示:
2. 感知机的学习策略
2.1关于数据集的线性可分性
定义(数据集的线性可分性)给定一个数据集 ![]() ,其中
,其中![]() ,
,![]() ,如果存在某个超平面S能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧,即对于所有的
,如果存在某个超平面S能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧,即对于所有的![]() 的实例i,都有
的实例i,都有![]() ,对所有的
,对所有的![]() 的实例i,有
的实例i,有![]() ,则称数据集T线性可分数据集,否则,称数据集T线性不可分。
,则称数据集T线性可分数据集,否则,称数据集T线性不可分。
2.2感知机的学习策略
假设训练数据集是线性可分的,感知机学习目标的要求是求得一个能够将训练集正实例点和负实例点完全分开的分离超平面。为了找到这样的超平面,需要知道感知机模型参数w和b,需要确定一个学习策略,即定义经验损失函数(![]() )并将损失函数极小化。
)并将损失函数极小化。
损失函数的一个自然选择是误分类点的总数,但是,这样的损失函数不是参数w和b的连续损失函数,不易优化。我们需要转变思路,可以使用误分类点到超平面的总距离来计算损失函数。思路如下:
首先写入输入空间![]() 中任一点
中任一点![]() 到超平面的距离:
到超平面的距离:
这里,![]() 是w的
是w的![]() 的范数。
的范数。
对于正确分类的点满足![]() ,而对于那些误分类的数据
,而对于那些误分类的数据![]() 来说,满足
来说,满足![]() ,因为误分类点线性不可能,那么误分类点
,因为误分类点线性不可能,那么误分类点![]() 到超平面S的距离为:
到超平面S的距离为:
这样,假设超平面S的误分类点的集合为M,那么所有的误分类点到超平面S的总距离为
不考虑![]() ,就得到感知机学习的损失函数。
,就得到感知机学习的损失函数。
给定训练数据集
![]()
其中,![]() ,
,![]() ,感知机
,感知机![]() 学习的损失函数定义为
学习的损失函数定义为
其中M为误分类点的集合,这个损失函数就是感知机学习的经验风险函数。
![]() 损失函数
损失函数![]() 是非负的,如果没有误分类点,损失函数值是0,而且,误分类点越少,误分类点离超平面的就越近,损失函数值就越小。一个特定的样本点的损失函数:在误分类时是参数为w,b的线性函数,在正确分类时0,因此,给定训练数据集T,损失函数
是非负的,如果没有误分类点,损失函数值是0,而且,误分类点越少,误分类点离超平面的就越近,损失函数值就越小。一个特定的样本点的损失函数:在误分类时是参数为w,b的线性函数,在正确分类时0,因此,给定训练数据集T,损失函数![]() 是w,b的连续可导函数。
是w,b的连续可导函数。
![]() 感知机学习的策略就是在假设空间中选取损失函数式最小的模型参数w,b,即感知机模型。
感知机学习的策略就是在假设空间中选取损失函数式最小的模型参数w,b,即感知机模型。
2.3 感知机学习算法
2.3.1 感知机学习算法的原始形式
感知机学习算法是对以下最优化问题的算法,给定一个训练数据集
![]()
其中,![]() ,
,![]() ,求参数w和b,使其为以下损失函数极小化问题的解
,求参数w和b,使其为以下损失函数极小化问题的解
其中M为误分类点的集合
感知机学习算法是误分类点驱动的,具体采用随机梯度下降算法。首先,任意选取一个超平面![]() ,然后用梯度下降算法不断地极小化目标函数(2.5)。极小化过程不是一次使得M中所有误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下架。
,然后用梯度下降算法不断地极小化目标函数(2.5)。极小化过程不是一次使得M中所有误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下架。
假设误分类点集合M是固定的,那么损失函数![]() 的梯度由
的梯度由
给出。
随机选取一个误分类点![]() ,对w,b进行更新:
,对w,b进行更新:
![]()
![]()
式中![]() 是步长,在统计学习中又称为学习率,这样通过迭代可以期待损失函数
是步长,在统计学习中又称为学习率,这样通过迭代可以期待损失函数![]() 不断减小,直到为0.综上所述,可以得到如下算法:
不断减小,直到为0.综上所述,可以得到如下算法:
感知机学习算法的原始形式
输入:训练数据集![]() ,其中
,其中![]() ,
,![]() ;学习率
;学习率![]() ;
;
输出:w,b;感知机模型![]()
(1)选取初值![]()
(2)在训练集中选取数据![]()
(3)如果![]()
![]()
![]()
(4)转至(2),直至训练集中没有误分类点。
例1.如图所示的训练数据集,其正实例点是![]() 负实例点是
负实例点是![]() ,试用感知机学习算法的原始形式求感知机模型
,试用感知机学习算法的原始形式求感知机模型![]() .这里,
.这里,![]()
解构建最优化问题:
按照感知机学习算法的原始形式,求解w,b。这里![]() .
.
(1)去初值![]()
(2)对![]() ,
,![]() ,未能被正确分类,更新w,b
,未能被正确分类,更新w,b
![]()
得到线性模型
![]()
(3)对于![]() 显然,
显然,![]() ,被正确分类,不修改w,b;
,被正确分类,不修改w,b;
对![]() ,
,![]() ,被误分类,更新w,b.
,被误分类,更新w,b.
![]()
得到线性模型
![]()
如此继续下去,直到
![]()
![]() 线性模型:
线性模型: ![]()
![]() 对于所有的数据点
对于所有的数据点![]() ,即没有误分类点,损失函数达到极小。
,即没有误分类点,损失函数达到极小。
分离超平面为 ![]()
感知机模型为 ![]()
代码如下:
#!usr/bin/env python3
#coding=utf-8
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
"感知机的原始形式"
x=np.array([[3,3],[4,3],[1,1]]) #建立数据集,共是三个实例
y=np.array([1,1,-1]) #创建标签
store=[]
w=np.array([0, 0])
b=0 #初始化参数w,b
k=0 #k计算迭代次数
learnrate=1 #设置学习率为1
condition=True
while condition:
count=0
for i in range(len(x)):
if y[i]*(np.dot(w,x[i].T)+b)<=0: #用来检测误分类
w=w+learnrate*y[i]*x[i].T #更新w
b=b+learnrate*y[i] #更新b
store.append([w,b])
count=count+1
k=k+1
print('w的值:{0} b的值:{1} 迭代次数:{2}'.format(w, b, k))
if count==0:
k=k+1
print('w的值:{0} b的值:{1} 迭代次数:{2}'.format(w, b, k))
store.append([w,b])
condition=False
print(store)
fig=plt.figure()
ax=plt.axes(xlim=(-7,7),ylim=(-7,7))
line,=ax.plot([],[],'b',linewidth=3)
label=ax.text([],[],'')
#用来画出是三个实例点
def plot_three_point():
global x, y, line, label
plt.axis([-6,6,-6,6])
p1=plt.scatter(x[0:2,0],x[0:2,1],c='b',marker='o',s=60)
p2=plt.scatter(x[2,0],x[2,1],c='r',marker='x',s=60)
plt.grid(True)
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend([p1,p2],['正实例点','负实例点'],loc=1)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.title('感知机迭代过程图')
return line,label
#画出动态的图形
def animate(index):
global store,ax,line,label
w=store[index][0]
b=store[index][1]
if w[1]==0:
return line,label
x1=-6
y1=-(b+w[0]*x1)/w[1]
x2=6
y2=-(b+w[0]*x2)/w[1]
line.set_data([x1,x2],[y1,y2])
x1=0
y1=-(b+w[0]*x1)/w[1]
label.set_text("w:{}".format(str(store[index][0])) + ' ' +"b:{}".format(str(b)))
label.set_position([x1,y1])
return line,label
ani=animation.FuncAnimation(fig,animate,init_func=plot_three_point,frames=len(store),interval=1000,repeat=True,blit=True)
plt.show()
ani.save('perceptron.gif',fps=200,writer='imagemagick')
2.3.2 算法的收敛性
关于线性可分数据集感知机学习算法原始形式收敛问题,我们可以转换为即通过有限次迭代可以得到一个将训练数据集完全正确划分的分离超平面及感知机模型。
为了便于推导,在这里我们将偏置b并入权重向量w,记作![]() ,同样也将输入向量加以扩充,加进常数1,记作
,同样也将输入向量加以扩充,加进常数1,记作![]() 。这样,
。这样,![]() 。显然,
。显然, ![]()
- 定理:设训练数据集
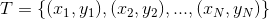 是线性可分的,其中
是线性可分的,其中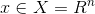 ,
,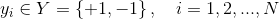 ,则有
,则有
(1)存在满足条件![]() 的超平面
的超平面![]() 将训练数据集完全正确分开;且存在
将训练数据集完全正确分开;且存在![]() ,对所有
,对所有![]() 则有
则有
![]()
(2)令 ![]() ,感知机学习算法的原始形式在误分类次数k满足不等式
,感知机学习算法的原始形式在误分类次数k满足不等式
证明如下图所示:
证明(1)
证明(2)
2.3.3 感知机学习算法的对偶形式
对偶形式的基本思想:将w和b表示为实例![]() 和标记
和标记![]() 的线性组合形式,通过求解其系数而求得w和b。不失一般性,在感知机学习算法的原始形式中,可初始化
的线性组合形式,通过求解其系数而求得w和b。不失一般性,在感知机学习算法的原始形式中,可初始化![]() 均为0,对于误分类点
均为0,对于误分类点![]() 通过
通过
![]()
![]()
逐步修改w,b,设修改n次,则w,b关于![]() 的增量分别是
的增量分别是![]() 和
和![]() ,这里
,这里![]() 。这样,从学习过程不难看出,最后学习到的w,b可以分别表示为
。这样,从学习过程不难看出,最后学习到的w,b可以分别表示为
这里,![]() ,当
,当![]() 时,表示第i个实例点由于误分而进行更新的次数。实例点更新次数越多,意味着它距离分离超平面越近,也就越难正确分类。换句话说,这样的实例对学习结果影响最大。
时,表示第i个实例点由于误分而进行更新的次数。实例点更新次数越多,意味着它距离分离超平面越近,也就越难正确分类。换句话说,这样的实例对学习结果影响最大。
感知机学习算法的对偶形式
输入:线性可分的数据集![]() ,其中
,其中![]() ,
,![]() ;学习率
;学习率![]() ;
;
其中,![]() .
.
(1)![]()
(2)在训练集中选取数据![]()
![]()
![]()
(4)转至(2)直到没有误分类数据
对偶形式中训练实例仅以内积的形式出现,为了方便,可以预先将训练集中的实例间的内积计算出来并以矩阵的形式存储,这个矩阵就是所谓的Gram矩阵
![]()
例2.数据同例1,正样本点是![]() ,
,![]() ,负样本点是
,负样本点是![]() ,试用感知机学习算法对偶形式求感知机模型。
,试用感知机学习算法对偶形式求感知机模型。
解 按照感知机算法对偶形式求感知机模型
(1)取![]()
(2)计算Gram矩阵
(3)误分条件
参数更新
![]()
(4)经过多次迭代和更新![]() 值可以得到最终结果
值可以得到最终结果
![]()
![]()
分离超平面
![]()
最终得到感知机模型
![]()
运行的代码如下所示:
#!usr/bin/env python3
#coding=utf-8
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation"感知机的对偶形式"
x=np.array([[3,3],[4,3],[1,1]]) #建立数据集,共是三个实例
y=np.array([1,1,-1]) #创建标签
list_1=[] #用于存储w,b参数
list=[] #用于存储变化的alpha,b值gramMatrix=x.dot(x.T)
alpha=np.zeros(len(x))
b=0 #参数b初始化
k=0 #k计算迭代次数
learnrate=1 #设置学习率为1
condition=True
while condition:
count=0
for i in range(len(x)):
if y[i]*(np.sum(alpha*y*gramMatrix[i])+b)<=0:
alpha[i]=alpha[i]+learnrate
b=b+learnrate*y[i]
list_1.append([(alpha*y.T).dot(x),b])
list.append([np.array(alpha),b])
print(alpha)
k=k+1
count=count+1
print('alpha:{0} b:{1} k:{2}'.format(alpha, b, k))
if count==0:
condition=False
#print(list_1)
#print(list)fig=plt.figure()
ax=plt.axes(xlim=(-7,7),ylim=(-7,7))
line,=ax.plot([],[],'b',linewidth=3)
label=ax.text([],[],'')#用来画出是三个实例点
def plot_three_point():
global x, y, line, label
plt.axis([-6,6,-6,6])
p1=plt.scatter(x[0:2,0],x[0:2,1],c='b',marker='o',s=60)
p2=plt.scatter(x[2,0],x[2,1],c='r',marker='x',s=60)
plt.grid(True)
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend([p1,p2],['正实例点','负实例点'],loc=1)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.title('感知机对偶形式迭代过程图')
return line,label#画出动态的图形
def animate(index):
global list_1,ax,line,label
w=list_1[index][0]
b=list_1[index][1]
if w[1]==0:
return line,label
x1=-6
y1=-(b+w[0]*x1)/w[1]
x2=6
y2=-(b+w[0]*x2)/w[1]
line.set_data([x1,x2],[y1,y2])
x1=0
y1=-(b+w[0]*x1)/w[1]
label.set_text("alpha:{}".format(str(list[index][0])) + ' ' +"b:{}".format(str(b)))
label.set_position([x1,y1])
return line,label
ani=animation.FuncAnimation(fig,animate,init_func=plot_three_point,frames=len(list_1),interval=1000,repeat=True,blit=True)
plt.show()
ani.save('perceptron_dual_form.gif',fps=200,writer='imagemagick')




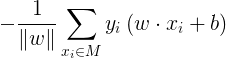

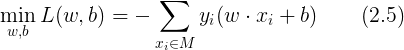




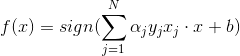
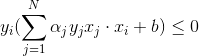
![G=\left[ \begin{matrix} 18 & 21 & 6 \\ 21 & 25 & 7 \\ 6 & 7 & 2 \end{matrix} \right]](http://img.e-com-net.com/image/info8/9c340cad5cb04cf58cc6effa821fe50d.gif)