时间卷积网络(TCN):结构+pytorch代码
文章目录
- TCN
- TCN结构
- 1-D FCN的结构
- 因果卷积(Causal Convolutions)
- 膨胀因果卷积(Dilated Causal Convolutions)
- 膨胀非因果卷积(Dilated Non-Causal Convolutions)
- 残差块结构
- pytorch代码讲解
TCN
TCN(Temporal Convolutional Network)是由Shaojie Bai et al.提出的,paper地址:https://arxiv.org/pdf/1803.01271.pdf
想要了解TCN,最好先知道CNN和RNN。
以往一旦提起sequence,或者存在时间序列的数据,想到的神经网络模型就是RNN及其变种LSTM、GRU等。在上面论文提到,很多工作表明,在RNN这个框架中,很难再找到新的模型,其效果可以在很多任务中超越LSTM,但是跳出RNN这个框架,paper作者展示了利用CNN衍生出的TCN结构就很容易在很多任务中取得超过LSTM、GRU的效果。当然paper作者也表示,TCN并不指代一种模型,更像是一种类似RNN的框架,paper作者渴望抛砖引玉,让更多人来探索挖掘这个框架的能力。
TCN结构
TCN的设计十分巧妙,同ConvLSTM不同的是,ConvLSTM通过引入卷积操作,让LSTM网络可以处理图像信息,其卷积只对一个时间的输入图像进行操作,TCN则直接利用卷积强大的特性,跨时间步提取特征。
TCN结构很像Wavenet,paper作者也表示确实借鉴了Wavenet的结构,TCN的结构在paper中表示如下,这是一个 k e r n e l s i z e = 3 , d i l a t i o n s = [ 1 , 2 , 4 ] kernel~size = 3, dilations = [1, 2, 4] kernel size=3,dilations=[1,2,4]的TCN。
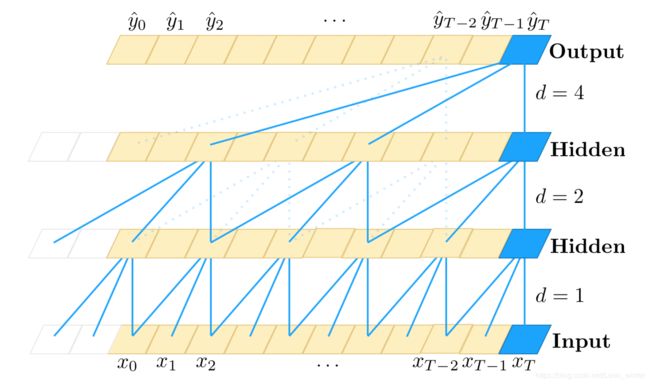
下图展示了更直接的TCN结构, k e r n e l s i z e = 2 , d i l a t i o n s = [ 1 , 2 , 4 , 8 ] kernel~size = 2, dilations = [1, 2, 4, 8] kernel size=2,dilations=[1,2,4,8]
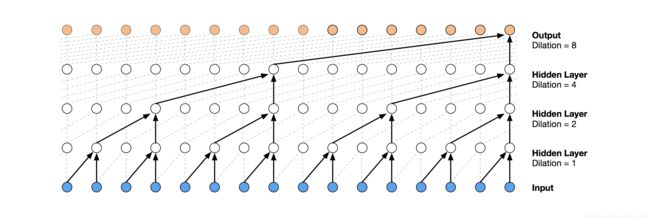
kernel size等于2,即每一层的输入,是上一层的两个时刻的输出;dilations = [1, 2, 4, 8],即每一层的输入的时间间隔有多大,dilation=4,即上一层每前推4个时间步的输出,作为这一层的输入,直到取够kernal size个输入。
TCN要实现RNN的类似功能,需要解决两个问题,
- TCN如何像RNN那样,输入多长的时间步,输出时间步也是同样长度,或者说,每个时间的输入都有对应的输出;
- 如何保证历史数据不漏接(no leakage)。
为了解决上面的两个问题,paper作者分别引入了1-D FCN和因果卷积(Causal Convolutions),可以说
T C N = 1 D F C N + C a u s a l C o n v o l u t i o n s TCN = 1D~FCN + Causal~Convolutions TCN=1D FCN+Causal Convolutions
1-D FCN的结构
为了解决第一个问题,TCN利用了1-D FCN的结构,每一个隐层的输入输出的时间长度都相同,维持相同的时间步,具体来看,第一隐层不管kernel size和dilation为多少,输入若是n个时间步,输出也是n个时间步,同样第二隐层,第三隐层。。。的输入输出时间步长度都是n,这点和RNN就很像,不管在哪一层,每个时间步的输入都会有对应的输出。
对于第一个时间步,没有任何历史的信息,TCN认为其历史数据全是0 (其实就是卷积操作的padding,这一点最好结合下面的代码理解),同时paper作者通过实验发现,TCN保留长远历史信息的能力较LSTM更强。
因果卷积(Causal Convolutions)
为了解决第二个问题,TCN利用因果卷积(Causal Convolutions),所谓因果,也就是对于输出t时刻的数据 y t y_{t} yt,其输入只可能是t以及t以前的时刻,即 x 0 … x t x_{0}\dots x_{t} x0…xt,其结构如下:

不难发现,这样的卷积连接好像和最上面的TCN结构图不太一样,理论上利用因果卷积是可以搭建TCN,但是如果我们的输出和之前的1000个时间点都存在联系,要获取这种联系,因果卷积构成的TCN深度就是1000-1,如果和历史的10000个时间点有联系,那么深度就是10000-1…,那样TCN就太深了。
膨胀因果卷积(Dilated Causal Convolutions)
为了有效的应对长历史信息这一问题,paper作者利用了膨胀因果卷积(Dilated Causal Convolutions),还是具有因果性,只不过引入了膨胀因子(dilation factor) d d d,对于 k e r n e l s i z e = 2 , d i l a t i o n s = [ 1 , 2 , 4 , 8 ] kernel~size = 2, dilations = [1, 2, 4, 8] kernel size=2,dilations=[1,2,4,8]的TCN,其结构如下:

一般膨胀系数是2的指数次方,即1,2,4,8,16,32…
膨胀非因果卷积(Dilated Non-Causal Convolutions)
LSTM是可以双边输入的,输入不仅利用历史信息,也利用了未来信息,TCN也能做到类似的实现,利用膨胀非因果卷积(Dilated Non-Causal Convolutions),下图展示了 k e r n e l s i z e = 3 , d i l a t i o n s = [ 1 , 2 , 4 , 8 ] kernel~size = 3, dilations = [1, 2, 4, 8] kernel size=3,dilations=[1,2,4,8]的膨胀非因果卷积构成的TCN:
残差块结构
同时,就算我们使用了膨胀因果卷积,有时模型可能仍然很深,较深的网络结构可能会引起梯度消失等问题,为了应对这种情况,paper作者利用了一种类似于ResNet中的残差块的结构,这样设计的TCN结构更加的具有泛化能力(generic)。
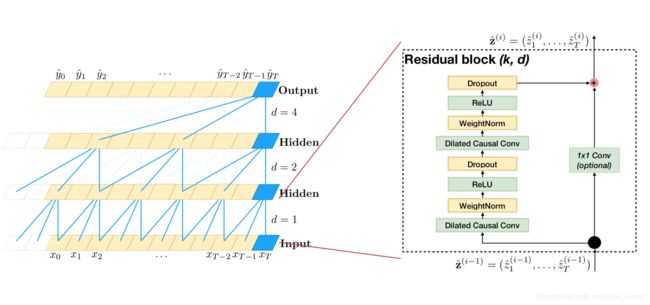
o = A c t i v a t i o n ( x + F ( x ) ) o=Activation(x+F(x)) o=Activation(x+F(x))
可以看出来,残差结构替代了TCN层与层之间的简单连接,由于 x x x和 F ( x ) F(x) F(x)之间的通道数可能不一样,所以这里设计了一个 1 × 1 C o n v 1\times1~Conv 1×1 Conv来对x做一个简单的变换,使得变换后的 x x x与 F ( x ) F(x) F(x)可以相加。其实这里的图都有一定的欺骗性,每一层每个时刻只有一个网格并不代表这一时刻的通道数等于1。
pytorch代码讲解
paper给的代码是pytorch版本的,获取点这里,其中TCN模型部分的代码如下,重难点部分给出了注释。
import torch
import torch.nn as nn
from torch.nn.utils import weight_norm
class Chomp1d(nn.Module):
def __init__(self, chomp_size):
super(Chomp1d, self).__init__()
self.chomp_size = chomp_size
def forward(self, x):
"""
其实这就是一个裁剪的模块,裁剪多出来的padding
"""
return x[:, :, :-self.chomp_size].contiguous()
class TemporalBlock(nn.Module):
def __init__(self, n_inputs, n_outputs, kernel_size, stride, dilation, padding, dropout=0.2):
"""
相当于一个Residual block
:param n_inputs: int, 输入通道数
:param n_outputs: int, 输出通道数
:param kernel_size: int, 卷积核尺寸
:param stride: int, 步长,一般为1
:param dilation: int, 膨胀系数
:param padding: int, 填充系数
:param dropout: float, dropout比率
"""
super(TemporalBlock, self).__init__()
self.conv1 = weight_norm(nn.Conv1d(n_inputs, n_outputs, kernel_size,
stride=stride, padding=padding, dilation=dilation))
# 经过conv1,输出的size其实是(Batch, input_channel, seq_len + padding)
self.chomp1 = Chomp1d(padding) # 裁剪掉多出来的padding部分,维持输出时间步为seq_len
self.relu1 = nn.ReLU()
self.dropout1 = nn.Dropout(dropout)
self.conv2 = weight_norm(nn.Conv1d(n_outputs, n_outputs, kernel_size,
stride=stride, padding=padding, dilation=dilation))
self.chomp2 = Chomp1d(padding) # 裁剪掉多出来的padding部分,维持输出时间步为seq_len
self.relu2 = nn.ReLU()
self.dropout2 = nn.Dropout(dropout)
self.net = nn.Sequential(self.conv1, self.chomp1, self.relu1, self.dropout1,
self.conv2, self.chomp2, self.relu2, self.dropout2)
self.downsample = nn.Conv1d(n_inputs, n_outputs, 1) if n_inputs != n_outputs else None
self.relu = nn.ReLU()
self.init_weights()
def init_weights(self):
"""
参数初始化
:return:
"""
self.conv1.weight.data.normal_(0, 0.01)
self.conv2.weight.data.normal_(0, 0.01)
if self.downsample is not None:
self.downsample.weight.data.normal_(0, 0.01)
def forward(self, x):
"""
:param x: size of (Batch, input_channel, seq_len)
:return:
"""
out = self.net(x)
res = x if self.downsample is None else self.downsample(x)
return self.relu(out + res)
class TemporalConvNet(nn.Module):
def __init__(self, num_inputs, num_channels, kernel_size=2, dropout=0.2):
"""
TCN,目前paper给出的TCN结构很好的支持每个时刻为一个数的情况,即sequence结构,
对于每个时刻为一个向量这种一维结构,勉强可以把向量拆成若干该时刻的输入通道,
对于每个时刻为一个矩阵或更高维图像的情况,就不太好办。
:param num_inputs: int, 输入通道数
:param num_channels: list,每层的hidden_channel数,例如[25,25,25,25]表示有4个隐层,每层hidden_channel数为25
:param kernel_size: int, 卷积核尺寸
:param dropout: float, drop_out比率
"""
super(TemporalConvNet, self).__init__()
layers = []
num_levels = len(num_channels)
for i in range(num_levels):
dilation_size = 2 ** i # 膨胀系数:1,2,4,8……
in_channels = num_inputs if i == 0 else num_channels[i-1] # 确定每一层的输入通道数
out_channels = num_channels[i] # 确定每一层的输出通道数
layers += [TemporalBlock(in_channels, out_channels, kernel_size, stride=1, dilation=dilation_size,
padding=(kernel_size-1) * dilation_size, dropout=dropout)]
self.network = nn.Sequential(*layers)
def forward(self, x):
"""
输入x的结构不同于RNN,一般RNN的size为(Batch, seq_len, channels)或者(seq_len, Batch, channels),
这里把seq_len放在channels后面,把所有时间步的数据拼起来,当做Conv1d的输入尺寸,实现卷积跨时间步的操作,
很巧妙的设计。
:param x: size of (Batch, input_channel, seq_len)
:return: size of (Batch, output_channel, seq_len)
"""
return self.network(x)
参考资料:
TCN: https://arxiv.org/pdf/1803.01271.pdf
因果卷积(causal)与扩展卷积(dilated):https://blog.csdn.net/tonygsw/article/details/81280364
philipperemy/keras-tcn
:https://github.com/philipperemy/keras-tcn#why-temporal-convolutional-network