感知机模型-原始版本【python实现】

概览

感知机(perceptron)是一个二分类模型。对于输入的特征向量，会输出两个类别（1和-1）。
perceptron是一个判别模型。（在1957年提出。）

数学模型

f(x)=sign(w⋅x+b) f ( x ) = s i g n ( w · x + b )

• x x 为输出
• w w 为权重
• b b 为偏置（bias）
• sign s i g n 是符号函数

学习策略

• 定义： 数据集的线性可分性。给定一个数据集合，当能找到一个 w∗x+1=0 w ∗ x + 1 = 0 超平面，将整个数据集完全划分。

感知机采用的是，任何一个点到超平面的距离。

|w⋅x+b|∥w∥ | w · x + b | ‖ w ‖

• 分母处为二范数

考虑误判的点

• (yi,xi) ( y i , x i ) ：误判就是该是正的适合变成负的，该是负的时候变成正的了
  
  • yi>0 y i > 0 & w⋅xi+b<0 w · x i + b < 0
  • yi<0 y i < 0 & w⋅xi+b>0 w · x i + b > 0

整理一下，就是

yi∗(w⋅xi+b)<0 y i ∗ ( w · x i + b ) < 0

对于所有的误判求个和，那就是要保证下面这个函数最小。

L(w,b)=−∑xi∈Myi∗(w⋅xi+b) L ( w , b ) = − ∑ x i ∈ M y i ∗ ( w · x i + b )

M M 为误差分类的集合。
误差函数特性;

• 非负
• 连续可导（在正确地方为0，原因是这个点没有被求和啊；在误差的点上关于w,b是一个线性函数（只是求和了而已），自然连续可导）

通过矩阵求导（在矩阵论会学到，但是提前的话，直接用普通函数式子的求导，算出来的结果是一样的。）

得到w的梯度和b的梯度。

感知机的原始形式

在所有点集中，选点 (xi,yi) ( x i , y i ) ，如果 yi(w⋅xi+b)≤0 y i ( w · x i + b ) ≤ 0 （有误差），那就用 w+yi∗xi w + y i ∗ x i 来代替原来的w。同样，用 b+yi b + y i 代替原来的b。

当然，一般来说会对所加梯度上，乘上一个系数，作为学习系数。（即，顺着改变的动力）。

这个算法会一直进行，直到最后没有误差就end。

代码

import numpy as np
import matplotlib.pyplot as plt


def draw(w, b, label='before'):
    fontsize = 15
    plt.figure(1, figsize=(8, 6))
    plt.clf()  # clear current figure
    plt.title(label)
    plt.scatter(data[:, 0], data[:, 1], c=target, cmap=plt.cm.Set1, edgecolors='k')
    plt.xlabel('Sepal length', fontsize=fontsize)
    plt.ylabel('Sepal width', fontsize=fontsize)
    plt.xlim(x_min, x_max)
    plt.ylim(y_min, y_max)
    ys = list(map(lambda x: (-w[0] * x + b) / w[1], [x_min, x_max]))
    plt.plot([x_min, x_max], ys)
    plt.show()


if __name__ == '__main__':
    data = np.array([[-1, 1], [1, 3], [0, -2]])
    target = [-1, 1, -1]
    shape = data.shape
    # random initial
    np.random.seed(5)

    w = np.random.random(shape[-1])
    b = np.random.random()

    x_min, x_max = data[:, 0].min() - 0.5, data[:, 0].max() + 0.5
    y_min, y_max = data[:, 1].min() - 0.5, data[:, 1].max() + 0.5
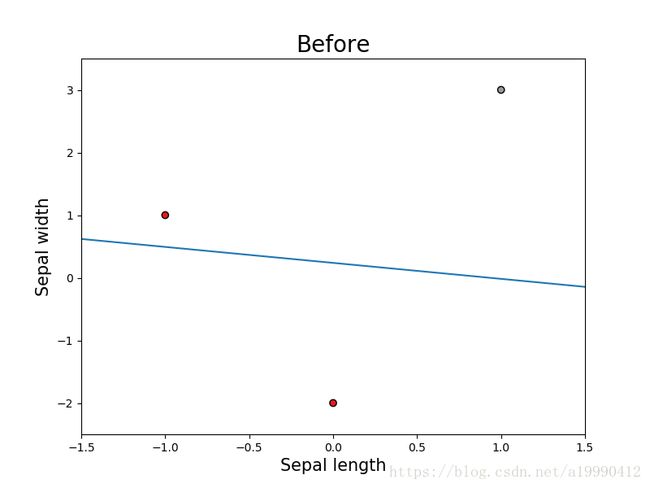
    draw(w, b)

    lamb = 0.5
    MAX_TIME = 1000
    for t in range(MAX_TIME):
        change = False
        for i in range(shape[0]):
            if target[i] * (np.dot(w, data[i]) + b) <= 0:
                w += lamb * target[i] * data[i]
                b += lamb * target[i]
                change = True
        if not change:
            break

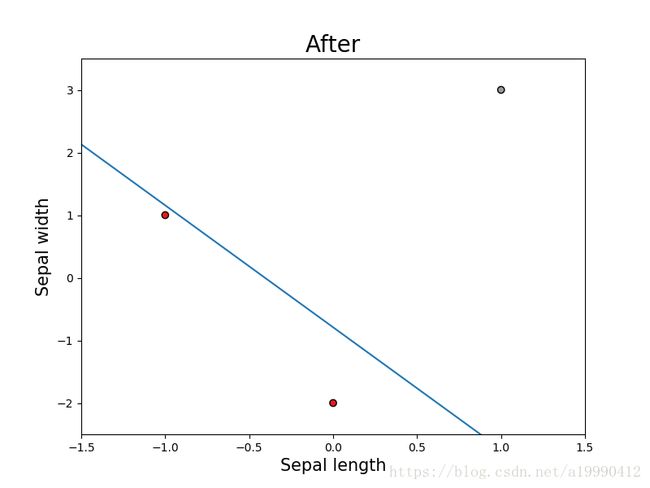
    draw(w, b, 'after')