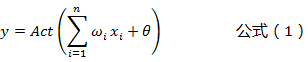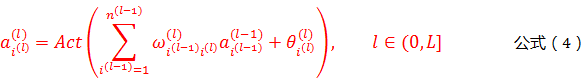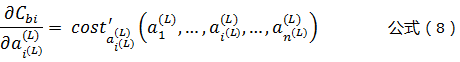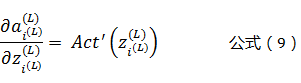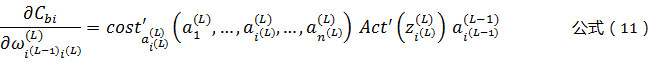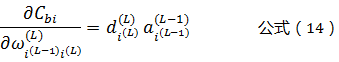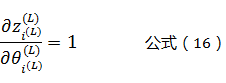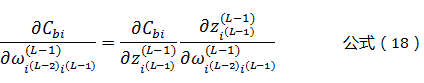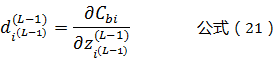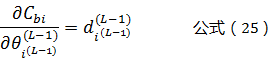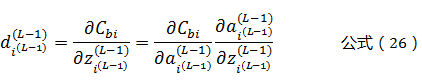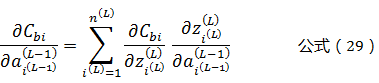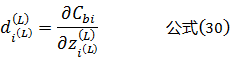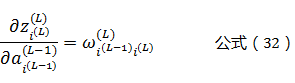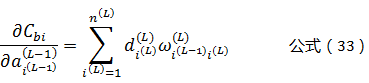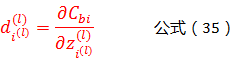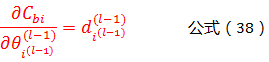【神经网络算法入门】详细推导全连接神经网络算法及反向传播算法+Python实现代码

一、单个神经元

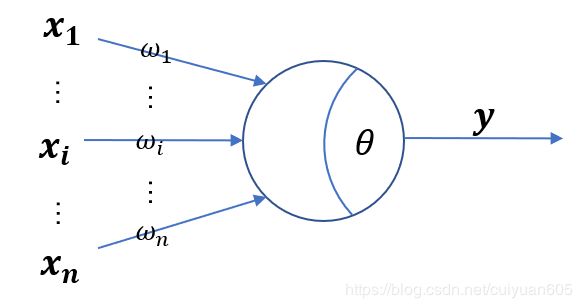
神经网络算法，是使用计算机模拟生物神经系统，来模拟人类思维方式的算法。它的基本单位就是人工神经元。通过相互连接形成一张神经网络。

生物神经网络中，每个神经元与其他神经元连接，当它“激活”时，会传递化学物质到相连的神经元，改变其他神经元的电位，当电位达到一定“阈值”，那么这个神经元也会被激活。

单个人工神经元的计算公式：

其中：

 为输入参数向量，表示其他神经元输入的信号。

 为每个输入参数的权重值，表示对应神经元信号的权重。

θ为阈值或者偏差值，是指该激活神经元的难易程度。

y为神经元的输出值，表示该神经元是否被激活。

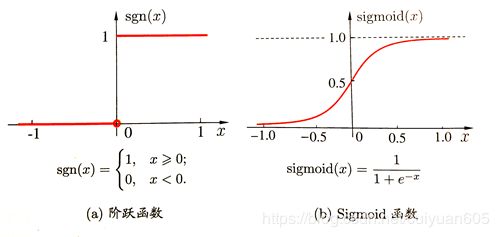
Act()为激活函数，理想的激活函数是下图（a）中的跃阶函数，“1”为神经元兴奋，“0”为神经元抑制，但由于跃阶函数具有不是连续可导等不好的性质，因此一般采用下图（b）的Sigmoid函数作为激活函数。

 

二、全连接神经网络结构

我们来定义一个全连接神经网络：

全连接神经网络，就是指每一层的每个神经元都和下一层的每个神经元相连接。

Layer：0为输入层，

Layer：L为输出层

其他L-1个Layer为隐层

输入x

 

我们称一个输入值x为一个样本

输出 y

变量的上标（0）（L），表示该变量处于神经网络的哪一层。

表示第L层编号为i的神经元。 表示第L层的神经元数量。

更好的理解神经网络，可观看此视频：https://www.bilibili.com/video/av15532370

 

三、反向传播算法（BP算法）

下面来说明如何调整一个神经网络的参数，也就是误差反向传播算法（BP算法）。以得到一个能够根据输入，预测正确输出的模型。

1、首先我们要了解优化的目标

根据人工神经元的定义，有以下三个公式：

其中，Act()是激活函数，之前已经说过。

根据公式(2)和公式(3)，可以得出各个神经元之间的通用计算公式，如下所示：

公式(4)是人工神经网络正向传播的核心公式。

 

那么，我们根据什么来调整神经网络的参数，以得到一个能够正确预测结果的模型呢？请看下面的公式：

公式(5)用来计算我们期望的输出和实际输出的“差别”，其中cost()叫做损失函数。我们的期望是损失值达到最小。

但是，只根据一次输出的损失值，对参数进行调整，无法使模型适应所有输入样本。我们需要的是，调整参数，使得所有输入样本，得到输出的总损失值最小，而不是只让其中一个样本的损失值最小，导致其他样本损失值增大。因此有如下公式：

公式(6)表示一个batch的所有样本输出的总损失值的平均值。其中，bn表示一个batch中样本的数量。

为什么不用所有的样本计算损失值，而将所有样本分成一个个的batch呢？因为所有的训练样本数量太大了，可能有数以百万计，将所有的样本损失值都一起进行运算，计算量过于庞大，大大降低了模型计算的速度。

公式(6)中计算总的损失值C，其实是一个以所有的连接权值ω和所有的阈值θ未为变量的多元函数。我们想要的模型就是求得C最小时，所有ω和θ的值。直接计算显然是不可能的，因为对于一个大的深度神经网络，所有的参数变量，可能数以万计。

在这里我们使用梯度下降算法来逐步逼近C的最小值，也就是先随机得到一组参数变量的值，然后计算参数变量当前的梯度，向梯度的反方向，也就是C变小最快的方向，逐步调整参数值，最终得到C的最小值，或者近似最小值。

而将所有样本，随机分成一个个固定长度的batch，以得到近似的梯度方向，叫做随机梯度下降算法。

更好理解梯度下降算法，逐步求得最优的参数值，可观看此视频：https://www.bilibili.com/video/av16144388

 

2、开始求梯度

那么，根据梯度的定义，接下来的任务，就是求取各个参数变量相对于C的偏导数。我们将使用误差反向传播算法来求取各个参数变量的偏导数。

这里先剧透一下，求取参数偏导数的方法，和神经网络正向传播（根据样本计算输出值）的方式类似，也是逐层求解，只是方向正好相反，从最后一层开始，逐层向前。

更好的理解误差反向传播算法，可观看此视频：https://www.bilibili.com/video/av16577449

首先，我们先求神经网络最后一层，也就是输出层的相关参数的偏导数。为了降低推导的复杂性，我们只计算相对于一个样本的损失值函数Cbi的偏导数，因为相对于总损失值函数C的偏导数值，也不过是把某个参数的所有相对于Cbi偏导数值加起来而已。

根据公式(2)、公式(3)、公式(5)，以及“复合函数求导法则”，可以得到输出层（L层）某个神经元的权值参数ω的偏导数，计算公式如下：

根据公式(5)可以得到：

根据公式(2)可以得到：

根据公式(3)可以得到：

将公式(8)(9)(10)，带入公式(7)，可以得到：

 

我们令：

根据公式(8)(9)则有：

将公式(13)，带入公式(11)，可以得到：

这样我们就得到了输出层L相关的权值参数ω的偏导数计算公式！

接下来，同理可得输出层L相关的阈值θ的偏导数计算公式为：

而根据公式(3)可以得到：

将公式(16)带入公式(15)可以得到：

这就是输出层L相关的阈值θ的偏导数计算公式！

 

3、根据L层，求前一层参数的偏导函数

由公式(3)可知，一个权值参数ω只影响一个L-1层的神经元，因此有：

根据公式(3)可以得到：

将公式(19)带入公式(18)可以得到：

根据公式(12)可以得到：

将公式(21)带入公式(20)可以得到：

同理，我们可以得到：

根据公式(3)可以得到：

将公式(24)带入公式(23)可以得到：

这样我们就得到了L-1层神经元相关参数的计算公式！

 

下面，我们还需要推导一下 之间的关系，根据公式(2)可以得到：

同样根据公式(2)可以得到：

将公式(27)带入公式(26)可以得到：

由公式(3)可知，一个权值参数ω只影响一个L-1层的神经元，但这个L-1层神经元影响了所有L层的神经元。因此，根据“多元复合函数求导法则”有：

根据公式(12)可以得到：

将公式(27)带入公式(26)可以得到：

根据公式(3)可以得到：

将公式(32)带入到公式(31)可以得到：

将公式(33)带入公式(28)可以得到：

这样我们就得到了反向传播，逐层推导的通用公式：

在这里，ω和z都是正向传播过程中，已经算好的常数，而  可以从L层开始逐层向前推导，直到第1层，第0层是输入层，不需要调整参数。而第L层的   可参考公式(13)。

 

下面是全连接神经网络的python实现代码：

#coding=utf-8
import numpy as np
import matplotlib.pylab as plt
import random

class NeuralNetwork(object):
    def __init__(self, sizes, act, act_derivative, cost_derivative):
        #sizes表示神经网络各层的神经元个数，第一层为输入层，最后一层为输出层
        #act为神经元的激活函数
        #act_derivative为激活函数的导数
        #cost_derivative为损失函数的导数
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.biases = [np.random.randn(nueron_num, 1) for nueron_num in sizes[1:]]
        self.weights = [np.random.randn(next_layer_nueron_num, nueron_num)
            for nueron_num, next_layer_nueron_num in zip(sizes[:-1], sizes[1:])]
        self.act=act
        self.act_derivative=act_derivative
        self.cost_derivative=cost_derivative

    #前向反馈（正向传播）
    def feedforward(self, a):
        #逐层计算神经元的激活值，公式(4)
        for b, w in zip(self.biases, self.weights):
            a = self.act(np.dot(w, a)+b)
        return a

    #随机梯度下降算法
    def SGD(self, training_data, epochs, batch_size, learning_rate):
        #将训练样本training_data随机分为若干个长度为batch_size的batch
        #使用各个batch的数据不断调整参数，学习率为learning_rate
        #迭代epochs次
        n = len(training_data)
        for j in range(epochs):
            random.shuffle(training_data)
            batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]
            for batch in batches:
                self.update_batch(batch, learning_rate)
            print("Epoch {0} complete".format(j))

    def update_batch(self, batch, learning_rate):
        #根据一个batch中的训练样本，调整各个参数值
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        #计算梯度，并调整各个参数值
        self.weights = [w-(learning_rate/len(batch))*nw for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(learning_rate/len(batch))*nb for b, nb in zip(self.biases, nabla_b)]

    #反向传播
    def backprop(self, x, y):
        #保存b和w的偏导数值
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        #正向传播
        activation = x
        #保存每一层神经元的激活值
        activations = [x]
        #保存每一层神经元的z值
        zs = []
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = self.act(z)
            activations.append(activation)
        #反向传播得到各个参数的偏导数值
        #公式(13)
        d = self.cost_derivative(activations[-1], y) * self.act_derivative(zs[-1])
        #公式(17)
        nabla_b[-1] = d
        #公式(14)
        nabla_w[-1] = np.dot(d, activations[-2].transpose())
        #反向逐层计算
        for l in range(2, self.num_layers):
            z = zs[-l]
            sp = self.act_derivative(z)
            #公式(36)，反向逐层求参数偏导
            d = np.dot(self.weights[-l+1].transpose(), d) * sp
            #公式(38)
            nabla_b[-l] = d
            #公式(37)
            nabla_w[-l] = np.dot(d, activations[-l-1].transpose())
        return (nabla_b, nabla_w)

#距离函数的偏导数
def distance_derivative(output_activations, y):
    #损失函数的偏导数
    return 2*(output_activations-y)

# sigmoid函数
def sigmoid(z):
    return 1.0/(1.0+np.exp(-z))

# sigmoid函数的导数
def sigmoid_derivative(z):
    return sigmoid(z)*(1-sigmoid(z))

if __name__ == "__main__":
    #创建一个5层的全连接神经网络，每层的神经元个数为1，8，5，3，1
    #其中第一层为输入层，最后一层为输出层
    network=NeuralNetwork([1,8,5,3,1],sigmoid,sigmoid_derivative,distance_derivative)

    #训练集样本
    x = np.array([np.linspace(-7, 7, 200)]).T
    #训练集结果，由于使用了sigmoid作为激活函数，需保证其结果落在(0,1)区间内
    y = (np.cos(x)+1)/2

    #使用随机梯度下降算法（SGD）对模型进行训练
    #迭代5000次；每次随机抽取40个样本作为一个batch；学习率设为0.1
    training_data=[(np.array([x_value]),np.array([y_value])) for x_value,y_value in zip(x,y)]
    network.SGD(training_data,5000,40,0.1)

    #测试集样本
    x_test = np.array([np.linspace(-9, 9, 120)])
    #测试集结果
    y_predict = network.feedforward(x_test)

    #图示对比训练集和测试集数据
    plt.plot(x,y,'r',x_test.T,y_predict.T,'*')
    plt.show()