如何实现基于商圈和地标的位置搜索
简介
标题中包含了两个关键词,商圈和地标,先来解释一下商圈和地标这两个名词。商圈是一个地理范围,但并不是官方的划分,而是民间大致的划分,它通常提供了民众消费、娱乐的功能,产生了一个相对集中的活动区域,比如王府井、五棵松。地标是地图上的一个点,它通常在某个范围有一定知名度,大家都知道它,它可以是一个大厦、景点、酒店、饭店,比如人民大会堂、北京工人体育场、大裤衩大楼等等。那实现这两个的搜索有什么好处呢?比如我打算去王府井溜达,提前订好吃饭的地方,就可以搜王府井附近有什么饭店,再比如我晚上去工人体育场看演唱会,提前订好住的地方,就可以搜索工人体育场附近有什么酒店。极大丰富了应用中的搜索场景。
商圈如何划定
地标不存在划定的问题,商圈的划定方式大体可以分为三类,多边形、矩形、圆形。
多边形
根据实际的商圈范围,划定边界,形成一个不规则形状。它的边界是由多个坐标点连线组成。
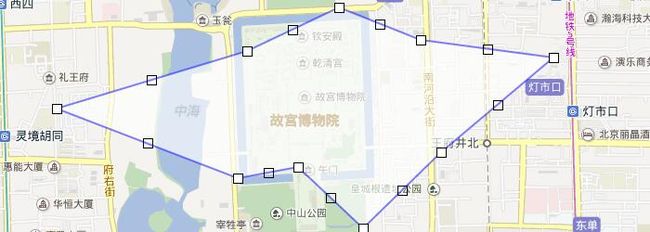
http://developer.baidu.com/map/jsdemo.htm#c2_9
存储时,需要将每个顶点坐标存下来。这样划分商圈会非常精确,就像官方的地理区域划分一样。但当判断一个坐标是否在这个商圈内的算法会比较复杂,可以先设定商圈内一个点X,然后将测定点P和X之间连线PX,如果PX跟商圈边界的交点是偶数个(0,2,4,…),则测定点P在商圈内;如果交点是奇数个(1,3,5,…),则测定点P在商圈外,可以参考java.awt.Polygon.contains的实现。
矩形
使用矩形来划定商圈,但矩形存在一个问题,就是不精确,容易划大或者划小,可以通过多个矩形来解决,精确度次于多边形。
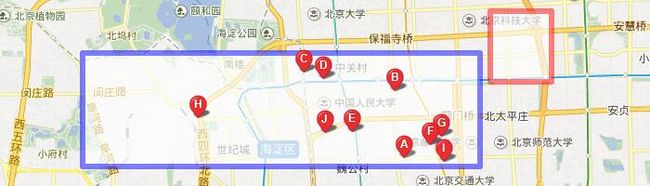
http://developer.baidu.com/map/jsdemo.htm#i1_2
存储时,需要将每个矩形的对角坐标存下来(对角坐标就能确定一个矩形)。判断一个坐标是否在这个商圈内时,直接判断测定点经纬度是否在矩形经纬度的范围内,多个矩形要判断多次。
圆形
使用圆形来划定商圈,圆形比较符合我们对商圈的理解,圈不就是圆嘛。圆形的问题和解决方式同矩形,精确度次于矩形。
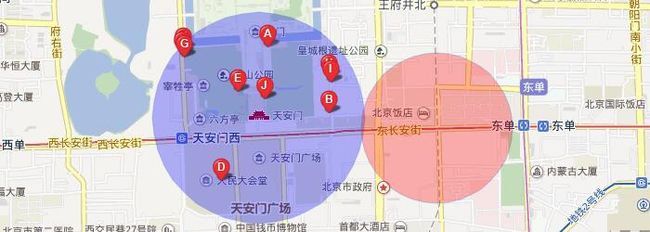
http://developer.baidu.com/map/jsdemo.htm#i3_2
存储时,需要将每个圆的圆心坐标和半径存下来。判断一个坐标是否在这个商圈内时,直接算测定点和圆心的距离,如果距离大于半径,则测定点在商圈外;否则在商圈内,多个圆要判断多次。
商圈搜索POI
接下来看一下如何根据商圈搜索POI,不同的划定方式实现是不一样的。
多边形
由于多边形的计算比较复杂,无法实时搜索。只能是将商圈和POI的关系提前建立好。
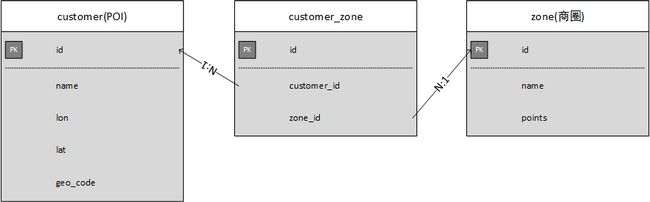
当新建或更新一个POI时,都需要判定它归属于哪个商圈,判定算法上面提到了,同样,当新建或更新一个商圈时,都需要计算哪些POI能归属到该商圈内,这时怎么计算呢?最笨的办法是遍历一次POI表,依次判断,但计算成本太高了,这里可以优化下,先取到商圈顶点坐标中最大经度、最小经度、最大纬度、最小纬度,这样就拿到了一个经纬度范围(商圈范围∈经纬度范围),然后再用经纬度范围到POI表中查找候选集,最后遍历这个候选集判断。
矩形&圆形
表结构同上,矩形和圆形都可以实时搜索,所以不需要POI和商圈的映射表。可以参照“如何实现按距离排序、范围查找”这篇文章,实现方式基本一致,这里不再赘述。
地标搜索POI
地标本身也是POI,它有一个坐标,这个问题就变成了“给定一个坐标,如何搜索附近POI”,也参照“如何实现按距离排序、范围查找”这篇文章。
总结
本文列举了三种方式去实现商圈搜索,现在从三个角度对比来看:
| # | 精确度 | 复杂度 | 灵活度 |
|---|---|---|---|
| 多边形 | 高 | 高 | 低 |
| 矩形 | 中 | 低 | 高 |
| 圆形 | 低 | 低 | 高 |
解释一下,精确度:很好理解,就是划定商圈的准确性,无疑多边形是最精准的;复杂度:实现的复杂性,包括前后端的整体实现;灵活度:其实是复杂度的一个延伸属性,复杂的实现肯定会丧失灵活度,比如多边形商圈更新会连带着POI也更新。通常情况下,我们O2O应用中对精确度都没有太高的要求,用户感知不到就好了,所以我建议采用矩形和圆形划定商圈,这样你会额外发现一个好处,所有基于位置去搜索POI的功能(离我最近、按商圈搜、按地标搜),底层的搜索实现都是同一个。如果对精确度有很高要求,只能选择多边形。
引用
http://stackoverflow.com/questions/8721406/how-to-determine-if-a-point-is-inside-a-2d-convex-polygon
http://developer.baidu.com/map/jsdemo.htm
本文来自:高爽|Coder,原文地址:http://blog.csdn.net/ghsau/article/details/51925755,转载请注明。