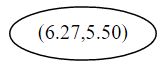【机器学习笔记】——k近邻（k-nearest neighbor，k-NN）

目 录

1 k-NN

  k近邻法（k-nearest neighbor，k-NN）是一种基本分类与回归算法。是一种消极学习法（直到给出新的数据才开始进行学习，否则仅存储训练集数据。而积极学习法是根据训练集数据提前训练好模型，当新的数据输入时通过模型进行预测）。

1.1 基本思路

  k-NN的想法非常简单，就是根据最近的k个样本来判断新的样本的分类或值，当模型是分类时用投票原则，当模型是回归时取平均数。显然有三个影响模型效果的三个因素：怎么衡量距离、怎么确定k值、怎么进行决策（如何投票）。此外因为算法是基于距离进行的，因此为了避免某些维度的尺度较大对结果产生额外的影响，需要对数据进行标准化处理

1.1.1 距离度量

  $L_p$距离（又称Minkowski距离）是一组距离。设特征空间 $\mathcal{X}$ 是 $n$ 维向量空间 ${\mathbf{R}}^n$ ， $x_i,x_j\in \mathcal{X}$ ， $x_i=(x_i^{(1)},x_i^{(2)},\cdots ,x_i^{(n)})$ ， $x_j=(x_j^{(1)},x_j^{(2)},\cdots ,x_j^{(n)})$ ， $x_i,x_j$ 的 $L_p$ 距离定义为

$$L_p(x_i,x_j)={\left(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^p\right)}^{\frac{1}{p}},p\ge 1$$

特别地，当 $p=2$ 时，称为欧氏距离，这也是我们比较常用的距离（当特征维度增加时，欧氏距离的结果会变差）：

$$L_2(x_i,x_j)={\left(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^2\right)}^{\frac{1}{2}}$$

当 $p=1$ 时，称为曼哈顿距离：

$$L_1(x_i,x_j)=\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}|$$

当 $p=\infty$ 时，称为切比雪夫距离：

$$L_{\infty }(x_i,x_j)=\underset{p\to \infty }{\lim }{\left(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^p\right)}^{\frac{1}{p}}=\underset{l}{\max }|x_i^{(l)}-x_j^{(l)}|$$

1.1.2 k值的选择

  当 $k$ 比较小时，学习的训练误差比较小，只有与输入实例较近的训练样本才会起作用，但是测试误差会比较大，模型的鲁棒性较差。一旦邻近的实例点恰巧是噪声，那么预测就会出错。也即是说模型会比较复杂，容易发生过拟合。特别地当 $k=1$ 时，k-NN又称最近邻算法。相反当 $k$ 比较大时，较远的样本点会起到作用，增加预测错误的概率，模型虽然简单但是容易欠拟合。特别地当 $k=N$ 时，无论输入什么实例，结果都是训练集数据中比例最大的类，是没有意义的。

  实际应用中通常采取交叉验证法来选取最优的 $k$ 值。

1.1.3 决策

  对于不含权重的数据，分类决策往往是多数表决。

1.2 基于kd树的k-NN算法

  k-NN算法的核心就是找到最近的k个实例点，前面的方法是线性扫描，显然效率是比较差的。而kd树（k-dimensional tree，注意k是特征维度，而不是k-NN中的k，kd树是一种数据结构，用来存储k维空间中的实例点以便对其进行快速检索）方法就可以节省很多时间。

1.2.1 构造kd树

  下面直接给出算法和一个例子便于理解如何构造kd树。

  输入：k维空间数据集$T=x_1,x_2,\cdots ,x_N$，其中$x_i=(x_i^{(1)},x_i^{(2)},\cdots ,x_i^{(k)}),i=1,2,\cdots ,N$

  输出：kd树

  (1) 选择一个坐标轴 $x^{(r)}$ （初始坐标轴一般是 $x^{(1)}$ ，或者选取数据方差最大的轴），然后找到该轴下数据的中位数据（如果数据个数为偶数，选择中位数据左边或右边的数据都可以）作为切分点（初始切分点即为根结点），并记录当前切分轴为通过切分点并与坐标轴 $x^{(r)}$ 垂直的超平面。由根节点生成深度为1的左、右子结点：左子结点对应坐标 $x^{(r)}$ 小于切分点的子区域，右子结点对应于坐标 $x^{(r)}$ 大于切分点的子区域。将落在切分超平面上的实例点保存在根结点。

  (2) 重复：选择坐标轴 $x^{(r)}$ （$r\leftarrow r\mathrm{m}\mathrm{o}\mathrm{d}k+1$）。同样方式寻找切分点。

  (3) 直到两个子区域没有实例存在时停止

  注意结点应该是一块超矩形区域，而不是数据点，结点中可能包含不止一个数据点。例如根结点是最初的整个矩形而不是第一个切分点。

  实例  给定一个二维空间的数据集：

$$T=(-4.60,-10.55{)}^T,(-4.96,12.61{)}^T,(1.75,12.26{)}^T,(15.31,-13.16{)}^T,(7.83,15.70{)}^T,(14.63,-0.35{)}^T,(-6.88,-5.40{)}^T,(-2.96,-0.50{)}^T,(7.75,-22.68{)}^T,(10.80,-5.03{)}^T,(1.24,-2.86{)}^T,(17.05,-12.79{)}^T,(6.27,5.50{)}^T$$

构造一个kd树

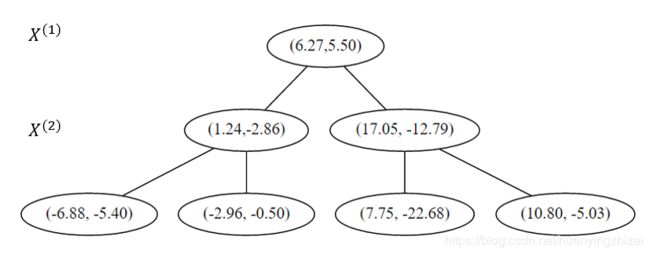
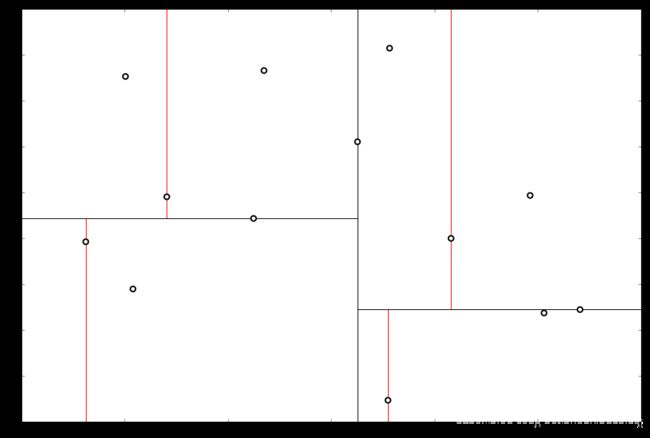
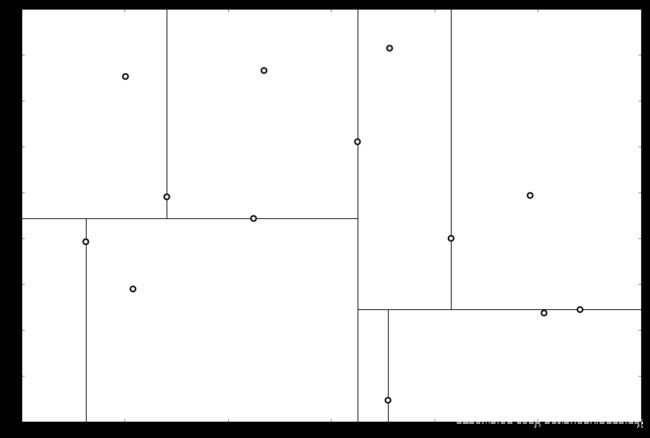
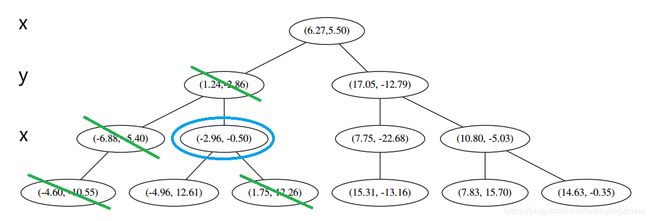
  解 选择初始坐标轴为 $x^{(1)}$ 轴（$r=1$），选择该轴下的中位数据 $(6.27,5.50{)}^T$作为根结点，并且按照该点的 $x^{(1)}$ 坐标将空间进行切分，所有 $x^{(1)}$ 坐标小于 6.27 的数据用于构建左枝，$x^{(1)}$ 坐标大于 6.27 的点用于构建右枝。

  在下一步中 $r=r\mathrm{m}\mathrm{o}\mathrm{d}2+1=2$ 对应 $x^{(2)}$ 轴，左右两边再按照 $x^{(2)}$ 轴的排序进行切分，中位点记载于左右枝的节点。得到下面的树，左边的 $x^{(1)}$ 是指这该层的节点都是沿 $x^{(1)}$ 轴进行分割的。

  下一步中 $r=r\mathrm{m}\mathrm{o}\mathrm{d}2+1=1$，对应 $x^{(1)}$ 轴，所以下面再按照 $x^{(1)}$ 坐标进行排序和切分，有

  最后每一部分都只剩一个点，将他们记在最底部的节点中。因为不再有未被记录的点，所以不再进行切分。

  就此完成了 kd 树的构造。

1.2.2 搜索kd树（基于kd树的k-NN算法）

  简单来说搜索最近邻就是要找到包含目标数据的叶结点（矩形区域）；然后从该结点出发，依次退回到父结点；不断查找与目标点最邻近的结点，当确定不可能存在更近的结点时终止。

1.2.2.1 基于kd树的最近邻算法

  基于kd树的最近邻算法（k = 1）如下：

  输入：已构造的kd树；目标点 $x$

  输出：$x$ 的最近邻

  (1) 在kd树中找到包含目标点 $x$ 的叶结点：从根结点出发，递归地向下访问kd树。若目标点 $x$ 当前维的坐标小于切分点的坐标，则移动到左子结点，否则移动到右子结点。直到子结点为叶结点为止。

  (2) 以此叶结点为“当前最近点”

  (3) 递归地向上回推，更新“当前最近点”

  (a) 如果该结点保存的实例点比“当前最近点”距离目标点更近，则以该实例点为“当前最近点”

  (b) “当前最近点”一定存在于该结点一个子结点对应的区域。检查该子结点的兄弟结点对应的区域是否有更近的点。具体地，检查兄弟结点对应的区域是否以目标点为球心、以目标点与“当前最近点”间的距离为半径的超球体相交。如果相交，可能在兄弟结点对应的区域内存在距目标点更近的点，移动到兄弟结点。接着递归地进行最近邻搜索；如果不相交，向上回退。

  (4) 当回退到根结点时，搜索结束。最后的“当前最近点”即为x的最近邻点。

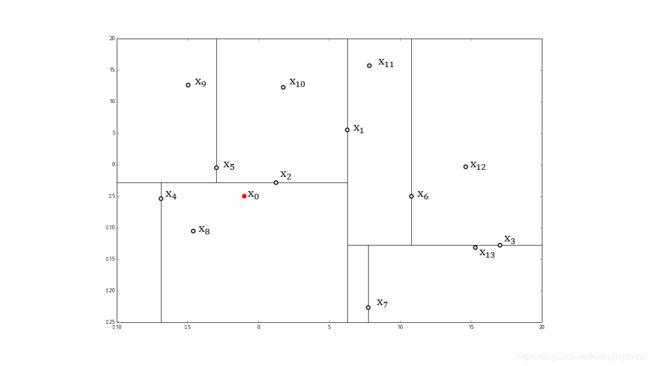
  实例  基于前面的实例找到目标点 $x_0=(-1,5)$ 的最近邻

  解 先为各数据点标号便于说明

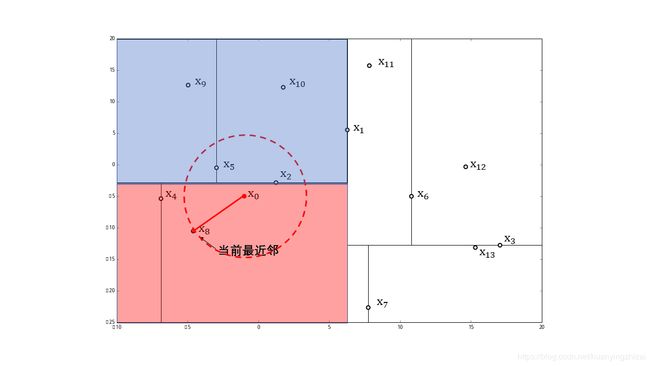
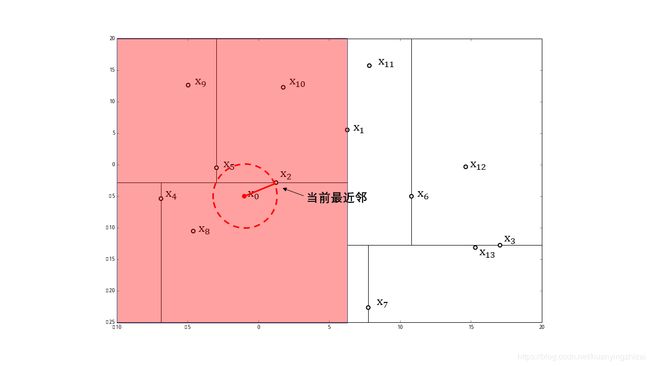
  在kd树中找到包含点 $x_0$ 的叶节点 $x_8$ （图中红色区域），以点 $x_8$ 作为近似最近邻。那么真实最近邻一定在以点 $x_0$ 为中心通过 $x_8$ 的圆的内部

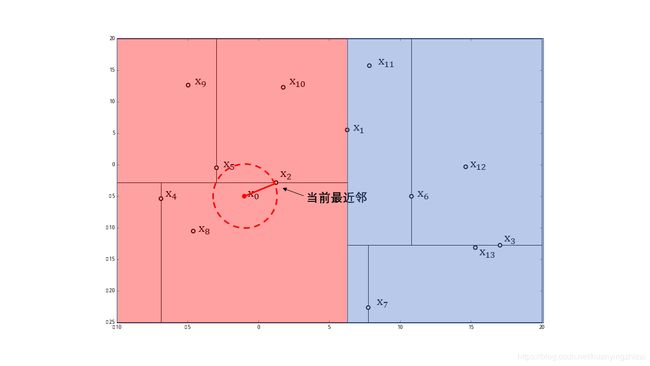
  然后返回点 $x_0$ 的父结点 $x_4$ ，在结点 $x_4$ 的另一子结点区域（图中蓝色区域）内搜索最近邻。该区域与圆不相交，不可能有最近邻点。

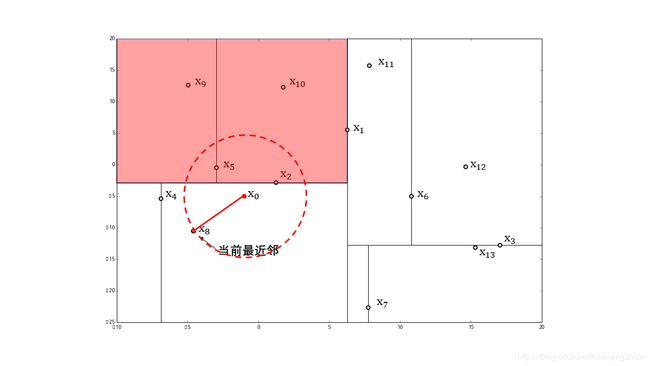
  继续返回上一级父结点 $x_2$ ，实例点 $x_2$不在圆中。在结点 $x_2$ 的另一子结点 $x_5$ 的区域内搜索最近邻

  结点 $x_5$ 的区域与圆相交，移动到该结点

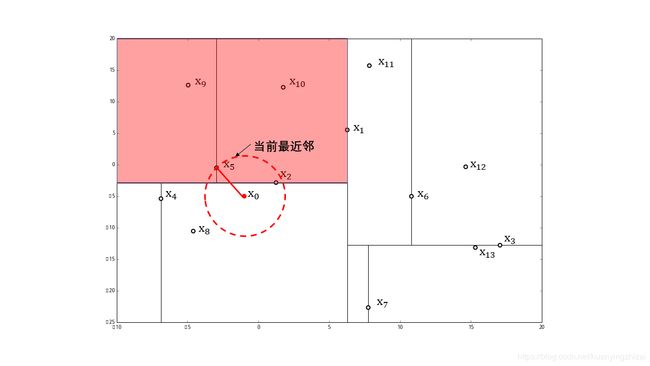
  该区域在圆内的实例点有 $x_5$，比点 $x_8$ 更近，成为新的近似最近邻

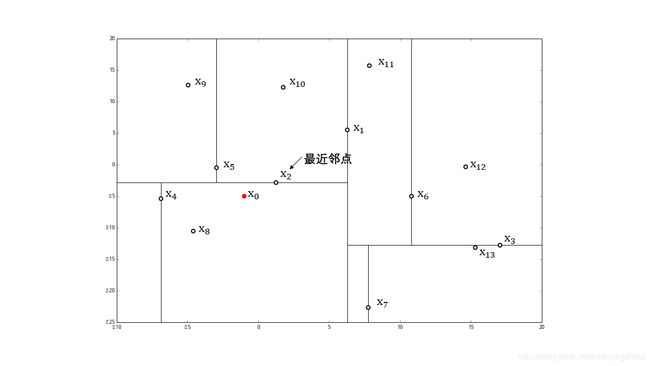
  移动到父结点 $x_2$ ，实例点 $x_2$ 在圆中，且比点 $x_5$ 更近，成为新的近似最近邻

  然后返回点 $x_2$ 的父结点 $x_1$，在结点 $x_1$ 的另一子结点区域（图中蓝色区域）内搜索最近邻。该区域与圆不相交，不可能有最近邻点。最后确定点 $x_2$ 是目标点 $x_0$ 的最近邻

1.2.2.2 基于kd树的k-NN算法

  基于kd树的k近邻算法可以看作是基于kd树的最近邻算法的推广，只不过需要事先建立一个用于存放 k 近邻的列表 L，然后把 L 中距离目标点最远点点看作是最近邻进行更新。具体算法如下：

  (一) 根据目标点的坐标值和每个结点的切分向下搜索。

  (二) 当达到一个底部结点时，将其标记为访问过。如果 L 里不足 k 个点，则将当前结点的特征坐标加入 L ；如果 L 不为空并且当前结点 的特征与目标点的距离小于 L 里最长的距离，则用当前特征替换掉 L 中离目标点最远的点。

  (三) 如果当前节点不是整棵树最顶端节点，执行 (a)；反之，输出 LLL，算法完成。

  (a) 向上爬一个结点。如果当前（向上爬之后的）结点未曾被访问过，将其标记为被访问过，然后执行 ① 和 ②；如果当前节点被访问过，再次执行 (a)。

   ① 如果此时 L 里不足 k 个点，则将结点特征加入 L；如果 L 中已满 k 个点，且当前结点与目标点的距离小于 L 里最长的距离，则用结点特征替换掉 LLL 中离最远的点。

   ② 计算目标点和当前结点切分线的距离。如果该距离大于等于 L 中距离目标点最远的距离并且 L 中已有 k 个点，则在切分线另一边不会有更近的点，执行(三)；如果该距离小于 L 中最远的距离或者 L 中不足 k 个点，则切分线另一边可能有更近的点，因此在当前节点的另一个枝从 (一) 开始执行。

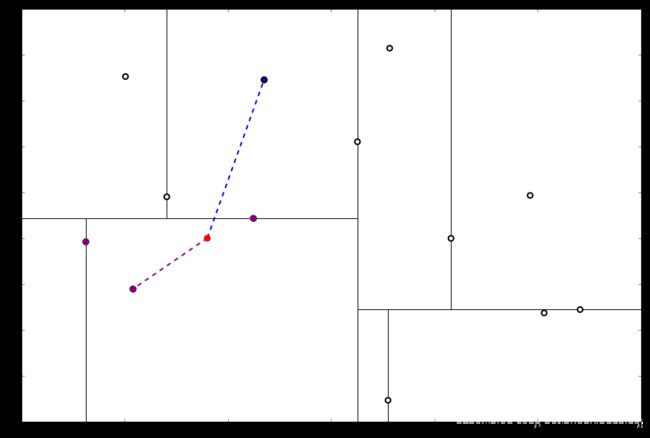
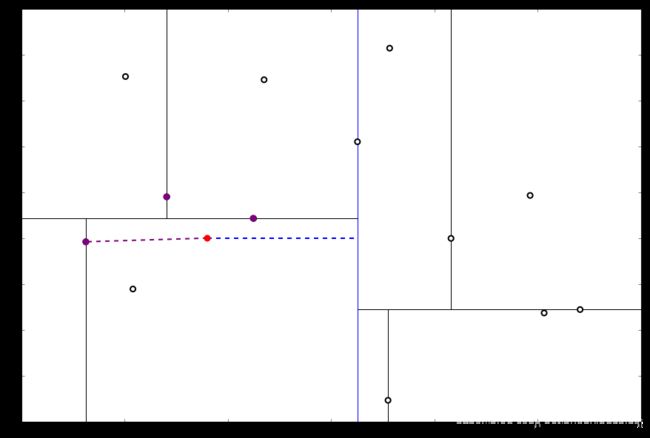
  实例  基于前面的实例，我们寻找目标点 $x_0$ 的 3 个近邻

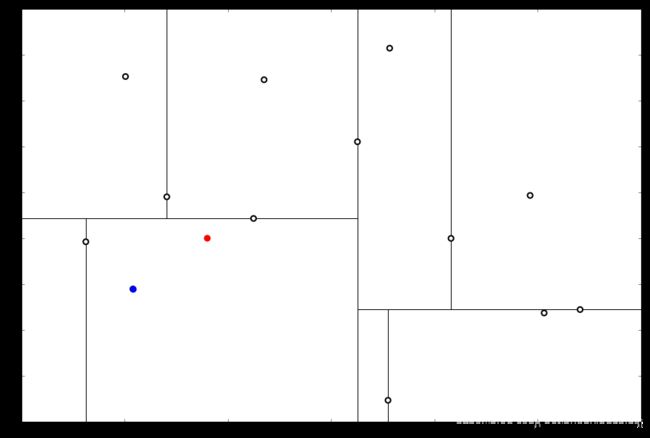
  解 首先执行(一)，我们按照切分找到最底部节点。首先，我们在顶部开始

  和这个节点的 x 轴比较一下

  $x_0$ 的 x 值更小。因此我们向左枝进行搜索

  这次对比 y 轴

  $x_0$ 的 y 值更小，因此向左枝进行搜索

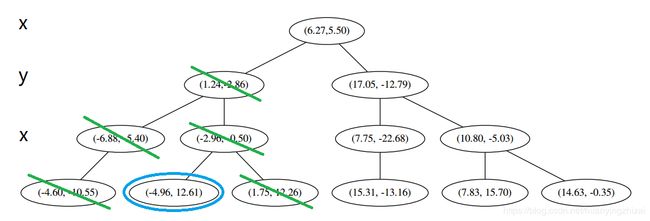
  这个结点只有一个子枝，就不需要对比了。由此找到了最底部的结点 $x_8=(-4.6,-10.55)$

  在二维图上是

  此时我们执行 (二)。将当前结点标记为访问过，并记录下 $L=[(-4.6,-10.55)]$。访问过的结点就在二叉树上显示为被划掉好了。

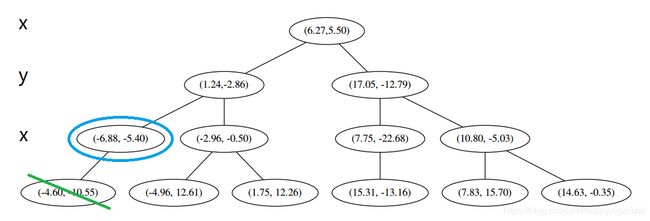
  然后执行 (三)。不是最顶端结点。好，执行 (a)，我爬。上面的是 $x_4=(-6.88,-5.4)$。

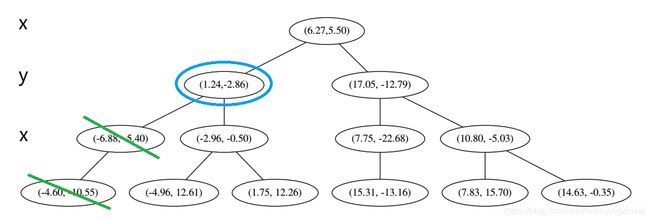
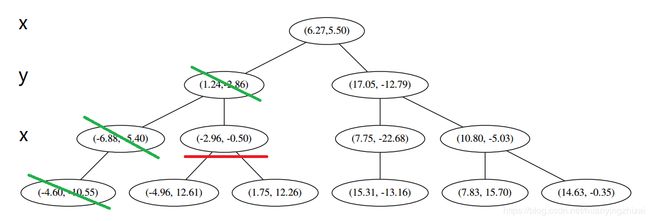
  执行 ①，因为我们记录下的点只有一个，小于 $k=3$，所以也将当前节结记录下，有 $L=[(-4.6,-10.55),(-6.88,-5.4)]$。再执行 ②，因为当前结点的左枝是空的，所以直接跳过，回到步骤 (三)。好，不是顶部，执行(a)。

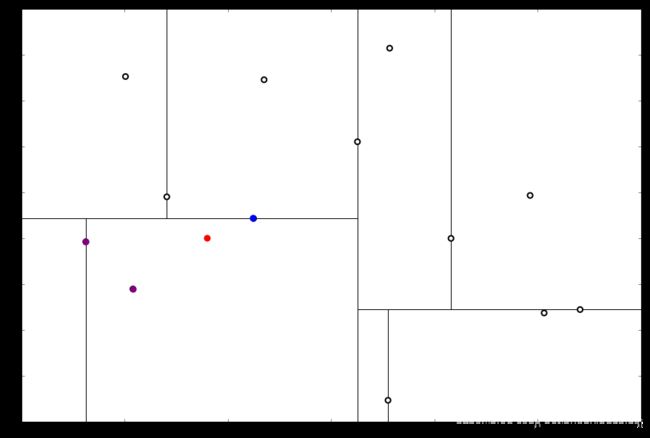
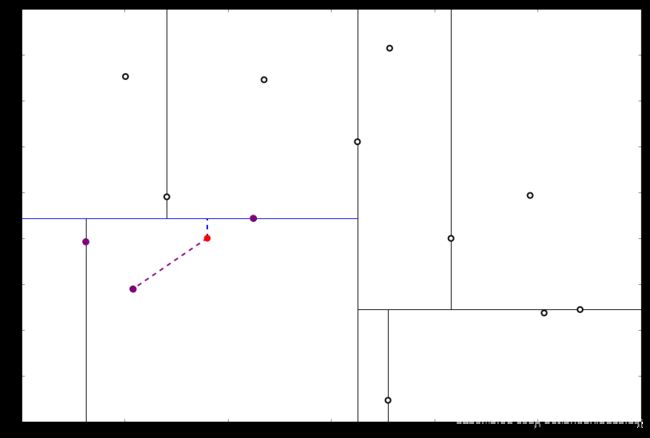
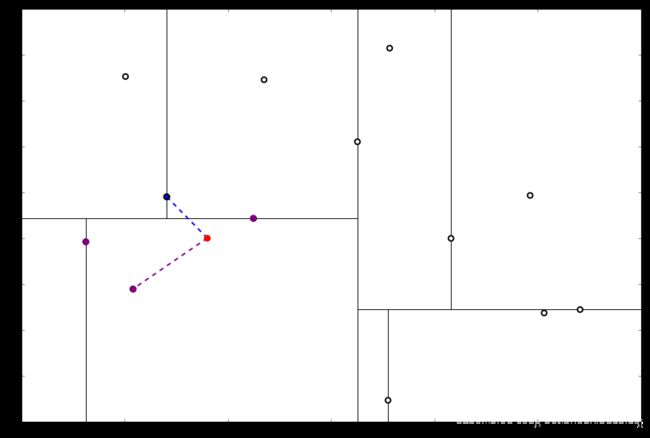
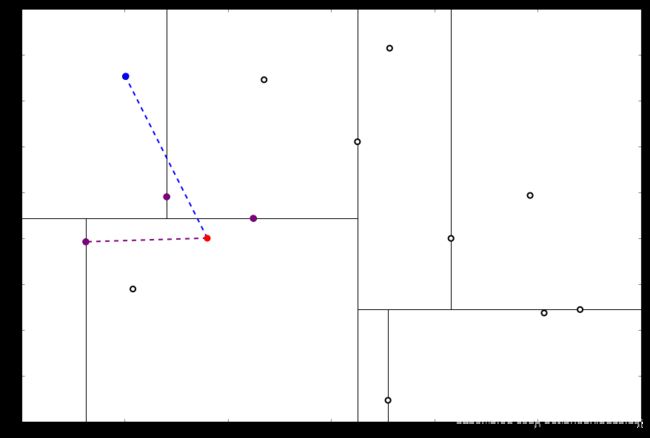
  执行①，由于还是不够三个点，于是将当前点也记录下，有 $L=[(-4.6,-10.55),(-6.88,-5.4),(1.24,-2.86)]$。当然，当前结点变为被访问过的。再执行②，发现当前结点有其他的分枝，并且经计算得出目标点 $x_0$ 和 L 中的三个点的距离分别是 $6.62,5.89,3.10$，但是目标点和当前结点的分割线的距离只有 $2.14$，小于与 L 的最大距离：

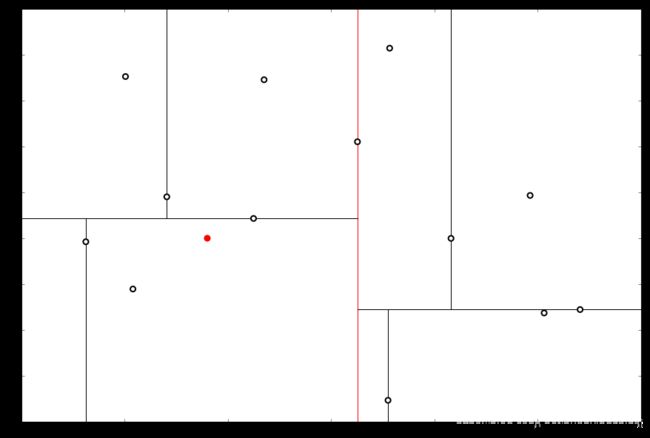
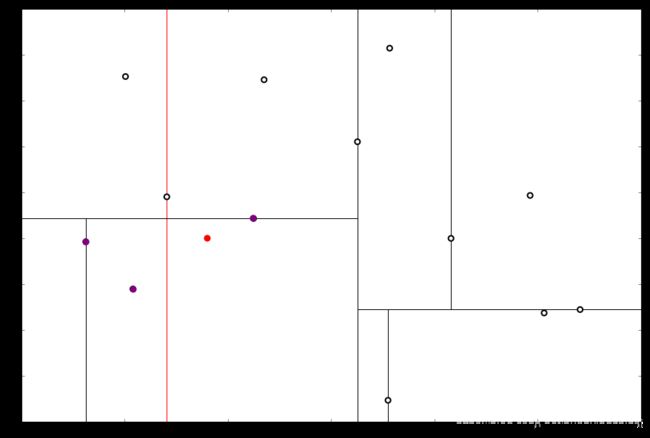
  因此，在分割线的另一端可能有更近的点。于是我们在当前结点的另一个分枝从头执行 (一)。好，我们在红线这里：

  要用目标点和这个结点比较 x 坐标:

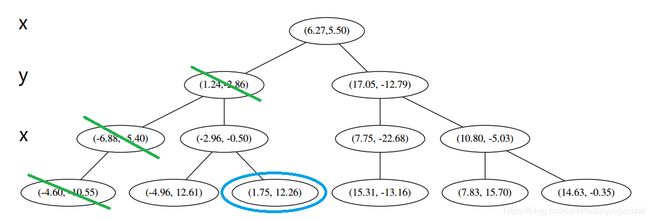
  $x_0$ 的 x 值更大，因此探索右枝，并且发现右枝已经是最底部结点，因此启动 (二)。

  经计算，$x_{1}0=(1.75,12.26)$ 与 $x_0$ 的距离是 17.48，要大于 $x_0$ 与 L 的最大距离，因此我们不将其放入记录中

  执行 (三) 判断出不是顶端结点，执行(a)。

  执行①，该结点与 $x_0$ 的距离是 4.91，要小于 $x_0$ 与 L 的最大距离 6.62。

  因此，我们用这个新的结点 $x_5$ 替代 L 中离 $x_0$ 最远的 $x_8=(-4.6,-10.55)$。

  然后继续执行②，我们比对 $x_0$ 和当前结点的分割线的距离

  这个距离小于 L 与 $x_0$ 的最小距离，因此我们要到当前节点的另一个枝执行 (一)。当然，那个枝只有一个点，直接到 (二)。

  计算距离发现这个点离 $x_0$ 比 L 更远，因此不进行替代。

  执行(三) 发现不是顶点，所以呼出 (a)。我们向上爬

  这个是已经访问过的了，所以再来（a）

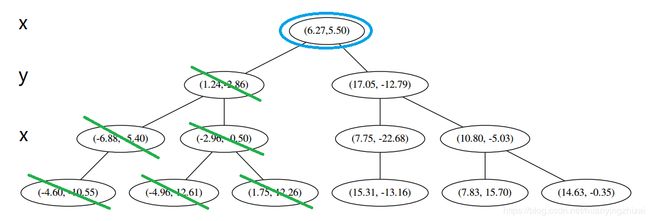
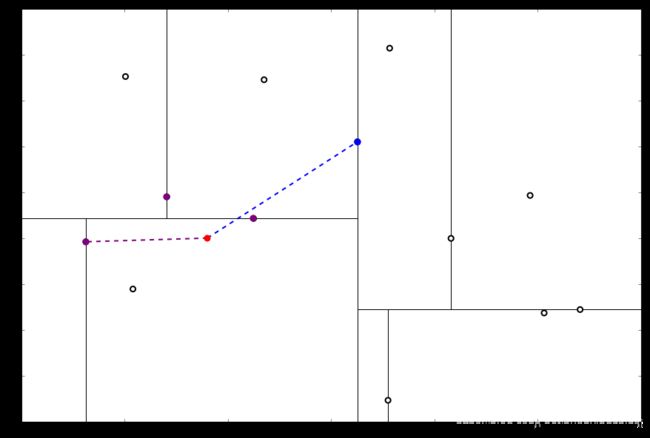
  好，再爬

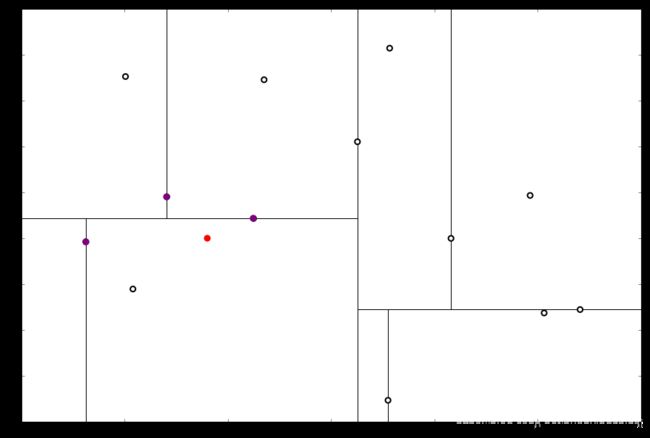
  啊！到顶点了。所以完了吗？当然不，还没轮到 (三) 呢。现在是 ① 的回合。我们进行计算比对发现顶端结点与 $x_0$ 的距离比 L 还要更远，因此不进行更新。

  然后是 ②，计算 $x_0$ 和分割线的距离发现也是更远。

  因此也不需要检查另一个分枝。然后执行 (三)，判断当前结点是顶点，因此计算完成！输出距离 $x_0$ 最近的三个样本是 $L=[(-6.88,-5.4),(1.24,-2.86),(-2.96,-2.5)]$。

1.3 k-NN的优缺点

1.3.1 优点

1.3.2 缺点

1. 必须保存全部数据（空间复杂度$O(n)$）

2. 计算耗时长（原始形式的时间复杂度$O(n)$，基于kd树的时间复杂度$O(\log n)$）

3. 无法给出任何数据结构信息（无法知道普通实例和典型实例具有怎样的特征）

2 算法实现

2.1 原始形式1——自定义二维特征分类数据

import numpy as np

class myknn:
    def __init__(self, data, label, x, k = 3, d = 'l2'):
        self.data, rangedata, mindata = self.ori2norm(data)
        self.label = label
        #self.x = self.ori2norm(x)    # 这里应该用训练数据的最大最小值对测试数据进行归一化，不能直接对单个数据进行归一化
        self.x = (x - mindata)/rangedata
        self.k = k
        self.d = d
        
    @staticmethod
    def ori2norm(mat):
        '''
        训练集归一化函数
        '''
        minv = mat.min(axis = 0)
        maxv = mat.max(axis = 0)
        rangev = maxv - minv

        normmat = (mat - np.tile(minv, (mat.shape[0], 1)))/(maxv - minv)
        return normmat, rangev, minv

    def caldistance(self):
        '''
        计算距离
        返回以[距离，序号]为元素的列表
        '''
        if self.d == 'l2':
            N = self.data.shape[0]
            l = self.data.shape[1]
            dis = np.zeros(shape = (N, l))
            for i in range(N):
                idis = 0
                for j in range(l):
                    idis += (self.data[i][j] - self.x[j])**2
                idis = idis**0.5
                dis[i] = [idis, i]
            return dis
        
    def predict(self, printneighbor = False):
        '''
        预测函数
        '''
        sortdis = self.caldistance()
        sortdis = sortdis[sortdis[:, 0].argsort()]
        labeldict = {}
        for index in range(self.k):
            label = self.label[int(sortdis[index][1])]
            labeldict[label]  = labeldict.get(label, 0) + 1
            if printneighbor == True:
                print('第%i个近邻为%s'%(index+1, label))
        pre = max(labeldict,key = labeldict.get)    # 若票数相同，只能返回第一个最多票数的标签
        print('\n分类结果为：%s'%pre)
        return pre
            
if __name__ == '__main__':
    data = np.array([[1, 101], [5, 89], [108, 5], [115, 8], [30, 62], [40, 57]])
    labels = ['oarnge', 'orange', 'apple', 'apple', 'banana', 'banana']
    x = np.array([101, 20])
    clf = myknn(data = data, label = labels, x = x, k = 3)
    clf.predict(printneighbor = True)

第1个近邻为apple
第2个近邻为apple
第3个近邻为banana

分类结果为：apple

2.2 原始形式2——自定义二维特征分类数据

参考：Eric量化交易的知乎，源代码未对数据进行归一化处理

import numpy as np
import operator

def createDataSet():
    '''
    函数说明: 创建数据集
    Returns:
    group - 数据集
    labels - 分类标签
    '''
    group=np.array([[1,101],[5,89],[108,5],[115,8],[30,62],[40,57]]) #数据集，四组二维特征
    labels=['oarnge','orange','apple','apple','banana','banana'] #分类标签，四组特征的标签
    return group,labels

def classify0(inX, dataSet, labels, k):
    """
    函数说明:kNN算法,分类器
    Parameters:
    inX - 待预测数据
    dataSet - 用于训练的数据(训练集)
    labes - 分类标签
    k - kNN算法参数,选择距离最小的k个点
    Returns:
    sortedClassCount[0][0] - 分类结果
    """
    N = dataSet.shape[0]
    diffMat = np.tile(inX, (N, 1)) - dataSet    # 待测数据与训练集的差
    sqDiffMat = diffMat ** 2
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances ** 0.5    # 欧氏距离
    sortedDistIndices = distances.argsort()   # 距离从小到大排序后的在原序列中的索引值
    
    classCount = {}
    for i in range(k):
        voteIlabel = labels[sortedDistIndices[i]]
        print('第', i+1, '个近邻是', voteIlabel)
        classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
    
    # key=operator.itemgetter(1)根据字典的值进行排序
    # key=operator.itemgetter(0)根据字典的键进行排序
    # reverse降序排序字典
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    
    return sortedClassCount[0][0]
 
 
if __name__ == '__main__':
    group, labels = createDataSet()
    test = [101, 20]
    test_class = classify0(test, group, labels, 3)
    print('k-NN分类结果为', test_class)

第 1 个近邻是 apple
第 2 个近邻是 apple
第 3 个近邻是 banana
k-NN分类结果为 apple

2.3原始形式3——改进约会网站的配对效果（三维特征）

参考：qwertWZ的博客

import pandas as pd
import numpy as np
import operator
import matplotlib.pyplot as plt

2.3.1 导入数据

  我的朋友海伦一直使用在线约会网站寻找适合自己的约会对象。尽管约会网站会推荐不同的人选，但她并不是喜欢每一个人。经过一番总结，她发现曾交往过三种类型的人：

• 不喜欢的人
• 魅力一般的人
• 极具魅力的人

  海伦希望我们的分类软件可以更好地帮助她将匹配对象划分到确切的分类中。此外海伦还收集了一些约会网站未曾记录的数据信息，她认为这些数据更有助于匹配对象的归类。

  数据存放在文本文件datingTestSet.txt中，每个样本数据占据一行，总共有1000行。

  海伦的样本主要包含以下3种特征：

• 每年获得的飞行常客里程数
• 玩视频游戏所耗时间百分比
• 每周消费的冰淇淋公升数

  在将上述特征数据输入到分类器之前，必须将待处理数据的格式改变为分类器可以接受的格式。

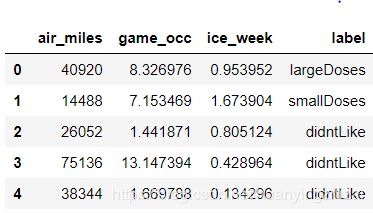
df = pd.read_table('file/datingTestSet.txt', header = None, names = ['air_miles', 'game_occ', 'ice_week', 'label'], sep = '\t')
df.head()

# 提取特征和标签
featuremat = df.iloc[:, :-1]
labellist = df.iloc[:, -1]

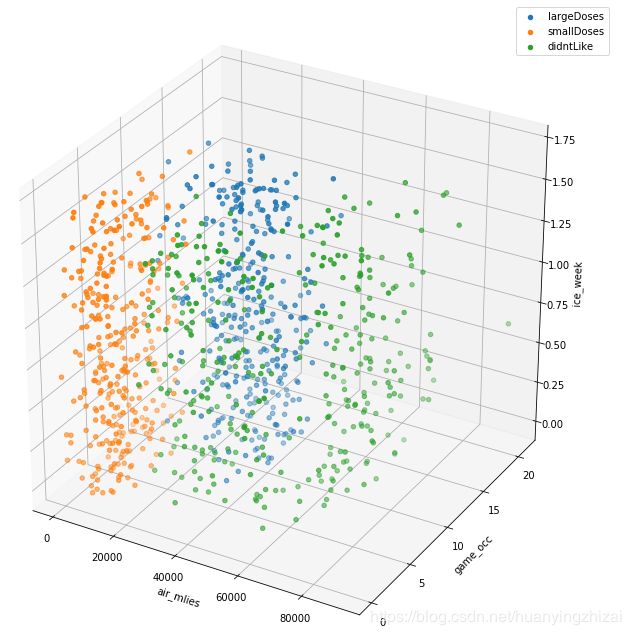
# 查看三维散点图
from mpl_toolkits.mplot3d import Axes3D

# 定义三维坐标轴
fig = plt.figure(figsize = (12,12))
ax = plt.axes(projection = '3d')
ax.set_xlabel('air_mlies')
ax.set_ylabel('game_occ')
ax.set_zlabel('ice_week')

xl = df['air_miles'][df.label=='largeDoses']    # 极具魅力的人实例
yl = df['game_occ'][df.label=='largeDoses']
zl = df['ice_week'][df.label=='largeDoses']
xs = df['air_miles'][df.label=='smallDoses']    # 一般魅力的人实例
ys = df['game_occ'][df.label=='smallDoses']
zs = df['ice_week'][df.label=='smallDoses']
xd = df['air_miles'][df.label=='didntLike']    # 不喜欢的人实例
yd = df['game_occ'][df.label=='didntLike']
zd = df['ice_week'][df.label=='didntLike']

ax.scatter(xl, yl, zl, label = 'largeDoses')
ax.scatter(xs, ys, zs, label = 'smallDoses')
ax.scatter(xd, yd, zd, label = 'didntLike')

plt.legend()

plt.show()

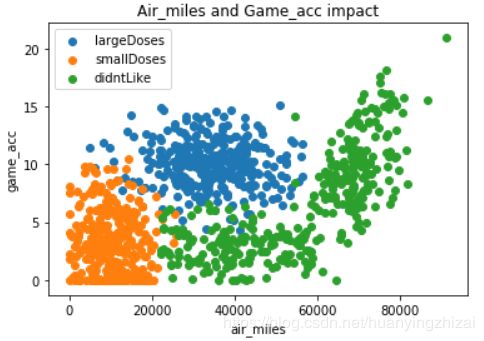
# 查看不同特征组合下的散点图
plt.figure(2)
plt.title('Air_miles and Game_acc impact')
plt.xlabel('air_miles')
plt.ylabel('game_acc')

plt.scatter(xl, yl, label = 'largeDoses')
plt.scatter(xs, ys, label = 'smallDoses')
plt.scatter(xd, yd, label = 'didntLike')

plt.legend()
plt.show()

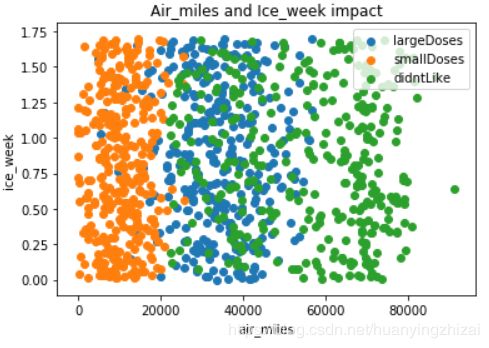
plt.figure(3)
plt.title('Air_miles and Ice_week impact')
plt.xlabel('air_miles')
plt.ylabel('ice_week')

plt.scatter(xl, zl, label = 'largeDoses')
plt.scatter(xs, zs, label = 'smallDoses')
plt.scatter(xd, zd, label = 'didntLike')

plt.legend()
plt.show()

plt.figure(4)
plt.title('Game_acc and Ice_week impact')
plt.xlabel('game_acc')
plt.ylabel('ice_week')

plt.scatter(yl, zl, label = 'largeDoses')
plt.scatter(ys, zs, label = 'smallDoses')
plt.scatter(yd, zd, label = 'didntLike')

plt.legend()
plt.show()

  可见飞行里程和游戏时间两个特征对数据的分类效果更好

2.3.2归一化处理

  不同特征值有不同的均值和取值范围，如果直接使用特征值计算距离，取值范围较大的特征将对距离计算的结果产生绝对得影响，而使较小的特征值几乎没有作用，近乎没有用到该属性。在处理这种不同取值范围的特征值时，我们通常采用的方法是将数值归一化，如将取值范围处理为0到1或者-1到1之间。下面的公式可以将任意取值范围的特征值转化为0到1区间内的值：

$$\text{newValue}=(\text{oldValue}–min)/(max–min)$$

  其中min和max分别是数据集中的最小特征值和最大特征值

def ori2norm(mat):
    minv = mat.min(axis = 0)
    maxv = mat.max(axis = 0)
    ranges = maxv - minv

    normmat = (mat - np.tile(minv, (mat.shape[0], 1)))/(maxv - minv)
    return normmat, minv, ranges

normfeature, minf, rangef = ori2norm(featuremat)
normfeature.head()

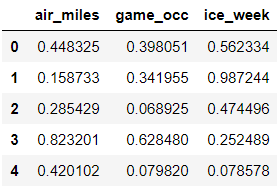
  要注意返回结果除了归一化好的数据，还包括用来归一化的范围值ranges和最小值minVals，这将用于对测试数据的归一化。

  注意，对测试数据集的归一化过程必须使用和训练数据集相同的参数（ranges和minVals），不能针对测试数据单独计算ranges和minVals，否则将造成同一组数据在训练数据集和测试数据集中的不一致。

2.3.3构建k-NN分类模型

def myknn(inpdata, traindata, labels, k):
    # 先对输入数据进行标准化
    norminpdata = (inpdata - minf)/rangef
    
    size = traindata.shape[0]
    minusmat = (np.tile(norminpdata, (size, 1)) - traindata)**2
    dismat = minusmat.sum(axis = 1)**0.5
    
    sortindex = dismat.argsort()
    neighbordict = {}
    for i in range(k):
        neighborlabel = labellist[sortindex[i]]
        neighbordict[neighborlabel] = neighbordict.get(neighborlabel, 0) + 1
        
    sortedClassCount = sorted(neighbordict.items(), key = operator.itemgetter(1), reverse = True)
        
    return sortedClassCount[0][0]

2.3.4预测

test = np.array([10000, 10, 0.1])
myknn(test, featuremat, labellist, 3)

‘smallDoses’

2.4 基于kd树的k-NN算法——自定义二维分类特征数据

参考：wenffe的博客

"""
构建kd树，提高KNN算法的效率（数据结构要自己做出来才有趣）
    1. 使用对象方法封装kd树
    2. 每一个结点也用对象表示，结点的相关信息保存在实例属性中
    3. 使用递归方式创建树结构以及实现树的其它逻辑结构
"""
 
import numpy as np
import time

class Node(object):
    '''
    结点对象
    '''
    def __init__(self, item=None, label=None, dim=None, parent=None, left_child=None, right_child=None):
        self.item = item   # 结点的值(样本信息)
        self.label = label  # 结点的标签
        self.dim = dim   # 结点的切分的维度(特征)
        self.parent = parent  # 父结点
        self.left_child = left_child  # 左子树
        self.right_child = right_child # 右子树


class KDTree(object):
    '''
    kd树
    '''
 
    def __init__(self, aList, labelList):
        self.__length = 0  # 不可修改
        self.__root = self.__create(aList,labelList)  # 根结点, 不可修改
 
    def __create(self, aList, labelList, parentNode=None):
        '''
        构造kd树
        Parameter：
            param aList: 需要传入一个类数组对象(行数表示样本数，列数表示特征数)
            labellist: 样本的标签
            parentNode: 父结点
        Return: 
            根结点
        '''
        dataArray = np.array(aList)
        m,n = dataArray.shape
        labelArray = np.array(labelList).reshape(m,1)
        
        
        if m == 0:  # 样本集为空
            return None
        
        # 确定初始切分超平面
        # 求所有特征的方差，选择最大的那个特征作为切分超平面
        var_list = [np.var(dataArray[:,col]) for col in range(n)]
        max_index = var_list.index(max(var_list))    # 获取最大方差特征的索引
        
        max_feat_ind_list = dataArray[:,max_index].argsort()    # 按照前面得到的维度对所有数据进行排列，返回索引
        mid_item_index = max_feat_ind_list[m // 2]    # 取出中位数据的索引
        
        
        if m == 1:  # 样本为1时，返回自身
            self.__length += 1
            return Node(dim = max_index,
                        label = labelArray[mid_item_index], 
                        item = dataArray[mid_item_index], 
                        parent = parentNode, 
                        left_child = None, 
                        right_child = None)
 
        # 生成结点
        node = Node(dim = max_index,
                    label = labelArray[mid_item_index], 
                    item = dataArray[mid_item_index], 
                    parent = parentNode, 
                    left_child = None, 
                    right_child = None)
        
        # 构建有序的子树
        left_tree = dataArray[max_feat_ind_list[:m // 2]] # 左子树
        left_label = labelArray[max_feat_ind_list[:m // 2]] # 左子树标签
        left_child = self.__create(left_tree, left_label, node)
        
        if m == 2:  # 只有左子树，无右子树
            right_child = None
            
        else:
            right_tree = dataArray[max_feat_ind_list[m // 2 + 1:]] # 右子树
            right_label = labelArray[max_feat_ind_list[m // 2 + 1:]] # 右子树标签
            right_child = self.__create(right_tree,right_label,node)
            # self.__length += 1
            
        # 左右子树递归调用自己，返回子树根结点
        node.left_child=left_child
        node.right_child=right_child
        self.__length += 1
        return node
 
    @property
    def length(self):
        return self.__length
 
    @property
    def root(self):
        return self.__root
 
    def transfer_dict(self,node):
        '''
        查看kd树结构
        Parameter：
            node:需要传入根结点对象
        Return: 字典嵌套格式的kd树,字典的key是self.item,其余项作为key的值，类似下面格式
            {(1,2,3):{
                    'label':1,
                    'dim':0,
                    'left_child':{(2,3,4):{
                                         'label':1,
                                         'dim':1,
                                         'left_child':None,
                                         'right_child':None
                                        },
                    'right_child':{(4,5,6):{
                                            'label':1,
                                            'dim':1,
                                            'left_child':None,
                                            'right_child':None
                                            }
                    }
        '''
        if node == None:
            return None
        kd_dict = {}
        kd_dict[tuple(node.item)] = {}  # 将自身值作为key
        kd_dict[tuple(node.item)]['label'] = node.label[0]
        kd_dict[tuple(node.item)]['dim'] = node.dim
        kd_dict[tuple(node.item)]['parent'] = tuple(node.parent.item) if node.parent else None
        kd_dict[tuple(node.item)]['left_child'] = self.transfer_dict(node.left_child)
        kd_dict[tuple(node.item)]['right_child'] = self.transfer_dict(node.right_child)
        return kd_dict
 
    def transfer_list(self,node, kdList=[]):
        '''
        将kd树转化为嵌套字典的列表输出
        Parameter：
            node: 需要传入根结点
        Return: 返回嵌套字典的列表，格式如下
            [{'item': (9, 3),
                 'label': 1,
                 'dim': 0,
                 'parent': None,
                 'left_child': (3, 4),
                 'right_child': (11, 11)
             },
             {'item': (3, 4),
                'label': 1,
                'dim': 1,
                'parent': (9, 3),
                'left_child': (7, 0),
                'right_child': (3, 15)
             }]
        '''
        if node == None:
            return None
        element_dict = {}
        element_dict['item'] = tuple(node.item)
        element_dict['label'] = node.label[0]
        element_dict['dim'] = node.dim
        element_dict['parent'] = tuple(node.parent.item) if node.parent else None
        element_dict['left_child'] = tuple(node.left_child.item) if node.left_child else None
        element_dict['right_child'] = tuple(node.right_child.item) if node.right_child else None
        kdList.append(element_dict)
        self.transfer_list(node.left_child, kdList)
        self.transfer_list(node.right_child, kdList)
        return kdList
 
    def _find_nearest_neighbour(self, item):
        '''
        找最近邻点
        Parameter：
            item:需要预测的新样本
        Return: 距离最近的样本点
        '''
        itemArray = np.array(item)
        if self.length == 0:  # 空kd树
            return None
        # 递归找离测试点最近的那个叶结点
        node = self.__root
        if self.length == 1: # 只有一个样本
            return node
        while True:
            cur_dim = node.dim
            if item[cur_dim] == node.item[cur_dim]:
                return node
            elif item[cur_dim] < node.item[cur_dim]:  # 进入左子树
                if node.left_child == None:  # 左子树为空，返回自身
                    return node
                node = node.left_child
            else:
                if node.right_child == None:  # 右子树为空，返回自身
                    return node
                node = node.right_child
 
    def knn_algo(self, item, k=1):
        '''
        找到距离测试样本最近的前k个样本
        Parameter：
            item: 测试样本
            k: knn算法参数，定义需要参考的最近点数量，一般为1-5
        Return: 返回前k个样本的最大分类标签
        '''
        if self.length <= k:
            label_dict = {}
            # 获取所有label的数量
            for element in self.transfer_list(self.root):
                if element['label'] in label_dict:
                    label_dict[element['label']] += 1
                else:
                    label_dict[element['label']] = 1
            sorted_label = sorted(label_dict.items(), key=lambda item:item[1],reverse=True)  # 给标签排序
            return sorted_label[0][0]
 
        item = np.array(item)
        node = self._find_nearest_neighbour(item)  # 找到最近的那个结点
        if node == None:  # 空树
            return None
        print('靠近点%s最近的叶结点为:%s'%(item, node.item))
        node_list = []
        distance = np.sqrt(sum((item-node.item)**2))  # 测试点与最近点之间的距离
        least_dis = distance
        # 返回上一个父结点，判断以测试点为圆心，distance为半径的圆是否与父结点分隔超平面相交，若相交，则说明父结点的另一个子树可能存在更近的点
        node_list.append([distance, tuple(node.item), node.label[0]])  # 需要将距离与结点一起保存起来
 
        # 若最近的结点不是叶结点，则说明，它还有左子树
        if node.left_child != None:
            left_child = node.left_child
            left_dis = np.sqrt(sum((item-left_child.item)**2))
            if k > len(node_list) or least_dis < least_dis:
                node_list.append([left_dis, tuple(left_child.item), left_child.label[0]])
                node_list.sort()  # 对结点列表按距离排序
                least_dis = node_list[-1][0] if k >= len(node_list) else node_list[k-1][0]
        # 回到父结点
        while True:
            if node == self.root:  # 已经回到kd树的根结点
                break
            parent = node.parent
            # 计算测试点与父结点的距离，与上面距离做比较
            par_dis = np.sqrt(sum((item-parent.item)**2))
            if k >len(node_list) or par_dis < least_dis:  # k大于结点数或者父结点距离小于结点列表中最大的距离
                node_list.append([par_dis, tuple(parent.item) , parent.label[0]])
                node_list.sort()  # 对结点列表按距离排序
                least_dis = node_list[-1][0] if k >= len(node_list) else node_list[k - 1][0]
 
            # 判断父结点的另一个子树与结点列表中最大的距离构成的圆是否有交集
            if k >len(node_list) or abs(item[parent.dim] - parent.item[parent.dim]) < least_dis :  # 说明父结点的另一个子树与圆有交集
                # 说明父结点的另一子树区域与圆有交集
                other_child = parent.left_child if parent.left_child != node else parent.right_child  # 找另一个子树
                # 测试点在该子结点超平面的左侧
                if other_child != None:
                    if item[parent.dim] - parent.item[parent.dim] <= 0:
                        self.left_search(item,other_child,node_list,k)
                    else:
                        self.right_search(item,other_child,node_list,k)  # 测试点在该子结点平面的右侧
 
            node = parent  # 否则继续返回上一层
        # 接下来取出前k个元素中最大的分类标签
        label_dict = {}
        node_list = node_list[:k]
        # 获取所有label的数量
        for element in node_list:
            if element[2] in label_dict:
                label_dict[element[2]] += 1
            else:
                label_dict[element[2]] = 1
        sorted_label = sorted(label_dict.items(), key=lambda item:item[1], reverse=True)  # 给标签排序
        return sorted_label[0][0],node_list
 
    def left_search(self, item, node, nodeList, k):
        '''
        按左中右顺序遍历子树结点，返回结点列表
        Parameter：
            node: 子树结点
            item: 传入的测试样本
            nodeList: 结点列表
            k: 搜索比较的结点数量
        Return: 结点列表
        '''
        nodeList.sort()  # 对结点列表按距离排序
        least_dis = nodeList[-1][0] if k >= len(nodeList) else nodeList[k - 1][0]
        if node.left_child == None and node.right_child == None:  # 叶结点
            dis = np.sqrt(sum((item - node.item) ** 2))
            if k > len(nodeList) or dis < least_dis:
                nodeList.append([dis, tuple(node.item), node.label[0]])
            return
        self.left_search(item, node.left_child, nodeList, k)
        # 每次进行比较前都更新nodelist数据
        nodeList.sort()  # 对结点列表按距离排序
        least_dis = nodeList[-1][0] if k >= len(nodeList) else nodeList[k - 1][0]
        # 比较根结点
        dis = np.sqrt(sum((item-node.item)**2))
        if k > len(nodeList) or dis < least_dis:
            nodeList.append([dis, tuple(node.item), node.label[0]])
        # 右子树
        if k > len(nodeList) or abs(item[node.dim] - node.item[node.dim]) < least_dis: # 需要搜索右子树
            if node.right_child != None:
                self.left_search(item, node.right_child, nodeList, k)
 
        return nodeList
 
    def right_search(self,item, node, nodeList, k):
        '''
        按右中左顺序遍历子树结点
        Parameter：
            item: 测试的样本点
            node: 子树结点
            nodeList: 结点列表
            k: 搜索比较的结点数量
        Return: 结点列表
        '''
        nodeList.sort()  # 对结点列表按距离排序
        least_dis = nodeList[-1][0] if k >= len(nodeList) else nodeList[k - 1][0]
        if node.left_child == None and node.right_child == None:  # 叶结点
            dis = np.sqrt(sum((item - node.item) ** 2))
            if k > len(nodeList) or dis < least_dis:
                nodeList.append([dis, tuple(node.item), node.label[0]])
            return
        if node.right_child != None:
            self.right_search(item, node.right_child, nodeList, k)
 
        nodeList.sort()  # 对结点列表按距离排序
        least_dis = nodeList[-1][0] if k >= len(nodeList) else nodeList[k - 1][0]
        # 比较根结点
        dis = np.sqrt(sum((item - node.item) ** 2))
        if k > len(nodeList) or dis < least_dis:
            nodeList.append([dis, tuple(node.item), node.label[0]])
        # 左子树
        if k > len(nodeList) or abs(item[node.dim] - node.item[node.dim]) < least_dis: # 需要搜索左子树
            self.right_search(item, node.left_child, nodeList, k)
 
        return nodeList

data = np.array([[1, 101], [5, 89], [108, 5], [115, 8], [30, 62], [40, 57]])
labels = ['oarnge', 'orange', 'apple', 'apple', 'banana', 'banana']
x = np.array([101, 20])

group_kd = KDTree(data, labels)

group_kd.knn_algo(item = x)

靠近点[101 20]最近的叶结点为:[108 5]
(‘apple’, [[16.55294535724685, (108, 5), ‘apple’]])

group_kd.knn_algo(item = x, k = 3)

靠近点[101 20]最近的叶结点为:[108 5]
(‘apple’,
[[16.55294535724685, (108, 5), ‘apple’],
[18.439088914585774, (115, 8), ‘apple’],
[71.34423592694787, (40, 57), ‘banana’]])

2.5 sklearn学习k-NN分类

  sklearn.neighbors.KNeighborsClassifier()

  参数列表

参数	参数类型	参数说明
n_neighbors	int（默认5）	k值
weights	str or callable（默认‘uniform’）	实例权重。 ‘uniform’ : 等权重 ‘distance’ : 与距离成反比的权重 [callable] : 一个自定义的以距离为参数并输出等规模权重的函数
algorithm	{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}	实现算法。如果输入的是稀疏数据，那么无论该参数怎样设置，都会强制使用‘brute’方法
leaf_size	int（默认30）	结点的大小，当方法为ball树和kd树时会影响树的构造与搜索速度，用于存储树的内存大小，需要根据实际问题进行判断
p	integer（默认2）	距离度量（$L_p$距离中的$p$）
metric	string or callable（默认‘minkowski’）	使用树算法时用到的距离度量
metric_params	dict（默认None）	度量函数的其他关键字参数
n_jobs	int or None（默认None）	使用的线程，None表示1个线程，-1表示使用所有线程

  方法列表

方法	说明
fit(self, X, y)	训练模型
get_params(self[, deep])	获取模型参数
kneighbors(self[, X, n_neighbors, …])	找出k个近邻
predict(self, X)	预测X的分类
predict_proba(self, X)	预测结果的概率
score(self, X, y[, sample_weight])	测试集准确率

from sklearn.neighbors import KNeighborsClassifier

# 最近邻
clf= KNeighborsClassifier(n_neighbors=1)
clf.fit(data, labels)

clf.predict(x.reshape(1, -1))

array([‘apple’], dtype=’

# k = 3
clf= KNeighborsClassifier(n_neighbors=1)
clf.fit(data, labels)

clf.predict(x.reshape(1, -1))

array([‘apple’], dtype=’

clf.kneighbors([x], n_neighbors = 1)    # 找出距离x最近的点

(array([[16.55294536]]), array([[2]], dtype=int64))

  最近的点是data中的第3个，距离为16.55294536

clf.kneighbors([x], n_neighbors = 3)    # 找出距离x最近的3个点

(array([[16.55294536, 18.43908891, 71.34423593]]),
array([[2, 3, 5]], dtype=int64))

clf.predict_proba([x])

array([[1., 0., 0., 0.]])

3 参考文献

•   《统计学习方法》李航

•   【量化课堂】kd 树算法之详细篇

•   Eric量化交易的知乎

•   qwertWZ的博客

•   wenffe的博客