目标检测2 - SPPNet

SPP-Net

SPP：Spatial Pyramid Pooling（空间金字塔池化）

先看一下R-CNN为什么检测速度这么慢，一张图都需要47s！仔细看下R-CNN框架发现，对图像提完Region Proposal（2000个左右）之后将每个Proposal当成一张图像进行后续处理(CNN提特征+SVM分类)，实际上对一张图像进行了2000次提特征和分类的过程！这2000个Region Proposal不都是图像的一部分吗，那么我们完全可以对图像提一次卷积层特征，然后只需要将Region Proposal在原图的位置映射到卷积层特征图上，这样对于一张图像我们只需要提一次卷积层特征，然后将每个Region Proposal的卷积层特征输入到全连接层做后续操作（对于CNN来说，大部分运算都耗在卷积操作上，这样做可以节省大量时间）。

Q1：原始图片中的RoI如何映射到feature map?

Source: 原始图片中的RoI如何映射到feature map?

对于映射关系，论文中是这么描述的：

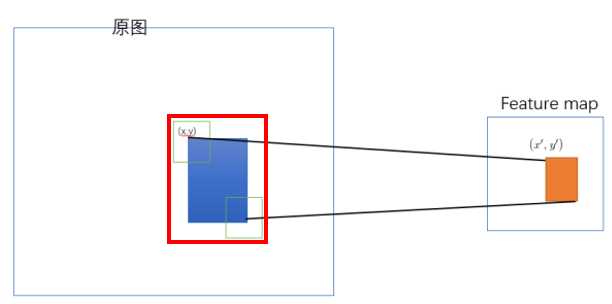
假设 (x′,y′) ( x ′ , y ′ ) 表示特征图上的坐标点，坐标点(x,y)表示原输入图片上的点，那么它们之间有如下转换关系，这种映射关心与网络结构有关： (x,y)=(S∗x′,S∗y′) ( x , y ) = ( S ∗ x ′ , S ∗ y ′ )

反过来，我们希望通过 (x,y) ( x , y ) 坐标求解 (x′,y′) ( x ′ , y ′ ) ，那么计算公式如下：

​ 左上角的点：

x′=⌊x/S⌋+1 x ′ = ⌊ x / S ⌋ + 1

​ 右下角的点：

x′=⌈x/S⌉−1 x ′ = ⌈ x / S ⌉ − 1

其中 S S 就是CNN中所有的strides的乘积，包含了池化、卷积的stride。

比如，对于下图的集中网络结构， S S 的计算如下：

论文中使用的是 ZF-5： S=2∗2∗2∗2=16 S = 2 ∗ 2 ∗ 2 ∗ 2 = 16
​ Overfeat-5/7 : S=2∗3∗2=12 S = 2 ∗ 3 ∗ 2 = 12

然而这个公式怎么来的？ 先来看看感受野的概念。

1. 感受野

卷积神经网络CNN中，某一层输出结果中一个元素所对应的输入层的区域大小，被称作感受野receptive field。

如下图，每一个隐藏层神经元与输入层中 5×5 5 × 5 的神经元有连接。

这个 5×5 5 × 5 的区域就叫做感受野，表示一个隐藏层神经元在输入层的感受区域。这 5×5=25 5 × 5 = 25 个连接对应有25个权重参数 w w ，还有一个全局共用的基值 b b 。

1. 卷积核输出尺寸计算公式

计算卷积核输出size的公式推导：

• 15×15 15 × 15 的输入图片 （ W=15 W = 15 ）
• 5×5 5 × 5 的卷积核 （ K=5 K = 5 )

• 滑动步长（stride）为1 （ S=1 S = 1 ）

  W=15，K=5，S=2 W = 15 ， K = 5 ， S = 2 对应的隐藏神经元是多少？

蓝色表示左上角的 5×5 5 × 5 感受野，绿色是其向右滑动轨迹。

因为 W=15，K=5，S=2 W = 15 ， K = 5 ， S = 2

一次向右滑动对应 6个隐藏神经元 =>

= 5次滑动 + 1个原始感受视野

= 10个绿色区域/步长2 + 1个原始感受视野

= （W−K）/S+1 （ W − K ） / S + 1

得到隐藏层对应的计算公式： 隐藏层边长 =（W−K）/S+1​ = （ W − K ） / S + 1 ​ 。

有时候为了控制输出的隐藏层空间分布会在输入层外围做零填充，假设填充 P个像素， 此时：隐藏层边长 =（W−K+2P）/S+1 = （ W − K + 2 P ） / S + 1 。特别的，当 S=1 S = 1 时， 设置零填充为 P=(K−1)/2 P = ( K − 1 ) / 2 可以保证输入层与输出层有相同的空间分布。

1. 卷积层的输入尺寸计算公式

反过来，卷积层的输入，即前一层在后一层的感受野计算公式为：

• 对于 Convolution/Pooling layer： Wi=Si⋅(Wi+1−1)+Ki−2⋅padding W i = S i ⋅ ( W i + 1 − 1 ) + K i − 2 ⋅ p a d d i n g
• 对于Neuron layer(ReLU/Sigmoid/…) ： Wi=Wi+1 W i = W i + 1

上面只是给出了前一层在后一层的感受野，如何计算最后一层在原始图片上的感受野呢？如下图，如想计算Map 3上某个点在Map 1上的感受野，只需要从后向前级联一下就可以了，即先计算最后一层到倒数第二层的感受野，再计算倒数第二层到倒数第三层的感受野，依次从后往前推导就可以了。

1. 感受野上的坐标映射

通常，我们还需要知道网络里面任意两个feature map之间的坐标映射关系（一般是中心点之间的映射），如下图，我们想得到map 3上的点p3映射回map 2所在的位置p2（橙色框的中心点）

计算公式：

• 对于 Convolution/Pooling layer： pi=Si⋅pi+1+((Ki−1)/2−padding) p i = S i ⋅ p i + 1 + ( ( K i − 1 ) / 2 − p a d d i n g )
• 对于Neuron layer(ReLU/Sigmoid/…) ： pi=pi+1 p i = p i + 1

1. SPP-Net的RoI映射方法

SPP-Net中采用的公式其实就是巧妙的化简一下公式 pi=Si⋅pi+1+((Ki−1)/2−padding) p i = S i ⋅ p i + 1 + ( ( K i − 1 ) / 2 − p a d d i n g ) ，令每一层的padding都为 padding=⌊Ki/2⌋⇒pi=Si⋅pi+1+((Ki−1)/2−⌊ki/2⌋) p a d d i n g = ⌊ K i / 2 ⌋ ⇒ p i = S i ⋅ p i + 1 + ( ( K i − 1 ) / 2 − ⌊ k i / 2 ⌋ )

• 当 Ki K i 为奇数时 ((Ki−1)/2−⌊Ki/2⌋=0 ( ( K i − 1 ) / 2 − ⌊ K i / 2 ⌋ = 0 所以 pi=Si⋅pi+1 p i = S i ⋅ p i + 1
• 当 Ki K i 为偶数时 ((Ki−1)/2−⌊Ki/2⌋=−0.5 ( ( K i − 1 ) / 2 − ⌊ K i / 2 ⌋ = − 0.5 所以 pi=Si⋅pi+1−0.5 p i = S i ⋅ p i + 1 − 0.5
• 而 pi p i 是坐标值，不可能取小数，所以基本上可以认为 pi=Si⋅pi+1 p i = S i ⋅ p i + 1 。公式得到了化简：感受野中心点的坐标 pi p i 只跟前一层 pi+1 p i + 1 和 stride 有关。

SPP-Net的RoI映射实际上就是把原始RoI的左上角和右下角映射到 feature map上的两个对应点。 有了feature map上的两对角点可以确定对应的 feature map 区域(下图中橙色)。

如何映射？

左上角的点 (x,y) ( x , y ) 映射到 feature map上的 (x′,y′) ( x ′ , y ′ ) 使得 (x′,y′) ( x ′ , y ′ ) 在原始图上感受野（上图绿色框）的中心点 与 (x,y) ( x , y ) 尽可能接近。

对应点之间的映射公式是啥？

• 就是前面每层都填充 padding/2 p a d d i n g / 2 得到的简化公式 ： pi=Si⋅pi+1 p i = S i ⋅ p i + 1
• 需要把上面公式进行级联得到 p0=S⋅pi+1 p 0 = S ⋅ p i + 1 其中 (S=∏i0Si) ( S = ∏ 0 i S i )
• 对于feature map上的 (x′,y′) ( x ′ , y ′ ) ，它在原始图的对应点为 (x,y)=(Sx′,Sy′) ( x , y ) = ( S x ′ , S y ′ )
• 论文中的最后做法：把原始图片中的RoI映射为 feature map中的映射区域（上图橙色区域）其中 左上角取： x′=⌊x/S⌋+1,y′=⌊y/S⌋+1 x ′ = ⌊ x / S ⌋ + 1 , y ′ = ⌊ y / S ⌋ + 1 ；右下角的点取： x′=⌈x/S⌉−1,y′=⌈y/S⌉−1 x ′ = ⌈ x / S ⌉ − 1 , y ′ = ⌈ y / S ⌉ − 1 。 下图可见 ⌊x/S⌋+1,⌈x/S⌉−1 ⌊ x / S ⌋ + 1 , ⌈ x / S ⌉ − 1 的作用效果分别是增加和减少。也就是 左上角要向右下偏移，右下角要想要向左上偏移。采取这样的策略可能是因为论文中的映射方法（左上右下映射）会导致feature map上的区域反映射回原始RoI时有多余的区域（下图左边红色框是比蓝色区域大的）

1. 代码模拟感受野计算

#!/usr/bin/env python
# receptiveField.py

net_struct = {'alexnet': {'net':[[11,4,0],[3,2,0],[5,1,2],[3,2,0],[3,1,1],[3,1,1],[3,1,1],[3,2,0]],
                   'name':['conv1','pool1','conv2','pool2','conv3','conv4','conv5','pool5']},
       'vgg16': {'net':[[3,1,1],[3,1,1],[2,2,0],[3,1,1],[3,1,1],[2,2,0],[3,1,1],[3,1,1],[3,1,1],
                        [2,2,0],[3,1,1],[3,1,1],[3,1,1],[2,2,0],[3,1,1],[3,1,1],[3,1,1],[2,2,0]],
                 'name':['conv1_1','conv1_2','pool1','conv2_1','conv2_2','pool2','conv3_1','conv3_2',
                         'conv3_3', 'pool3','conv4_1','conv4_2','conv4_3','pool4','conv5_1','conv5_2','conv5_3','pool5']},
       'zf-5':{'net': [[7,2,3],[3,2,1],[5,2,2],[3,2,1],[3,1,1],[3,1,1],[3,1,1]],
               'name': ['conv1','pool1','conv2','pool2','conv3','conv4','conv5']}}

imsize = 224

# 从前往后计算输出维度
def outFromIn(isz, net, layernum):
    totstride = 1
    insize = isz
    for layer in range(layernum):
        fsize, stride, pad = net[layer]
        outsize = (insize - fsize + 2*pad) / stride + 1
        insize = outsize
        # 注意stride是连乘
        totstride = totstride * stride
    return outsize, totstride

# 从后往前算感受野，返回该层元素在原始图片中的感受野大小
def inFromOut(net, layernum):
    RF = 1
    for layer in reversed(range(layernum)):
        fsize, stride, pad = net[layer]
        RF = ((RF -1)* stride) + fsize
    return RF

if __name__ == '__main__':
    print "layer output sizes given image = %dx%d" % (imsize, imsize)

    for net in net_struct.keys():
        print '************net structrue name is %s**************'% net
        for i in range(len(net_struct[net]['net'])):
            p = outFromIn(imsize,net_struct[net]['net'], i+1)
            rf = inFromOut(net_struct[net]['net'], i+1)
            print "Layer Name = %s, Output size = %3d, Stride = % 3d, RF size = %3d" % (net_struct[net]['name'][i], p[0], p[1], rf)

Q2：为什么FC层需要固定长度输入？

现在的问题是每个Region Proposal的尺度不一样，直接这样输入全连接层肯定是不行的，因为全连接层输入必须是固定的长度。

为什么全连接层需要固定长度的输入？

(有全连接的存在深度网络需要固定输入尺寸)

卷积层的参数和输入大小无关，它仅仅是一个卷积核在图像上滑动，不管输入图像多大都没关系，只是对不同大小的图片卷积出不同大小的特征图，但是全连接层的参数就和输入图像大小有关，因为它要把输入的所有像素点连接起来,需要指定输入层神经元个数和输出层神经元个数，所以需要规定输入的feature的大小。

因此，固定长度的约束仅限于全连接层。以下图为例说明：

作为全连接层，如果输入的x维数不等，那么参数w肯定也会不同，因此，全连接层是必须确定输入，输出个数的。

传统的CNN由于全连接层的存在，限制了输入必须固定大小（比如AlexNet是224x224），所以在实际使用中往往需要对原图片进行crop或者warp的操作：

- crop：截取原图片的一个固定大小的patch
- warp：将原图片的RoI缩放到一个固定大小的patch

无论是crop还是warp，都无法保证在不失真的情况下将图片传入到CNN当中：

• crop：物体可能会产生截断，尤其是长宽比大的图片。
• warp：物体被拉伸，失去“原形”，尤其是长宽比大的图片

而且，从生理学角度出发，人眼看到一个图片时，大脑会首先认为这是一个整体，而不会进行crop和warp，所以更有可能的是，我们的大脑通过搜集一些浅层的信息，在更深层才识别出这些任意形状的目标。

SPP为的就是解决上述的问题，做到的效果为：不管输入的图片是什么尺度，都能够正确的传入网络。

SPP-Net网络结构

左边是训练流程，右边是测试流程，注意SPP-Net是直接用SPP池化层的输出特征作Bounding Box的回归，不像R-CNN是用Conv5的特征。

SPP—空间金字塔池化

把SS提出的区域建议映射到conv5输出的feature map上（如果原图输入是224x224，对于conv5出来后的输出，是13x13x256的），然后把候选区域进行网格划分，3种划分方案[超参] (1×1,2×2,4×4) ( 1 × 1 , 2 × 2 , 4 × 4 ) ，共21个方格，每个方格都会覆盖不同数量的多个像素点，然后每个方格里面都做max pooling，所以每个方格最后输出的都是一个像素的值，因此最后SPP pooling之后输出21段定长的特征——(16+4+1) x 256维（如果原图的输入不是224x224，出来的特征依然是(16+4+1) x 256维），最后(通过1x1的卷积核调整维度后？？)将feature送入FC层，实现了用SPP pooling层替换Conv5层的功能。

SPP-Net训练流程

1. 仍然是取一个pre-train的CNN模型

2. 计算出所有SS区域的SPP pooling层的一维特征

3. 使用步骤2提取的SPP的特征来fine-tune后面的全连接层（FC6，FC7，FC8），全卷积层不参与再训练（可改进）

   与R-CNN的区别：

   • 特征不同：R-CNN是Conv5之后的pooling层的特征送入FC层
   • fine-tune不同：R-CNN是fine-tune所有层，SPP-Net只fine-tune全连接层

4. fine-tune好之后，同R-CNN一样，用FC7层的特征训练SVM分类器

5. 用SPP pooling来训练Bounding Box回归模型

SPP-Net缺点

SPP-Net只解决了R-CNN卷积层计算共享的问题，但是依然存在着其他问题：

• (1) 训练分为多个阶段，步骤繁琐: fine-tune+训练SVM+训练Bounding Box
• (2) SPP-Net在fine-tune网络的时候固定了卷积层，只对全连接层进行微调，而对于一个新的任务，有必要对卷积层也进行fine-tune。（分类的模型提取的特征更注重高层语义，而目标检测任务除了语义信息还需要目标的位置信息）

针对这两个问题，RBG又提出Fast R-CNN, 一个精简而快速的目标检测框架。