拉格朗日插值多项式的原理介绍及其应用

  插值，不论在数学中的数值分析中，还是在我们实际生产生活中，都不难发现它的身影，比如造船业和飞机制造业中的三次样条曲线。那么，什么是插值呢？我们可以先看一下插值的定义，如下：

  （定义）如果对于每个 1≤i≤n,P(xi)=yi 1 ≤ i ≤ n , P ( x i ) = y i ,则称函数 y=P(x) y = P ( x ) 插值数据点 (x1,y1),...,(xn,yn) ( x 1 , y 1 ) , . . . , ( x n , y n ) .

   插值的定义无疑是清楚明了的，而在众多的数学函数中，多项式无疑是最简单，最常见的函数，关于它的理论研究也最为透彻。因此，我们可以不妨先考虑利用多项式来进行插值。那么，这样的多项式是否总是存在呢？答案是肯定的，因为我们有如下定理：

  （多项式插值定理）令 (x1,y1),...,(xn,yn) ( x 1 , y 1 ) , . . . , ( x n , y n ) 是平面中的 n n 个点，各 xi x i 互不相同。则有且仅有一个 n−1 n − 1 次或者更低的多项式 P P 满足 P(xi)=yi,i=1,2,...,n. P ( x i ) = y i , i = 1 , 2 , . . . , n .

  证明:先用归纳法证明存在性，再证明唯一性。
  当 n=1 n = 1 时，常函数(0次) P1(x)=y1 P 1 ( x ) = y 1 即符合要求。假设当 n−1 n − 1 时存在一个次数 ≤n−2 ≤ n − 2 的多项式 Pn−1 P n − 1 ,使得 Pn−1(xi)=yi,i=1,2,...,n−1. P n − 1 ( x i ) = y i , i = 1 , 2 , . . . , n − 1. 则令 Pn(x)=Pn−1(x)+c(x−x1)(x−x2)...(x−xn−1)(x−xn) P n ( x ) = P n − 1 ( x ) + c ( x − x 1 ) ( x − x 2 ) . . . ( x − x n − 1 ) ( x − x n ) ，其中 c c 为待定系数，利用 Pn(xn)=yn P n ( x n ) = y n 即可求出待定系数 c c .此时， Pn(xi)=yi,i=1,2,...,n, P n ( x i ) = y i , i = 1 , 2 , . . . , n , 且 Pn(x) P n ( x ) 的次数 ≤n−1 ≤ n − 1 .这样就证明了存在性。
  其次证明唯一性。假设存在两个这样的多项式，设为 P(x) P ( x ) 和 Q(x) Q ( x ) ，它们次数 ≤n−1 ≤ n − 1 且都插值经过 n n 个点，即 P(xi)=Q(xi)=yi,i=1,2,...,n. P ( x i ) = Q ( x i ) = y i , i = 1 , 2 , . . . , n . 令 H(x)=P(x)−Q(x) H ( x ) = P ( x ) − Q ( x ) , H H 的次数也 ≤n−1 ≤ n − 1 ，且有 n n 个不同的根 x1,x2,...,xn x 1 , x 2 , . . . , x n .因此，由多项式基本定理可知， H(x) H ( x ) 为0多项式，即恒等于0，故有 P(x)=Q(x) P ( x ) = Q ( x ) .这样就证明了存在性。
  证毕。

  有了以上定理，我们可以放心地使用多项式进行插值，同时，通过上述定理，我们可以用归纳法来构造此多项式，但是，这样的方法难免复杂麻烦。于是，天才的法国数学家拉格朗日（Lagrange）创造性地发明了一种实用的插值多项式方法来解决这个问题，那么，他的方法是怎么样的？
  一般来说，如果我们有 n n 个点 (x1,y1),...,(xn,yn) ( x 1 , y 1 ) , . . . , ( x n , y n ) ，各 xi x i 互不相同。对于1到n之间的每个 k k ，定义 n−1 n − 1 次多项式

Lk(x)=(x−x1)..(x−xk−1)(x−xk+1)...(x−xn)(xk−x1)..(xk−xk−1)(xk−xk+1)...(xk−xn) L k ( x ) = ( x − x 1 ) . . ( x − x k − 1 ) ( x − x k + 1 ) . . . ( x − x n ) ( x k − x 1 ) . . ( x k − x k − 1 ) ( x k − x k + 1 ) . . . ( x k − x n )

Lk(x) L k ( x ) 具有有趣的性质： Lk(xk)=1,Lk(xj)=0,j≠k. L k ( x k ) = 1 , L k ( x j ) = 0 , j ≠ k . 然后定义一个 n−1 n − 1 次多项式

Pn−1(x)=y1L1(x)+...+ynLn(x). P n − 1 ( x ) = y 1 L 1 ( x ) + . . . + y n L n ( x ) .

这样的多项式 Pn−1(x) P n − 1 ( x ) 满足 Pn−1(xi)=yi,i=1,2,...,n. P n − 1 ( x i ) = y i , i = 1 , 2 , . . . , n . 这就是著名的拉格朗日插值多项式！
  以上就是拉格朗日插值多项式的理论介绍部分，接下来我们就要用Python中的Sympy模块来实现拉格朗日插值多项式啦~~
  实现拉格朗日插值多项式的Python代码如下：

from sympy import *

def Lagrange_interpolation(keys, values):
    x = symbols('x')
    t = len(keys)
    ploy = []
    for i in range(t):
        lst = ['((x-'+str(_)+')/('+str(keys[i])+'-'+str(_)+'))' for _ in keys if _ != keys[i]]
        item = '*'.join(lst)
        ploy.append(str(values[i])+'*'+item)
    ploy = '+'.join(ploy)

    return factor(expand(ploy))

def main():
    #example 1, interpolate a line 
    x_1 = [1,2]
    y_1 = [3,5]
    if len(x_1) != len(y_1):
        print('The lengths of two list are not equal!')
    else:
        print('Lagrange_interpolation polynomials is:')
        print(Lagrange_interpolation(x_1,y_1))

    #example 2, interpolate a parabola
    x_2 = [0,2,3]
    y_2 = [1,2,4]
    if len(x_2) != len(y_2):
        print('The lengths of two list are not equal!')
    else:
        print('Lagrange_interpolation polynomials is:')
        print(Lagrange_interpolation(x_2,y_2))

    #example 3
    x_3 = [0,1,2,3]
    y_3 = [2,1,0,-1]
    if len(x_3) != len(y_3):
        print('The lengths of two list are not equal!')
    else:
        print('Lagrange_interpolation polynomials is:')
        print(Lagrange_interpolation(x_3,y_3))

main()

函数Lagrange_interpolation()具体实现了拉格朗日插值多项式，参数(keys, values)为list形式的点对，在main()函数中举了三个Lagrange_interpolation()函数的应用实例，一个是插值两个点，即直线，一个是插值三个点，即抛物线，一个是插值四个点，但结果却是一次多项式。该程序的运行结果如下：

  接下来，我们将介绍一个拉格朗日插值多项式的应用，即求

1k+2k+...+xk 1 k + 2 k + . . . + x k

的求和公式，其中 x,k x , k 为正整数。分析如下:
  首先，该求和公式应当是一个至多为k+1次的关于 x x 的多项式。然后，我们可以通过取k+2个不同的点，利用拉格朗日插值多项式的办法来求解，这k+2个不同的点的横坐标可以取 x=1,2,...,k+2 x = 1 , 2 , . . . , k + 2 ,在求出其对应的纵坐标的值。
  以下代码分别求出 k=1,2,...,50 k = 1 , 2 , . . . , 50 的求和公式，并将其插入到Redis中。

from sympy import *
import redis

def Lagrange_interpolation(keys, values):
    x = symbols('x')
    t = len(keys)
    ploy = []
    for i in range(t):
        lst = ['((x-'+str(_)+')/('+str(keys[i])+'-'+str(_)+'))' for _ in keys if _ != keys[i]]
        item = '*'.join(lst)
        ploy.append(str(values[i])+'*'+item)
    ploy = '+'.join(ploy)

    return factor(expand(ploy))

def degree_of_sum(k):
    x_list, y_list = [], []
    degree = k    # degree=k in expression of  1^k+2^k+...+x^{k}
    cul_sum = 0
    for i in range(1,degree+3):
        x_list.append(i)
        cul_sum += i**degree
        y_list.append(cul_sum)
    return Lagrange_interpolation(x_list,y_list)

def main(): 
    r = redis.Redis(host='localhost', port=6379,db=0)
    for k in range(1,51):
        expression = str(degree_of_sum(k))
        r.hset('sum_%s'%k,'degree',str(k))
        r.hset('sum_%s'%k,'expression',expression)
        print('Degree of %d inserted!'%k)

main()

运行以上程序，结果如下：

在Redis中的储存结果如下：



我们可以具体查看当 k=2 k = 2 时的求和公式，如下：



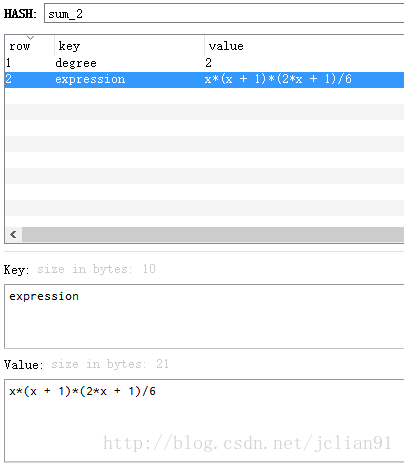
  这样我们就介绍完了一个拉格朗日插值多项式的应用了。看了上面的介绍，聪明又机智的你是否能想到更多拉格朗日插值多项式的应用呢？欢迎大家交流哦~~
  新的一年，新的气象，就从这一篇开始~~

注意：本人现已开通两个微信公众号： 用Python做数学（微信号为：python_math）以及轻松学会Python爬虫（微信号为：easy_web_scrape）， 欢迎大家关注哦~~