faster-rcnn 之 RPN网络的结构解析
【说明】:欢迎加入:faster-rcnn 交流群 238138700,我想很多人在看faster-rcnn的时候,都会被RPN的网络结构和连接方式纠结,作者在文中说的不是很清晰,这里给出解析;
【首先】:大家应该要了解卷积神经网络的连接方式,卷积核的维度,反向传播时是如何灵活的插入一层;这里我推荐一份资料,真是写的非常清晰,就是MatConvet的用户手册,这个框架底层借用的是caffe的算法,所以他们的数据结构,网络层的连接方式都是一样的;建议读者看看,很快的;
下载链接:点击打开链接
【前面5层】:作者RPN网络前面的5层借用的是ZF网络,这个网络的结构图我截个图放在下面,并分析下为什么是这样子的;
1、首先,输入图片大小是 224*224*3(这个3是三个通道,也就是RGB三种)
2、然后第一层的卷积核维度是 7*7*3*96 (所以大家要认识到卷积核都是4维的,在caffe的矩阵计算中都是这么实现的);
3、所以conv1得到的结果是110*110*96 (这个110来自于 (224-7+pad)/2 +1 ,这个pad是我们常说的填充,也就是在图片的周围补充像素,这样做的目的是为了能够整除,除以2是因为2是图中的stride, 这个计算方法在上面建议的文档中有说明与推导的);
4、然后就是做一次池化,得到pool1, 池化的核的大小是3*3,所以池化后图片的维度是55*55*96 ( (110-3+pad)/2 +1 =55 );
5、然后接着就是再一次卷积,这次的卷积核的维度是5*5*96*256 ,得到conv2:26*26*256;
6、后面就是类似的过程了,我就不详细一步步算了,要注意有些地方除法除不尽,作者是做了填充了,在caffe的prototxt文件中,可以看到每一层的pad的大小;
7、最后作者取的是conv5的输出,也就是13*13*256送给RPN网络的;
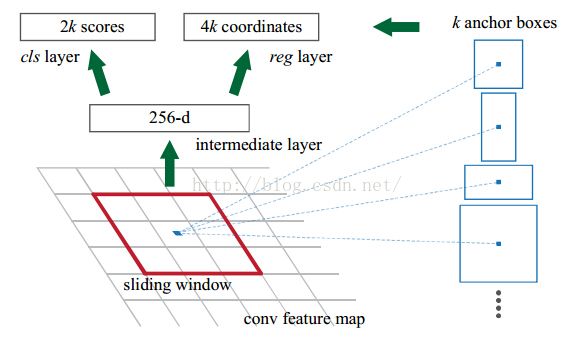
【RPN部分】:然后,我们看看RPN部分的结构:
1、前面我们指出,这个conv feature map的维度是13*13*256的;
2、作者在文章中指出,sliding window的大小是3*3的,那么如何得到这个256-d的向量呢? 这个很简单了,我们只需要一个3*3*256*256这样的一个4维的卷积核,就可以将每一个3*3的sliding window 卷积成一个256维的向量;
这里读者要注意啊,作者这里画的示意图 仅仅是 针对一个sliding window的;在实际实现中,我们有很多个sliding window,所以得到的并不是一维的256-d向量,实际上还是一个3维的矩阵数据结构;可能写成for循环做sliding window大家会比较清楚,当用矩阵运算的时候,会稍微绕些;
3、然后就是k=9,所以cls layer就是18个输出节点了,那么在256-d和cls layer之间使用一个1*1*256*18的卷积核,就可以得到cls layer,当然这个1*1*256*18的卷积核就是大家平常理解的全连接;所以全连接只是卷积操作的一种特殊情况(当卷积核的大小与图片大小相同的时候,其实所谓的卷积就是全连接了);
4、reg layer也是一样了,reg layer的输出是36个,所以对应的卷积核是1*1*256*36,这样就可以得到reg layer的输出了;
5、然后cls layer 和reg layer后面都会接到自己的损失函数上,给出损失函数的值,同时会根据求导的结果,给出反向传播的数据,这个过程读者还是参考上面给的文档,写的挺清楚的;
【作者关于RPN网络的具体定义】:这个作者是放在./models/pascal_voc/ZF/faster_rcnn_alt_opt/stage1_rpn_train.pt 文件中的;
我把这个文件拿出来给注释下:
name: "ZF"
layer {
name: 'input-data' #这一层就是最开始数据输入
type: 'Python'
top: 'data' # top表示该层的输出,所以可以看到这一层输出三组数据,data,真值框gt_boxes,和相关信息im_info
top: 'im_info' # 这些都是存储在矩阵中的
top: 'gt_boxes'
python_param {
module: 'roi_data_layer.layer'
layer: 'RoIDataLayer'
param_str: "'num_classes': 21"
}
}
#========= conv1-conv5 ============
layer {
name: "conv1"
type: "Convolution"
bottom: "data" # 输入data
top: "conv1" # 输出conv1,这里conv1就代表了这一层输出数据的名称,存储在对应的矩阵中
param { lr_mult: 1.0 }
param { lr_mult: 2.0 }
convolution_param {
num_output: 96
kernel_size: 7
pad: 3 # 这里可以看到卷积1层 填充了3个像素
stride: 2
}
}
layer {
name: "relu1"
type: "ReLU"
bottom: "conv1"
top: "conv1"
}
layer {
name: "norm1"
type: "LRN"
bottom: "conv1"
top: "norm1" # 做归一化操作,通俗点说就是做个除法
lrn_param {
local_size: 3
alpha: 0.00005
beta: 0.75
norm_region: WITHIN_CHANNEL
engine: CAFFE
}
}
layer {
name: "pool1"
type: "Pooling"
bottom: "norm1"
top: "pool1"
pooling_param {
kernel_size: 3
stride: 2
pad: 1 # 池化的时候,又做了填充
pool: MAX
}
}
layer {
name: "conv2"
type: "Convolution"
bottom: "pool1"
top: "conv2"
param { lr_mult: 1.0 }
param { lr_mult: 2.0 }
convolution_param {
num_output: 256
kernel_size: 5
pad: 2
stride: 2
}
}
layer {
name: "relu2"
type: "ReLU"
bottom: "conv2"
top: "conv2"
}
layer {
name: "norm2"
type: "LRN"
bottom: "conv2"
top: "norm2"
lrn_param {
local_size: 3
alpha: 0.00005
beta: 0.75
norm_region: WITHIN_CHANNEL
engine: CAFFE
}
}
layer {
name: "pool2"
type: "Pooling"
bottom: "norm2"
top: "pool2"
pooling_param {
kernel_size: 3
stride: 2
pad: 1
pool: MAX
}
}
layer {
name: "conv3"
type: "Convolution"
bottom: "pool2"
top: "conv3"
param { lr_mult: 1.0 }
param { lr_mult: 2.0 }
convolution_param {
num_output: 384
kernel_size: 3
pad: 1
stride: 1
}
}
layer {
name: "relu3"
type: "ReLU"
bottom: "conv3"
top: "conv3"
}
layer {
name: "conv4"
type: "Convolution"
bottom: "conv3"
top: "conv4"
param { lr_mult: 1.0 }
param { lr_mult: 2.0 }
convolution_param {
num_output: 384
kernel_size: 3
pad: 1
stride: 1
}
}
layer {
name: "relu4"
type: "ReLU"
bottom: "conv4"
top: "conv4"
}
layer {
name: "conv5"
type: "Convolution"
bottom: "conv4"
top: "conv5"
param { lr_mult: 1.0 }
param { lr_mult: 2.0 }
convolution_param {
num_output: 256
kernel_size: 3
pad: 1
stride: 1
}
}
layer {
name: "relu5"
type: "ReLU"
bottom: "conv5"
top: "conv5"
}
#========= RPN ============
# 到我们的RPN网络部分了,前面的都是共享的5层卷积层的部分
layer {
name: "rpn_conv1"
type: "Convolution"
bottom: "conv5"
top: "rpn_conv1"
param { lr_mult: 1.0 }
param { lr_mult: 2.0 }
convolution_param {
num_output: 256
kernel_size: 3 pad: 1 stride: 1 #这里作者把每个滑窗3*3,通过3*3*256*256的卷积核输出256维,完整的输出其实是12*12*256,
weight_filler { type: "gaussian" std: 0.01 }
bias_filler { type: "constant" value: 0 }
}
}
layer {
name: "rpn_relu1"
type: "ReLU"
bottom: "rpn_conv1"
top: "rpn_conv1"
}
layer {
name: "rpn_cls_score"
type: "Convolution"
bottom: "rpn_conv1"
top: "rpn_cls_score"
param { lr_mult: 1.0 }
param { lr_mult: 2.0 }
convolution_param {
num_output: 18 # 2(bg/fg) * 9(anchors)
kernel_size: 1 pad: 0 stride: 1 #这里看的很清楚,作者通过1*1*256*18的卷积核,将前面的256维数据转换成了18个输出
weight_filler { type: "gaussian" std: 0.01 }
bias_filler { type: "constant" value: 0 }
}
}
layer {
name: "rpn_bbox_pred"
type: "Convolution"
bottom: "rpn_conv1"
top: "rpn_bbox_pred"
param { lr_mult: 1.0 }
param { lr_mult: 2.0 }
convolution_param {
num_output: 36 # 4 * 9(anchors)
kernel_size: 1 pad: 0 stride: 1 #这里看的很清楚,作者通过1*1*256*36的卷积核,将前面的256维数据转换成了36个输出
weight_filler { type: "gaussian" std: 0.01 }
bias_filler { type: "constant" value: 0 }
}
}
layer {
bottom: "rpn_cls_score"
top: "rpn_cls_score_reshape" # 我们之前说过,其实这一层是12*12*256的,所以后面我们要送给损失函数,需要将这个矩阵reshape一下,我们需要的是144个滑窗,每个对应的256的向量
name: "rpn_cls_score_reshape"
type: "Reshape"
reshape_param { shape { dim: 0 dim: 2 dim: -1 dim: 0 } }
}
layer {
name: 'rpn-data'
type: 'Python'
bottom: 'rpn_cls_score'
bottom: 'gt_boxes'
bottom: 'im_info'
bottom: 'data'
top: 'rpn_labels'
top: 'rpn_bbox_targets'
top: 'rpn_bbox_inside_weights'
top: 'rpn_bbox_outside_weights'
python_param {
module: 'rpn.anchor_target_layer'
layer: 'AnchorTargetLayer'
param_str: "'feat_stride': 16"
}
}
layer {
name: "rpn_loss_cls"
type: "SoftmaxWithLoss" # 很明显这里是计算softmax的损失,输入labels和cls layer的18个输出(中间reshape了一下),输出损失函数的具体值
bottom: "rpn_cls_score_reshape"
bottom: "rpn_labels"
propagate_down: 1
propagate_down: 0
top: "rpn_cls_loss"
loss_weight: 1
loss_param {
ignore_label: -1
normalize: true
}
}
layer {
name: "rpn_loss_bbox"
type: "SmoothL1Loss" # 这里计算的框回归损失函数具体的值
bottom: "rpn_bbox_pred"
bottom: "rpn_bbox_targets"
bottom: "rpn_bbox_inside_weights"
bottom: "rpn_bbox_outside_weights"
top: "rpn_loss_bbox"
loss_weight: 1
smooth_l1_loss_param { sigma: 3.0 }
}
#========= RCNN ============
# Dummy layers so that initial parameters are saved into the output net
layer {
name: "dummy_roi_pool_conv5"
type: "DummyData"
top: "dummy_roi_pool_conv5"
dummy_data_param {
shape { dim: 1 dim: 9216 }
data_filler { type: "gaussian" std: 0.01 }
}
}
layer {
name: "fc6"
type: "InnerProduct"
bottom: "dummy_roi_pool_conv5"
top: "fc6"
param { lr_mult: 0 decay_mult: 0 }
param { lr_mult: 0 decay_mult: 0 }
inner_product_param {
num_output: 4096
}
}
layer {
name: "relu6"
type: "ReLU"
bottom: "fc6"
top: "fc6"
}
layer {
name: "fc7"
type: "InnerProduct"
bottom: "fc6"
top: "fc7"
param { lr_mult: 0 decay_mult: 0 }
param { lr_mult: 0 decay_mult: 0 }
inner_product_param {
num_output: 4096
}
}
layer {
name: "silence_fc7"
type: "Silence"
bottom: "fc7"
}
ps:等源码看完之后,我再注释得更详细些;
作者:香蕉麦乐迪--sloanqin-覃元元