玩转算法之面试第九章-动态规划
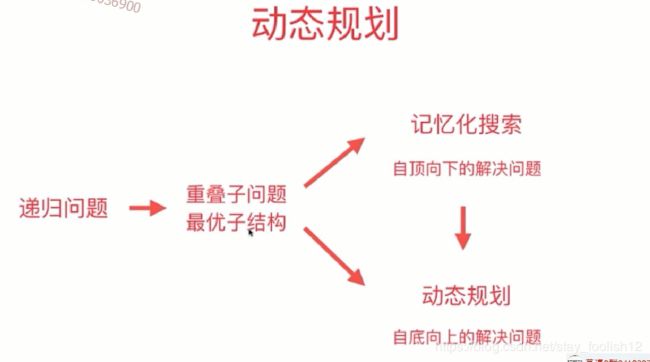
动态规划：
9-12
斐波那契数列
对重复计算，进行优化，进行记忆化搜索
假设基本的问题已经被解决，依次内推。
动态规划：将原问题拆解成若干个子问题，同时保存子问题的答案，使得每个子问题只求解一次，最终获得原问题的答案。
leetcode 20
自顶向下分析可得：
f（n）=f（n-1）+f（n-2）
将上述函数修改动态规划写法：
部分代码如下：
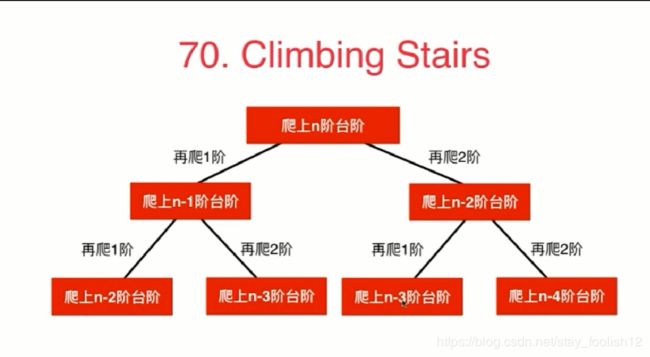
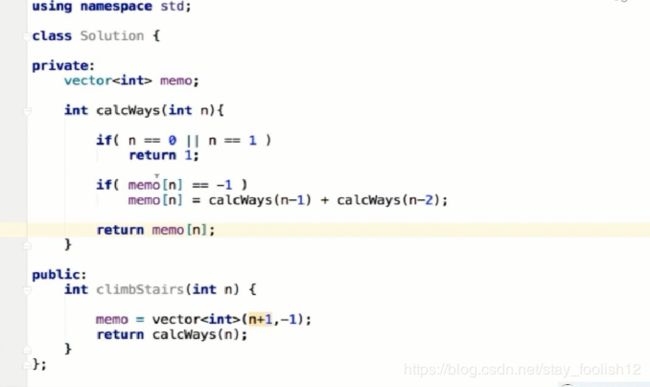
在这里插入代码片
//跳台阶
#include
#include
using namespace std;
class Solution{
private:
vector memo;
int calcWays(int n){
if(n==0 || n==1)
return 1;
//if(n==1)
//return 1;
//if(n==2)
//return 2;
if(memo[n]==-1)
memo[n]=calcWays(n-1)+calcWays(n-2);
retrun memo[n];
}
public:
int climbStairs(int n){
memo=vector(n+1,-1);
return calcWays(n);
}
};
int main(){
return 0;
}
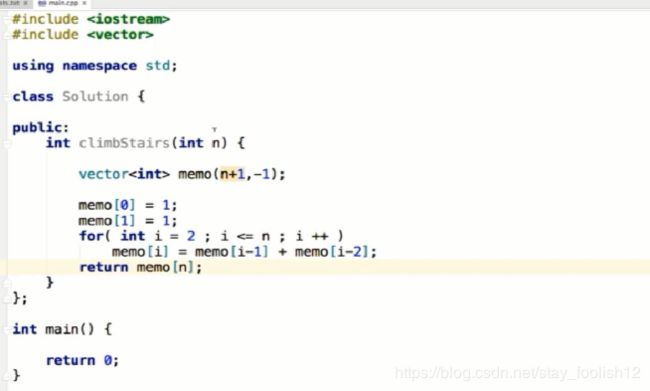
//调台阶修改成动态规划
#include
#include
using namespace std;
class Solution{
public:
int climbStairs(int n){
vector memo(n+1,-1);
memo[0]=1;
memo[1]=1;
for(int i=2;i leetcode：120
leetcode 64
每一步只能左移或者下移
9-3
leetcode 343整数分割
最优子结构： 通过求子问题的最优解，可以获得原问题的最优解
部分代码如下：
在这里插入代码片
//整数分割的问题
#include
#include
#include
//记忆化搜索的关键是对访问过的值进行记录，即用memo数组对结果进行保存
using namespace std;
class Solution{
private:
int max3(int a,int b,int c){
return max(a,max(b,c));
}
//将n进行分割，至少分割成两部分，可以获得的最大乘积
int breakInteger(int n){
if(n==1)
return 1;
if(memo[n]!=-1)
return memo[n];
int res=-1;
for(int i=1; i<=n-1; i++)
//i+(n-i)
res=max3(res,i*(n-i),i*breakInteger(n-i));
memo[n]=res;
return res;
}
public:
int integerBreak(int n){
assert(n>=2);
memo=vector(n+1,-1);
return breakInteger(n);
}
};
int main() {
return 0;
}
修改成动态规划的问题
部分代码如下：
//整数分割的问题
#include
#include
#include
//记忆化搜索的关键是对访问过的值进行记录，即用memo数组对结果进行保存
using namespace std;
class Solution{
private:
int max3(int a,int b,int c){
return max(a,max(b,c));
}
}
public:
int integerBreak(int n){
assert(n>=2);
//将memo[i]进行分割，至少分割成两部分，可以获得的最大乘积
vector memo(n+1,-1);
memo[1]=1;
for(int i=1;i leetcode 279完全平方数
leetcode 91：解析方式
leetcode 62 不同路径
leetcode 63 机器人 障碍物
9-4
leetcode 198 打家劫舍
房子不相邻
价值最大
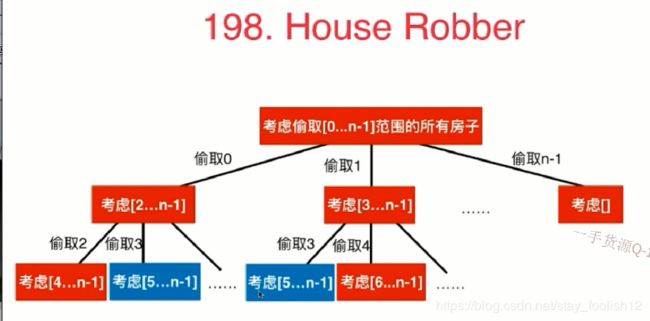
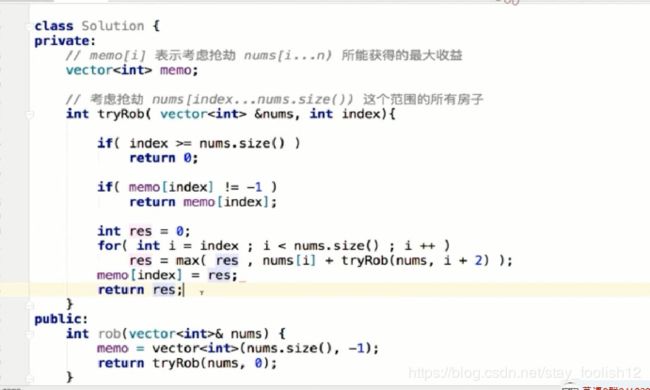
在这里插入代码片
//打家劫舍
#include
#include
using namespace std;
class Solution{
private:
//memo[i]表示抢劫nums[i...n]所能获得的最大收益
vector memo;
//考虑抢劫nums[index...nums.size())这个范围的所有房子
int tryRob(vector &nums,int index){
if(index>=nums.size())
return 0;
if(memo[index]!=-1)
return memo[index];
int res=0;
for(i=index;i& nums){
memo=vector(nums.size(),-1);
return tryRob(nums,0);
}
};
int main(){
return 0;
}
修改成动态规划问题
在这里插入代码片
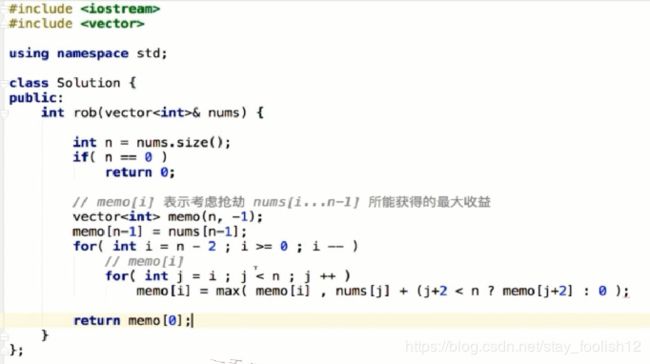
//打家劫舍动态规划
#include
#include
using namespace std;
class Solution{
private:
public:
int rob(vector& nums){
int n=nums.size();
if(n==0)
return 0;
//memo[i]表示抢劫nums[i...n-1]所能获得的最大收益
vectormemo(n,-1);
memo[n-1]=nums[n-1];
for(int i=n-2;i>=0;i--)
//memo[i]
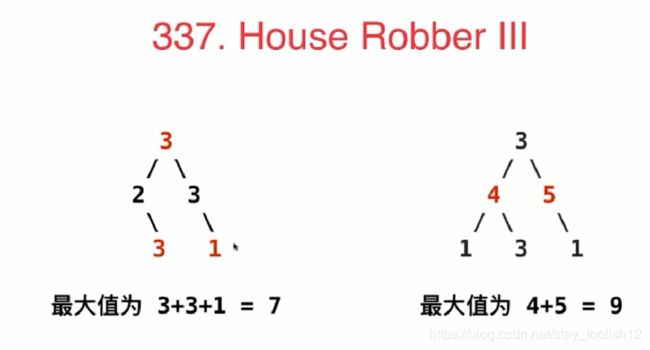
for(int j=i; j leetcode 213
leetcode 337
leetcode 309
设计一个自动交易算法
9-5 0-1背包问题
贪心算法？优先放入平均价值最高的物品？
最优解应该为22>16贪心算法
在这里插入代码片
//0-1背包问题
#include
#include
using namespace std;
class knapsack01{
private:
vector> memo;
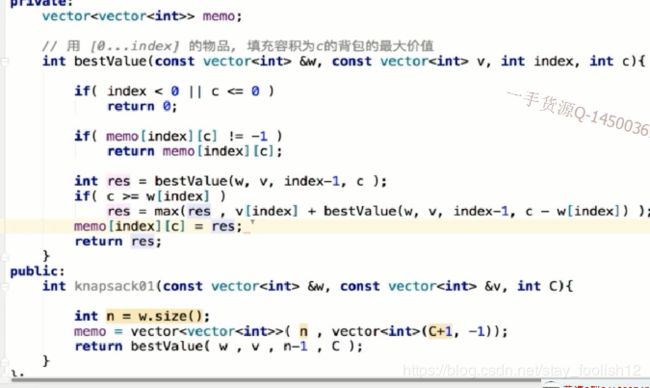
//用[0...index]的物品，填充容积为c的背包的最大价值
int bestValue(const vector &w, const vector v, int index, int c){
if(index<0 || c<=0)
return 0;
if(memo[index][c]!=-1)
return memo[index][c];
int res=bestValue(w,v,index-1,c);
if(c>=w[index])
res=max(v[index]+bestValue(w,v,index-1,c-w[index]);
memo[index][c]=res;
return res;
}
public:
int knapsack01(const vector &w, const vector &v, int C){
int n=w.size();
memo=vector>(n,vector(C+1,-1));
return bestValve(w,v,n-1,c);
}
};
int main(){
return 0;
}
如何自顶向下解决该问题
横轴为容量，纵轴为背包id
在这里插入代码片
//0-1背包动态规划问题
#include
#include
using namespace std;
class knapsack01{
public:
int knapsack01(const vector &w, const vector &v, int C){
assert(w.size()==v.size());
int n=w.size();
if(n==0 || C==0)
return 0;
vector> memo(n,vector(C+1,-1));
for(int j=0; j<=C; j++)
memo[0][j]=(j>=w[0] ? v[0] : 0);
for(int i=1; i=w[i])
memo[i][j]=max(memo[i][j],v[i]+memo[i-1][j-w[i]])
}
return memo[n-1][C];
}
};
int main(){
return 0;
}
9-6
0-1背包问题的优化
在这里插入代码片
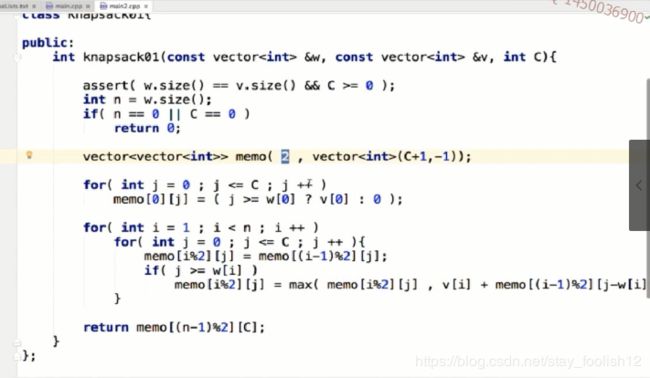
//0-1背包动态空间复杂度的优化问题
#include
#include
using namespace std;
class knapsack01{
public:
int knapsack01(const vector &w, const vector &v, int C){
assert(w.size()==v.size());
int n=w.size();
if(n==0 || C==0)
return 0;
vector> memo(2,vector(C+1,-1));//将n改为2
for(int j=0; j<=C; j++)
memo[0][j]=(j>=w[0] ? v[0] : 0);
for(int i=1; i=w[i])
memo[i%2][j]=max(memo[i][j],v[i]+memo[(i-1)%2][j-w[i]])
}
return memo[(i-1)%2][C];
}
};
int main(){
return 0;
}
只考虑0的情况状态
如果现在将1纳入背包的状态，从右向左更新状态，比如5，在3的基础上加1的为16，大于6则更新为16.依次类推，更新所有状态。
在这里插入代码片
//0-1背包动态空间复杂度的继续优化问题
#include
#include
using namespace std;
class knapsack01{
public:
int knapsack01(const vector &w, const vector &v, int C){
assert(w.size()==v.size());
int n=w.size();
if(n==0|| C==0)
return 0;
vector memo(C+1,-1);//将n*c改为1*c
for(int j=0; j<=C; j++)
memo[j]=(j>=w[0] ? v[0] : 0);
for(int i=1; i=w[i]; j--){
//0-i这些物品，背包为j
//从n*c的复杂度变成了2*c的复杂度
memo[j]=max(memo[j],v[i]+memo[j-w[i]]);
}
return memo[C];
}
};
int main(){
return 0;
}
0-1背包问题的变种
1 完全背包问题：每个物品可以无限使用
定容量，每个物品使用功能次数有最大值，对每个物品可以考虑使用二进制进行表示
2 多重背包问题：每个物品不止一个，有num[i]个
3 多维费用背包问题：要考虑物品的体积和重量两个维度？
物品间加入更多约束
物品间可以互相排斥；也可以互相依赖
9-7
leetcode 416
//数组分割成相等的两部分，其实也是变相的0-1背包问题，容量为sum/2
#include
#include
using namespace std;
class Solution{
private:
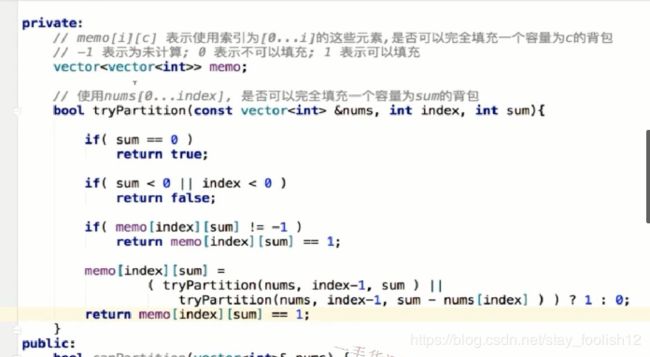
//memo[i][c]表示是否使用索引[0...i]的这些元素，是否可以完全填充一个容量为c的背包
//-1 表示未计算，0表示不可以填充，1表示可以填充
vector> memo;
//s使用nums[0...index],是否可以完全填充一个容量为sum的背包
bool tryPartition(const vector &nums, int index, int sum){
if(sum==0)
return true;
if(sum<0 || index<0)
return false;
if(memo[index][sum] !=-1)
return memo[index][sum]==1;
memo[index][sum]=(tryPartition(nums,index-1,sum)
|| tryPartition(nums,index-1,sum-nums[index])) ? 1 : 0 ;
return memo[index][sum]==1;//等于1，则为true，反之为false
}
public:
bool canPartition(vector& nums){
int sum =0;
for(int i=0;i0);
sum+=nums[i];
}
if(summ%2 !=0)
return false;
memo=vector>(nums.size(),vector(sum/2));
//表示memo存储了nums.size()这么多行，每一行是一个向量，并且每一行有sum/2这么多元素
tryPartition(nums,nums.size()-1,sum/2);
}
};
int main(){
return 0;
}
转换成动态规划问题
//数组分割成相等的两部分，其实也是变相的0-1背包问题，容量为sum/2
//转换成动态规划问题
#include
#include
#include
using namespace std;
class Solution{
public:
bool canPartition(vector& nums){
int sum =0;
for(int i=0;i0);
sum+=nums[i];
}
if(summ%2 !=0)
return false;
int n=nums.size();
int C=sum/2;
vector memo(C+1,false);
for(int i=-; i<=C;i++){
memo[i]=(nums[0]==i);
for(int i=1; i=nums[i];j--)
memo[j]=memo[j] || memo[j-nums[i]];
return memo[C];
}
}
};
int main(){
return 0;
}
练习： leetcode 322 硬币换现
leetcode 377 数组凑数
leetcode 474 01串
leetcode 139 字符串连接
leetcode 494 给定整数sum
9-8 9
leetcode 300最长上升子序列的长度
边界情况：当两个元素是否相等的情况，这种情况他是否算在里面
初始化为1
根据状态方程更新各个长度值
最后扫描一组的最大值
//最长上升子序列 //o(n^2)
#include
#include
using namespace std;
class Solution{
public:
int lengthOfLIS(vector& nums){
if(nums.size()==0)
return 0;
//memo[i] 表示nums[i]为结尾的最长上升子序列的长度
vector memo(nums.size(), 1)；
for(int i=1; i 思考
leetcode： 376 升降轮流序列
最长公共子序列
longgest common sequence
图论中最短路径
