统计学习方法笔记二-----感知机算法(PLA)代码实现
代码实现
上一节,我们介绍了感知机算法(PLA)的理论知识,本节,我们主要讲解一下利用Python实现感知机算法。
算法一
首选,我们利用Python,按照上一节介绍的感知机算法基本思想,实现感知算法的原始形式和对偶形式。
#利用Python实现感知机算法的原始形式
# -*- encoding:utf-8 -*-
"""
Created on 2017.6.7
@author: Ada
"""
import numpy as np
import matplotlib.pyplot as plt
#1、创建数据集
def createdata():
samples=np.array([[3,-3],[4,-3],[1,1],[1,2]])
labels=[-1,-1,1,1]
return samples,labels
#训练感知机模型
class Perceptron:
def __init__(self,x,y,a=1):
self.x=x
self.y=y
self.w=np.zeros((x.shape[1],1))#初始化权重,w1,w2均为0
self.b=0
self.a=1#学习率
self.numsamples=self.x.shape[0]
self.numfeatures=self.x.shape[1]
def sign(self,w,b,x):
y=np.dot(x,w)+b
return int(y)
def update(self,label_i,data_i):
tmp=label_i*self.a*data_i
tmp=tmp.reshape(self.w.shape)
#更新w和b
self.w=tmp+self.w
self.b=self.b+label_i*self.a
def train(self):
isFind=False
while not isFind:
count=0
for i in range(self.numsamples):
tmpY=self.sign(self.w,self.b,self.x[i,:])
if tmpY*self.y[i]<=0:#如果是一个误分类实例点
print '误分类点为:',self.x[i,:],'此时的w和b为:',self.w,self.b
count+=1
self.update(self.y[i],self.x[i,:])
if count==0:
print '最终训练得到的w和b为:',self.w,self.b
isFind=True
return self.w,self.b
#画图描绘
class Picture:
def __init__(self,data,w,b):
self.b=b
self.w=w
plt.figure(1)
plt.title('Perceptron Learning Algorithm',size=14)
plt.xlabel('x0-axis',size=14)
plt.ylabel('x1-axis',size=14)
xData=np.linspace(0,5,100)
yData=self.expression(xData)
plt.plot(xData,yData,color='r',label='sample data')
plt.scatter(data[0][0],data[0][1],s=50)
plt.scatter(data[1][0],data[1][1],s=50)
plt.scatter(data[2][0],data[2][1],s=50,marker='x')
plt.scatter(data[3][0],data[3][1],s=50,marker='x')
plt.savefig('2d.png',dpi=75)
def expression(self,x):
y=(-self.b-self.w[0]*x)/self.w[1]#注意在此,把x0,x1当做两个坐标轴,把x1当做自变量,x2为因变量
return y
def Show(self):
plt.show()
if __name__ == '__main__':
samples,labels=createdata()
myperceptron=Perceptron(x=samples,y=labels)
weights,bias=myperceptron.train()
Picture=Picture(samples,weights,bias)
Picture.Show()
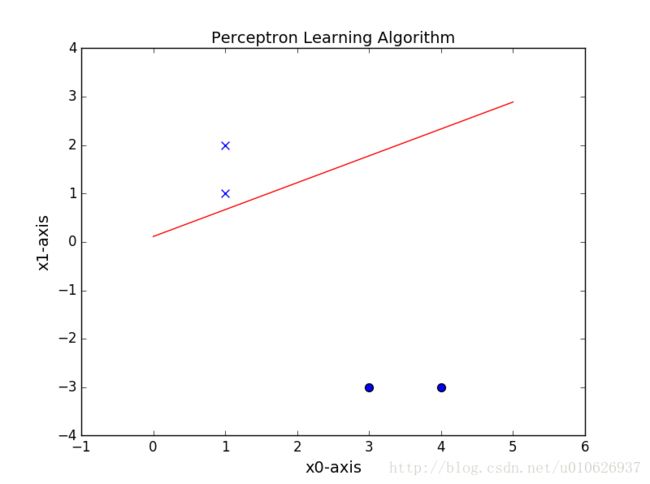
实验结果:
误分类点为: [ 3 -3] 此时的w和b为: [[ 0.]
[ 0.]] 0
误分类点为: [1 1] 此时的w和b为: [[-3.]
[ 3.]] -1
最终训练得到的w和b为: [[-2.]
[ 4.]] 0
#利用Python实现感知机算法的对偶形式
# -*- encoding:utf-8 -*-
"""
Created on 2017.6.7
@author: Ada
"""
import numpy as np
import matplotlib.pyplot as plt
#1、创建数据集
def createdata():
samples=np.array([[3,-3],[4,-3],[1,1],[1,2]])
labels=np.array([-1,-1,1,1])
return samples,labels
#训练感知机模型
class Perceptron:
def __init__(self,x,y,a=1):
self.x=x
self.y=y
self.w=np.zeros((1,x.shape[0]))
self.b=0
self.a=1#学习率
self.numsamples=self.x.shape[0]
self.numfeatures=self.x.shape[1]
self.gMatrix=self.cal_gram(self.x)
def cal_gram(self,x):
gMatrix=np.zeros((self.numsamples,self.numsamples))
for i in xrange(self.numsamples):
for j in xrange(self.numsamples):
gMatrix[i][j]=np.dot(self.x[i,:],self.x[j,:])
return gMatrix
def sign(self,w,b,key):
y=np.dot(w*self.y,self.gMatrix[:,key])+b
return int(y)
def update(self,i):
self.w[i,]=self.w[i,]+self.a
self.b=self.b+self.y[i]*self.a
def cal_w(self):
w=np.dot(self.w*self.y,self.x)
return w
def train(self):
isFind=False
while not isFind:
count=0
for i in range(self.numsamples):
tmpY=self.sign(self.w,self.b,i)
if tmpY*self.y[i]<=0:#如果是一个误分类实例点
print '误分类点为:',self.x[i,:],'此时的w和b为:',self.cal_w(),',',self.b
count+=1
self.update(i)
if count==0:
print '最终训练得到的w和b为:',self.cal_w(),',',self.b
isFind=True
weights=self.cal_w()
return weights,self.b
#画图描绘
class Picture:
def __init__(self,data,w,b):
self.b=b
self.w=w
plt.figure(1)
plt.title('Perceptron Learning Algorithm',size=14)
plt.xlabel('x0-axis',size=14)
plt.ylabel('x1-axis',size=14)
xData=np.linspace(0,5,100)
yData=self.expression(xData)
plt.plot(xData,yData,color='r',label='sample data')
plt.scatter(data[0][0],data[0][1],s=50)
plt.scatter(data[1][0],data[1][1],s=50)
plt.scatter(data[2][0],data[2][1],s=50,marker='x')
plt.scatter(data[3][0],data[3][1],s=50,marker='x')
plt.savefig('2d.png',dpi=75)
def expression(self,x):
y=(-self.b-self.w[:,0]*x)/self.w[:,1]
return y
def Show(self):
plt.show()
if __name__ == '__main__':
samples,labels=createdata()
myperceptron=Perceptron(x=samples,y=labels)
weights,bias=myperceptron.train()
Picture=Picture(samples,weights,bias)
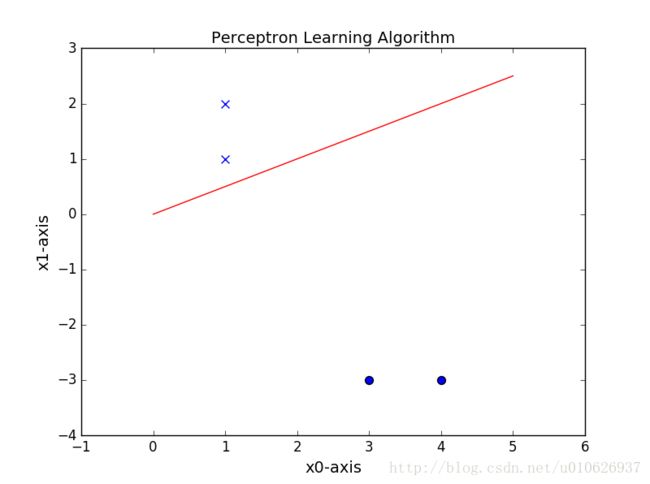
Picture.Show()实验结果:
误分类点为: [ 3 -3] 此时的w和b为: [[ 0. 0.]] , 0
最终训练得到的w和b为: [[-5. 9.]] , -1
通过以上实验结果可以看出,两种方法的结果是不同的,一方面,是由于两种优化方法不同;二是,因为在选择实例点的顺序上有关系。但是无论用哪种方法,都可以找到一条直线,把数据完全分开。实际上,就算使用同一算法,如果改变初始值w0,b0,或者改变选择实例点的顺序,也可以使得结果不同。
算法二
Python的机器学习包sklearn中也包含了感知机学习算法,我们可以直接调用,因为感知机算法属于线性模型,所以从sklearn.linear_model中import下面给出例子。
# -*- encoding:utf-8 -*-
"""
利用sklearn中的感知机学习算法进行实验
Created on 2017.6.7
@author: Ada
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Perceptron
#创建数据,直接定义数据列表
def creatdata1():
samples=np.array([[3,-3],[4,-3],[1,1],[1,2]])
labels=np.array([-1,-1,1,1])
return samples,labels
def MyPerceptron(samples,labels):
#定义感知机
clf=Perceptron(fit_intercept=True,n_iter=30,shuffle=False)
#训练感知机
clf.fit(samples,labels)
#得到权重矩阵
weigths=clf.coef_
#得到截距bisa
bias=clf.intercept_
return weigths,bias
#画图描绘
class Picture:
def __init__(self,data,w,b):
self.b=b
self.w=w
plt.figure(1)
plt.title('Perceptron Learning Algorithm',size=14)
plt.xlabel('x0-axis',size=14)
plt.ylabel('x1-axis',size=14)
xData=np.linspace(0,5,100)
yData=self.expression(xData)
plt.plot(xData,yData,color='r',label='sample data')
plt.scatter(data[0][0],data[0][1],s=50)
plt.scatter(data[1][0],data[1][1],s=50)
plt.scatter(data[2][0],data[2][1],s=50,marker='x')
plt.scatter(data[3][0],data[3][1],s=50,marker='x')
plt.savefig('3d.png',dpi=75)
def expression(self,x):
y=(-self.b-self.w[:,0]*x)/self.w[:,1]
return y
def Show(self):
plt.show()
if __name__ == '__main__':
samples,labels=creatdata1()
weights,bias=MyPerceptron(samples,labels)
print '最终训练得到的w和b为:',weights,',',bias
Picture=Picture(samples,weights,bias)
Picture.Show()
实验结果:
最终训练得到的w和b为: [[-2. 4.]] , [ 0.]
算法三
利用sklearn包中的感知器算法,并进行测试与评估
# -*- encoding:utf-8 -*-
'''
利用sklearn中的的Perceptron进行实验,并进行测试
'''
from sklearn.datasets import make_classification
from sklearn.linear_model import Perceptron
from sklearn.cross_validation import train_test_split
from matplotlib import pyplot as plt
import numpy as np
#利用算法进行创建数据集
def creatdata():
x,y = make_classification(n_samples=1000, n_features=2,n_redundant=0,n_informative=1,n_clusters_per_class=1)
'''
#n_samples:生成样本的数量
#n_features=2:生成样本的特征数,特征数=n_informative() + n_redundant + n_repeated
#n_informative:多信息特征的个数
#n_redundant:冗余信息,informative特征的随机线性组合
#n_clusters_per_class :某一个类别是由几个cluster构成的
make_calssification默认生成二分类的样本,上面的代码中,x代表生成的样本空间(特征空间)
y代表了生成的样本类别,使用1和0分别表示正例和反例
y=[0 0 0 1 0 1 1 1... 1 0 0 1 1 0]
'''
return x,y
if __name__ == '__main__':
x,y=creatdata()
#将生成的样本分为训练数据和测试数据,并将其中的正例和反例分开
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=0)
#正例和反例
positive_x1=[x[i,0]for i in range(len(y)) if y[i]==1]
positive_x2=[x[i,1]for i in range(len(y)) if y[i]==1]
negetive_x1=[x[i,0]for i in range(len(y)) if y[i]==0]
negetive_x2=[x[i,1]for i in range(len(y)) if y[i]==0]
#定义感知机
clf=Perceptron(fit_intercept=True,n_iter=50,shuffle=False)
# 使用训练数据进行训练
clf.fit(x_train,y_train)
#得到训练结果,权重矩阵
weights=clf.coef_
#得到截距
bias=clf.intercept_
#到此时,我们已经得到了训练出的感知机模型参数,下面用测试数据对其进行验证
acc=clf.score(x_test,y_test)#Returns the mean accuracy on the given test data and labels.
print '平均精确度为:%.2f'%(acc*100.0)
#最后,我们将结果用图像显示出来,直观的看一下感知机的结果
#画出正例和反例的散点图
plt.scatter(positive_x1,positive_x2,c='red')
plt.scatter(negetive_x1,negetive_x2,c='blue')
#画出超平面(在本例中即是一条直线)
line_x=np.arange(-4,4)
line_y=line_x*(-weights[0][0]/weights[0][1])-bias
plt.plot(line_x,line_y)
plt.show()
实验结果为:平均精确度为:96.00
通过算法三和算法四可以看出,直接调用开源包里面的算法还是比较简单的,思路是通用的。
算法四
我们利用sklearn包中的感知机算法进行分类算法的实现。
# -*- encoding:utf-8 -*-
import numpy as np
'''
以scikit-learn 中的perceptron为例介绍分类算法
应用及其学习分类算法的五个步骤
(1)选择特征
(2)选择一个性能指标
(3)选择一个分类器和一个优化算法
(4)评价模型的性能
(5)优化算法
以scikit-learn 中的perceptron为例介绍分类算法
1 读取数据-iris
2 分配训练集和测试集
3 标准化特征值
4 训练感知器模型
5 用训练好的模型进行预测
6 计算性能指标
7 描绘分类界面
'''
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
iris=datasets.load_iris()
X=iris.data[:,[2,3]]
y=iris.target
#训练数据和测试数据分为7:3
from sklearn.cross_validation import train_test_split
x_train,x_test,y_train,y_test=train_test_split(X,y,test_size=0.3,random_state=0)
#标准化数据
from sklearn.preprocessing import StandardScaler
sc=StandardScaler()
sc.fit(x_train)
x_train_std=sc.transform(x_train)
x_test_std=sc.transform(x_test)
#引入skleran 的Perceptron并进行训练
from sklearn.linear_model import Perceptron
ppn=Perceptron(n_iter=40,eta0=0.01,random_state=0)
ppn.fit(x_train_std,y_train)
y_pred=ppn.predict(x_test_std)
print '错误分类数:%d'%(y_test!=y_pred).sum()
from sklearn.metrics import accuracy_score
print '准确率为:%.2f'%accuracy_score(y_test,y_pred)
#绘制决策边界
from matplotlib.colors import ListedColormap
import warnings
def versiontuple(v):
return tuple(map(int,(v.split('.'))))
def plot_decision_regions(X,y,classifier,test_idx=None,resolution=0.02):
#设置标记点和颜色
markers=('s','x','o','^','v')
colors=('red','blue','lightgreen','gray','cyan')
cmap=ListedColormap(colors[:len(np.unique(y))])
# 绘制决策面
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
alpha=0.8, c=cmap(idx),
marker=markers[idx], label=cl)
if test_idx:
# 绘制所有数据点
if not versiontuple(np.__version__) >= versiontuple('1.9.0'):
X_test, y_test = X[list(test_idx), :], y[list(test_idx)]
warnings.warn('Please update to NumPy 1.9.0 or newer')
else:
X_test, y_test = X[test_idx, :], y[test_idx]
plt.scatter(X_test[:, 0], X_test[:, 1], c='',
alpha=1.0, linewidth=1, marker='o',
s=55, label='test set')
def plot_result():
X_combined_std = np.vstack((x_train_std, x_test_std))
y_combined = np.hstack((y_train, y_test))
plot_decision_regions(X=X_combined_std, y=y_combined,
classifier=ppn, test_idx=range(105,150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
plot_result()
实验结果为:错误分类数:4;准确率为:0.91
<完>
-
- 代码实现
- 算法一
- 算法二
- 算法三
- 算法四
- 代码实现
人生如棋,落子无悔。
-------By Ada