从线性到非线性模型-Fisher线性判别与线性感知机

从线性到非线性模型

1、线性回归，岭回归，Lasso回归，局部加权线性回归

2、logistic回归，softmax回归，最大熵模型

3、广义线性模型

4、Fisher线性判别和线性感知机

5、三层神经网络

6、支持向量机

四、Fisher线性判别与线性感知机

​ Fisher线性判别和线性感知机都是针对分类任务，尤其是二分类，二者的共同之处在于都是线性分类器，不同之处在于构建分类器的思想，但是二者有异曲同工之妙。同时二者又可以与logistic回归进行对比，当然logistic回归的理论基础是概率。

一、Fisher线性判别

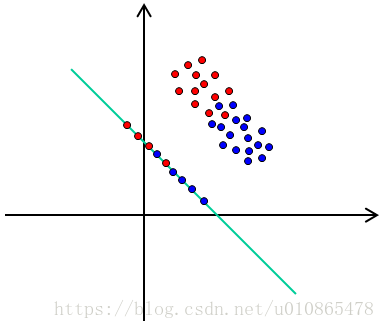
​ Fisher线性判别是一种线性分类思想，其核心是找一个投影方向将d维数据投影（降维）到一维，使得类内紧致，类间分离。在确定投影方向之后，决策分类器还并未完成，我们还需要分界点来划分不同的类。一般而言很少用Fisher线性判别作为分类模型，更多是借鉴Fisher线性判别的思想来指导降维。

以两类问题来分析：

由类内紧致，类间分离准则确定投影方向，我们可以定义如下类内距离和类间距离

m~i=1ni∑yj∈Xii=1,2yj=1ni∑yj∈Xii=1,2wTxj=wTmi m ~ i = 1 n i ∑ y j ∈ X i i = 1 , 2 y j = 1 n i ∑ y j ∈ X i i = 1 , 2 w T x j = w T m i

其中 m~i m ~ i 表示降维后的类中心， mi m i 表示原始空间的类中心。

类内距离：

S~w=∑yj∈Xii=1,2(yj−m~i)2=∑xj∈Xii=1,2⎛⎝wTxj−1ni∑xj∈XiiwTxj⎞⎠2=wT∑xj∈Xii=1,2⎛⎝xj−1ni∑xj∈Xiixj⎞⎠2w=wTSww(1) (1) S ~ w = ∑ y j ∈ X i i = 1 , 2 ( y j − m ~ i ) 2 = ∑ x j ∈ X i i = 1 , 2 ( w T x j − 1 n i ∑ x j ∈ X i i w T x j ) 2 = w T ∑ x j ∈ X i i = 1 , 2 ( x j − 1 n i ∑ x j ∈ X i i x j ) 2 w = w T S w w

其中 Sw=∑i=1,2xj∈Xi(xj−mi)2 S w = ∑ x j ∈ X i i = 1 , 2 ( x j − m i ) 2 表示每类样本在原始空间的一个类内距离。

类间距离：

S~b=(m~1−m~2)2=⎛⎝1n1∑xj∈X1wTxj−1n2∑xj∈X2wTxj⎞⎠2=wT⎛⎝1n1∑xj∈X1xj−1n2∑xj∈X2xj⎞⎠2w=wTSbw(2) (2) S ~ b = ( m ~ 1 − m ~ 2 ) 2 = ( 1 n 1 ∑ x j ∈ X 1 w T x j − 1 n 2 ∑ x j ∈ X 2 w T x j ) 2 = w T ( 1 n 1 ∑ x j ∈ X 1 x j − 1 n 2 ∑ x j ∈ X 2 x j ) 2 w = w T S b w

其中 Sb=∑i=1,2xj∈Xi(m1−m2)2 S b = ∑ x j ∈ X i i = 1 , 2 ( m 1 − m 2 ) 2 表示每类样本在原始空间的一个类间距离。

所以为了使类内紧致，类间分离，可以最大化如下目标函数：

maxJ(w)=S~bS~w=wTSbwwTSww max J ( w ) = S ~ b S ~ w = w T S b w w T S w w

等价于 max(wTSbw)s.t.wTSww=c max ( w T S b w ) s . t . w T S w w = c ,由拉格朗日乘子法有

L(w,λ)=wTSbw−λ(wTSww−c) L ( w , λ ) = w T S b w − λ ( w T S w w − c )

可以看出目标函数是关于w的二次凸规划，极值在导数为0处取到，对上式求导有 Sbw∗−λSww∗=0 S b w ∗ − λ S w w ∗ = 0 ,如果 Sw S w 可逆的话，即

(Sb−λSw)w=0S−1wSbw∗=λw∗ ( S b − λ S w ) w = 0 S w − 1 S b w ∗ = λ w ∗

也就是说 w w 是 (Sb−λSw) ( S b − λ S w ) 的特征向量。将 Sb=(m1−m2)2 S b = ( m 1 − m 2 ) 2 带入有

S−1w(m1−m2)(m1−mT2)w∗=λw∗ S w − 1 ( m 1 − m 2 ) ( m 1 − m 2 T ) w ∗ = λ w ∗

又 (m1−mT2)w∗ ( m 1 − m 2 T ) w ∗ 是一个标量，所以 w∗=S−1w(m1−m2) w ∗ = S w − 1 ( m 1 − m 2 ) .

​ 虽然我们确定了投影方向，但是真正的决策函数还是未能确定，一般最简单的做法是直接在一维上找一个阈值直接将两类分开，但是如何确定阈值还需要定义分类的损失函数（类一致性准则）。

比如我们直接采用0-1损失，那么决策界则尽可能多的正确分类样本，另外如果我们采用Logistic回归的对数损失，那么我们的决策边界就不一样。从这个角度来看，线性判别分析和Logistic回归都是将数据映射到一维来进行分类，有没有不用降维直接进行分类的方法，下面就是感知机的分类思想。

二、线性感知机

​ 线性感知机同样是基于线性分类思想，其核心是直接在高维空间找到一个超平面将两类样本尽可能的分开。即，定义点到超平面的距离，在保证线性可分的基础上最小化点到超平面的距离（等价于使得最难分的样本离超平面距离尽可能的大），但由于没有线性可分前提，所以感知机的目标函数是最小化错分样本到超平面的距离之和（线性损失），而分类正确的样本无损失。

首先定义线性超平面：

w⋅x+b=0 w ⋅ x + b = 0

点到超平面的距离为 1||w||2(w⋅xi+b) 1 | | w | | 2 ( w ⋅ x i + b ) ，即错分的样本到超平面的距离一定为负：

−1||w||2yi(w⋅xi+b)>0 − 1 | | w | | 2 y i ( w ⋅ x i + b ) > 0

感知机只考虑分类错误的样本，目标函数为最小化错分样本到超平面的距离之和：

min−∑xi∈M1||w||2yi(w⋅xi+b) min − ∑ x i ∈ M 1 | | w | | 2 y i ( w ⋅ x i + b )

其中M为错分样本集合。因为感知机优化的目标是针对错误样本集来不断的调整参数，所以在使用梯度下降算法的时候梯度的计算只依赖于错分的样本。

找到超平面之后我们就可以基于超平面定义决策函数为

f(x)=sign(w⋅x+b)sign(x)={+1，x≥0−1,x<0 f ( x ) = s i g n ( w ⋅ x + b ) s i g n ( x ) = { + 1 ， x ≥ 0 − 1 , x < 0

再回过头看损失函数，我们发现感知机的损失与Logistic回归的对数损失不一样，感知机采用的损失直接是错误样本的 f(x) f ( x ) 值，而Logistic回归的损失是所有样本的对数损失（当然Logistic回归的 f(x)=sigmoid(x) f ( x ) = s i g m o i d ( x ) ）。

感知机的对偶形式

感知机的对偶形式是logistic回归一致，同SVM对偶形式推导一致

​ 可以说神经网络和SVM都是线性感知机的一种延伸，神经网络是引入非线性激活函数，而SVM则是使用核函数，SVM同时提出了软间隔分类。虽然说神经网络是从感知机过来的，但是神经网络引入非线性激活函数后，不仅失去了解释性，也使其与感知机渐行渐远，笔者倒是觉得SVM更像感知机，不仅提升了精度，同时保留了很好的解释性。