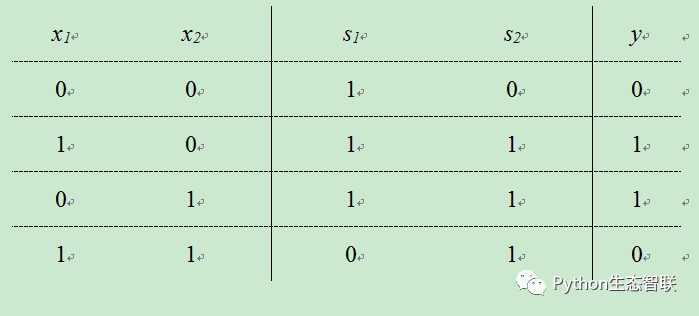多层感知机不等于神经网络？

    在前一章节（https://blog.csdn.net/u012132349/article/details/86166324），我们介绍了感知机可以实现与门、或门、非门。只需给定合适的参数(w1, w2, b)并利用Python就可以简单实现对输入的任意(x1,x2)，输出0或1。

    今天我们将介绍感知机的局限性(严格说是单层感知机的局限性)。这里我们想用感知机实现异或门，所谓异或门，指的是只有x1或x2中的一方为1时，才会输出1，真值表如下图所示：

                                                   

    读者可尝试用前面介绍的感知机去实现这个异或门，您可以设置任意的(w1, w2, b)值，看看对输入的任意(x1,x2)，输出是否一定满足上图的条件。实际上，用前面介绍的单层感知机是无法实现这个异或门的。下面我们通过画图的方式来分析这个问题。首先，我们试着将前面介绍的与非门的动作形象化，当权重(w1,w2,b)=(-0.5,-0.5,0.7)时感知机可用下式表示：

                                                 

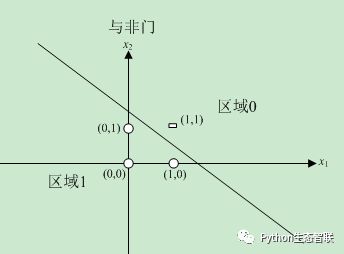
    与非门表明只要有一个输入信号为0，则输出就为1，上式满足此条件。该公式表示的感知机生成了由直线0.7-0.5x1-0.5x2=0分割开的两个空间，如下图所示，一个空间输出0，一个空间输出1。

                                              

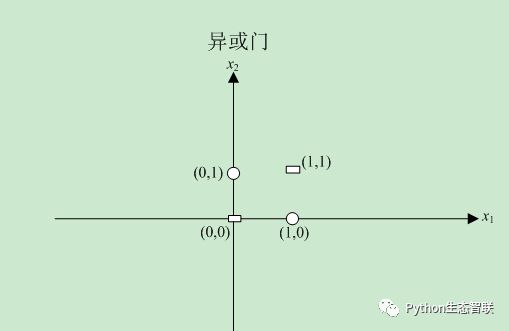
    不难验证，与非门在(x1,x2)等于(0,0)、(1,0)、(0,1)时输出为1，在(x1,x2)等于(1,1)时输出为0。实际上图中的那条线就将这四个点正确地分开了。同样地，我们将异或门的真值表在图中标记出来。如下图所示。

                                      

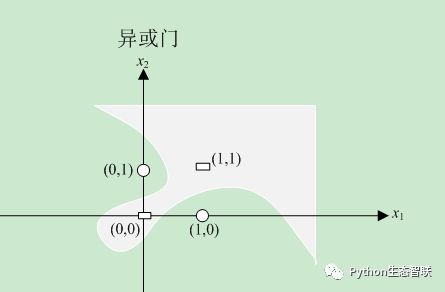
    图中，(x1,x2)等于(0,0)、(1,1)时输出为0，在(x1,x2)等于(0,1)和(1,0)时输出为1。显然已经不能用一条直线将图中的０和□分割开来。事实上一条直线是无法将它们分割开来的，只能用下图所示的曲线将它们分割开来。

                                         

    可见，单层感知机的局限性就在于它只能表示由一条直线分割的空间（称为线性空间）。像上图这样的弯曲的曲线是无法用单层感知机表示。说明一下，曲线分割的空间称为非线性空间。

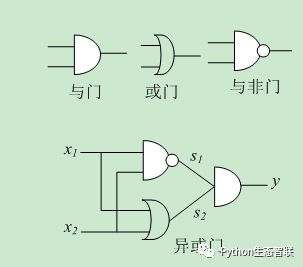
    由上面的分析可知单层感知机无法表示异或门，即单层感知机无法分离非线性空间。因此需要组合感知机（叠加层）来实现异或门，这里先不考虑叠加层具体是指什么。在电路专业中，可以通过组合与门、非门、或门实现异或门。如下图所示。

                                                     

    从图中可知，x1和x2是与非门和或门的输入，而与非门和或门的输出则是与门的输入。图中的s1是与非门的输出，s2是或门的输出。s1和s2作为与门的输入，y作为与门的输出。现在给出异或门的真值表如下所示：

                              

   观察真值表x1、x2、y，可以发现确实符合异或门的输出。使用Python可轻松实现异或门，如下所示：

import numpy as np

def yufei(x1,x2):
    """与非门的实现"""
    x=np.array([x1,x2])
    w=np.array([-0.5,-0.5])
    b=0.7
    value=np.sum(w*x)+b
    if value<=0:
        return 0
    else:
        return 1

def huo(x1,x2):
    """或门的实现，只有参数不一样"""
    x=np.array([x1,x2])
    w=np.array([0.5,0.5])
    b=-0.2
    value=np.sum(w*x)+b
    if value<=0:
        return 0
    else:
        return 1

def yu(x1,x2):
    """与门的实现，只有参数不一样"""
    x=np.array([x1,x2])
    w=np.array([0.5,0.5])
    b=-0.7
    value=np.sum(w*x)+b
    if value<=0:
        return 0
    else:
        return 1  

def yihuo(x1,x2):
    """异或门的实现"""
    s1=yufei(x1,x2)
    s2=huo(x1,x2)
    y=yu(s1,s2)
    return y

yihuo(0,0)  #输出0
yihuo(1,0)  #输出1
yihuo(0,1)  #输出1
yihuo(1,1)  #输出0

    下面用感知机的表示方法来表示这个异或门，如下图所示。异或门是一种多层结构的神经网络(简单来说，就是多层感知机)。这里将最左边的一列称为第0层，中间的一列称为第1层，最右边的一列称为第二层。前面介绍的与门、或门等都是单层感知机，异或门是2层感知机(第0层没有权重，所以这里不算)。叠加了多层的感知机也称为多层感知机。可见通过叠加层(加深层)能够进行非线性的表示。

                                              

    上图中的2层感知机，先在第0层和第1层的神经元之间进行信号的传递和接收，然后在第1层和第2层之间进行信号的传送和接收。通过异或门的实现，我们不难理解，可以通过增加层来实现更复杂的电路，像加法运算的加法器也可以用感知机实现。实际上，只需要通过与非门的组合，就能再现计算机进行的处理，这说明使用感知机也可以表示计算机(当然这不是我们所关心的)。

    本章主要讲解了单层感知机的局限性，并引出2层感知机来表示异或门。这里提到了多层感知机组成了神经网络，当然神经网络没这么简单，但是它和多层感知机是有很多共同点，如果你掌握了文章中介绍的2层感知机，相信对你学习神经网络是非常有帮助的。后面我们将正式进入神经网络的学习！ 欢迎关注我的博客，有欢迎欢迎关注我的微信公众号“Python生态智联”