GPU加速的编程思想，图解，和经典案例，NVIDIA Python Numba CUDA大法好

0 前言

2018年7月到9月，我做一个项目，Python编程实现。Python程序写出来了，但是很慢。Python的for loop真是龟速呀。这个程序的瓶颈部分，就是一个双层for loop，内层for loop里是矩阵乘法。于是乎想到了numba来给瓶颈部分做优化。简单的@numba.jit可以加速几十倍，但是很奇怪无法和joblib配合使用。

最终解决方案是使用@numba.cuda.jit，他可以轻松加速数千倍 — 这篇博客就带你入门GPU编程，本文出了阐述我对于GPU编程的理解和小结，还引用了一些非常好的学习资料。我这里说的GPU，专门指的是NVIDIA GPU的CUDA编程。

---

1 GPU 编程思想

传统意义上来讲，大部分程序是运行在CPU上的，GPU只是玩游戏的时候派上用场。然而现在GPU的重要性大幅度提升，NVIDIA的股票也是高速上涨，因为GPU除了游戏，增加了一个killer app：机器学习。另外，比特币挖矿也是要用GPU的。

1. 编写CPU的程序，有两个特点：单线程思想，面向对象思想。
2. 编写GPU的程序，有两个特点：千线程思想，面向数组思想。

1.1 千线程思想

CPU当然也有多线程程序，比如Macbook Pro是双核四线程，可以同时跑四个线程（有点不准确，不过意思）。但是CPU的多线程和GPU的多线程有两点本质区别：1）CPU的“多”，规模是十，然而GPU的“多”，规模是千；2）CPU多线程之间的并行，是多个function之间的并行，然而GPU多线程的并行，是一个function内部的并行。

图1：本图和下文很多图片，来自这个链接

进一步解释第二点，假设一个$function$内部是一个双层for loop i := 0 $\cdots$ 999，程序需要调用四次$function$。那么CPU的程序会同时搞出四个线程，每个线程调用一次function，每次顺序执行for loop$1000^2$次。而GPU的骚操作是，顺序调用四次function，每次搞出$1000^2$个线程一下子解决这个双层for loop。当然了，你需要改写程序，改为$function\_gpu$（GPU里面可以同时执行几千的线程，其他线程处于等待状态，不过你尽管搞出上百万个线程都没问题）。当然了，你可以CPU和GPU同时配合使用，CPU搞出四个线程，每个线程调用$function\_gpu$，这样子可以增大GPU的利用率。

这里申明很重要一点，不是所有的$function$能(适合)改写为$function\_gpu$。不过很多机器学习相关的算法，很多计算密集行算法，是可以改写的。会把$function$改写为$function\_gpu$是一种当下少数人掌握的技能。在本文chapter 3将讲解几乎是的GPU编程的Hello world。

1.2 面向数组思想

面向对象的编程思想是当下主流思想：一个对象有若干个属性，一个容器装很多个对象，如果想获取对象的属性，需要获取对象然后进行点操作。面向数组则完全不同。在做data science(DS) 和 machine learning(ML) 项目的时候，都是面向数组的思想。numpy.ndarray，pandas.DataFrame，和torch.Tensor都是设计的非常棒的”超级数组"，其中torch.Tensor原生支持GPU。

在DS和ML项目里面，数组之所以作为唯一钦定的数据结构，我认为是数组能够完美胜任DS和ML 项目里面组织和管理数据的工作。DS和ML项目完全不需要object-oriented的那一套封装和继承的思想，也不需要链表、栈、队列、哈希表、二叉树、B-树、图等其他数据结构。这背后的原因，我认为是DS和ML项目和那种企业级开发存在天然的区别。比如企业级开发需要处理复杂的业务逻辑，DS和ML项目就没有复杂的业务逻辑，只有对数组里的数据的反复“暴力计算”，这种对一个数组里的数据进行反复的暴力计算，正好是GPU说擅长的东西，SIMD(single instruction multiple data)既视感。

图2：截屏自这个YouTube视频。

所以我在使用GPU加速的方法来对程序进行改造的时候，我给类写了一个 to_array(self) 的方法，为了把类的非numpy.array数据成员转换成numpy.array数据成员。

---

2 图解GPU

图3：CPU里面有很大的缓存(黄色)，GPU里面缓存很少。CPU擅长复杂的程序控制(蓝色)，但是ALU算术运算单元(绿色)比较少。GPU最大的特点就是ALU很多，擅长算数计算。

图4：GPU加速的方法是，把程序里面计算密集型的CPU代码，改写为GPU代码。让CPU做CPU擅长的事情，让GPU做GPU擅长的事情，优势互补。

图5：GPU是如何和内存和CPU相配合的，分为4个步骤。其中步骤1和4是很消耗时间的，实际编程的时候，需要考虑如何减少1和4。

图6：CUDA是这样子组织上千个线程的，若干线程汇聚为一个block，若干block汇聚为一个grid。这就是CUDA的two-level thread hierarchy。深刻理解这个two-level对于编写CUDA程序十分重要。

图7：GPU的内存模型。GPU里面的内存分为三种：per thread local memory， per block shared memory，和global memory。在实际编程的时候，需要考虑多用shared memory，少用global memory，因为shared比global的访问和存取速度快很多。

---

3 GPU的Hello world: 矩阵相乘

能够让人理解GPU编程的 Hello world 程序，便是矩阵相乘。这个纽约大学的教程非常棒，详细讲解了如何编写GPU程序进行矩阵相乘。我当时学习Numba和CUDA，这个教程发挥了很大的作用。

3.1介绍几个名词

首先，要弄清楚下面6个名词的概念。编写GPU程序，其实是一种CPU和GPU之间的“互动”，所谓的异构开发。

1. Host。代表CPU。
2. Device。代表GPU。
3. Host memory。RAM内存。
4. Device memory。GPU上的存储。
5. Kernal function。GPU函数，执行在device上面，调用者是host。
6. Device function。GPU函数，执行在device上面，调用者是kernal function或者device function。

3.2 GPU程序的执行流程

图5可视化了GPU程序的流程：

1. 把数组的数据(numpy.ndarray)从host memory拷贝到device memory上。
2. 配置kernal function的参数，调用kernal function。参数有两种：一种用中括号[ ]，一种用小括号( )。中括号的参数是threadperblock和blockpergrid，参考图6。小括号就是那种普通函数的参数。
3. 几千个线程同时调用同一个kernal function，在GPU里面进行计算。kernal function的编写，是一门技术。
4. 把GPU里面的运算结果，从device memory拷贝回host memory。THE END。

3.3 矩阵相乘源代码

这份Python代码，有6个函数，进行 $\mathbf{C}=\mathbf{A}\times \mathbf{B}$

1. cpu_mat_mul(A, B, C), 基于CPU的矩阵相乘，$O(n^3)$。
2. cpu_mat_mul_jit(A, B, C)，和cpu_mat_mul相比，唯一的区别就是加了装饰器 @jit，这是一种编译优化工具，可以加快几十倍。
3. mat_mul_naive_kernal(A, B, C)，矩阵相乘的GPU函数，使用global memory。
4. mat_mul_shared_kernal(A, B, C)，矩阵相乘的GPU，使用了shared memory。shared memory比global memory访问速度快不少。
5. host_naive(A, B, C)，mat_mul_naive_kernal的“配套设施”，kernal不能独立存在的，前前后后需要一些代码辅助。
6. host_optimized(A, B, C)，mat_mul_shared_kernal的“配套设施”。如果host_naive比cpu_mat_mul快三千倍的话，host_optimized可能快三千五百倍。

---

我在学习Numba CUDA的时候，使用的Anaconda Python3.6，Numba 0.38， cudatoolkit 9.0。

'''
Matrix multiplication sample, some numba and CUDA testing code
'''
import math
import time
import numpy as np
from numba import cuda, jit, float64

TPB = 16 # thread per block

def cpu_mat_mul(A, B, C):
    '''matrix mulplication on cpu, O(n^3) implementation
    '''
    for i in range(C.shape[0]):
        for j in range(C.shape[1]):
            summation = 0
            for k in range(A.shape[1]):
                summation += A[i, k] * B[k, j]
            C[i, j] = summation

@jit
def cpu_mat_mul_jit(A, B, C):
    '''matrix mulplication on cpu O(n^3) implementation with @jit decocation
    '''
    for i in range(C.shape[0]):
        for j in range(C.shape[1]):
            summation = 0
            for k in range(A.shape[1]):
                summation += A[i, k] * B[k, j]
            C[i, j] = summation

@cuda.jit
def mat_mul_naive_kernal(A, B, C):
    '''matrix multiplication on gpu, naive method using global device memory
    '''
    i, j = cuda.grid(2)
    if i < C.shape[0] and j < C.shape[1]:
        summation = 0
        for k in range(A.shape[1]):
            summation += A[i, k] * B[k, j]
        C[i, j] = summation

@cuda.jit
def mat_mul_shared_kernal(A, B, C):
    '''matrix multiplication on gpu, optimized version using shared memory.
    '''
    s_A = cuda.shared.array((TPB, TPB), dtype=float64)  # s_ --> shared
    s_B = cuda.shared.array((TPB, TPB), dtype=float64)
    x, y = cuda.grid(2)
    tx = cuda.threadIdx.x
    ty = cuda.threadIdx.y
    bw = cuda.blockDim.x
    bh = cuda.blockDim.y
    #print((x, y), (tx, ty), (bx, by), (bw, bh))

    if x >= C.shape[0] or y >= C.shape[1]:
        return

    tmp = 0
    for i in range(int(A.shape[1]/TPB)):
        #print((x, y), (tx, ty), i)
        s_A[tx, ty] = A[x, ty + bw*i]
        s_B[tx, ty] = B[tx + bh*i, y]
        cuda.syncthreads()

        for j in range(TPB):
            tmp += s_A[tx, j] * s_B[j, ty]

        cuda.syncthreads()
    C[x, y] = tmp


def host_naive(A, B, C):
    '''host code for calling naive kernal
    '''
    d_A = cuda.to_device(A)  # d_ --> device
    d_B = cuda.to_device(B)
    d_C = cuda.device_array(C.shape, np.float64)

    threadsperblock = (TPB, TPB)
    blockspergrid_x = math.ceil(A.shape[0]/threadsperblock[0])
    blockspergrid_y = math.ceil(B.shape[1]/threadsperblock[1])
    blockspergrid = (blockspergrid_x, blockspergrid_y)

    mat_mul_naive_kernal[blockspergrid, threadsperblock](d_A, d_B, d_C)

    return d_C.copy_to_host()


def host_optimized(A, B, C):
    '''host code for calling naive kernal
    '''
    d_A = cuda.to_device(A)  # d_ --> device
    d_B = cuda.to_device(B)
    d_C = cuda.device_array(C.shape, np.float64)

    threadsperblock = (TPB, TPB)
    blockspergrid_x = math.ceil(A.shape[0]/threadsperblock[0])
    blockspergrid_y = math.ceil(B.shape[1]/threadsperblock[1])
    blockspergrid = (blockspergrid_x, blockspergrid_y)

    mat_mul_shared_kernal[blockspergrid, threadsperblock](d_A, d_B, d_C)

    return d_C.copy_to_host()


def main():
    '''main
    '''
    A = np.full((TPB*4, TPB*6), 0.5, dtype=np.float64)
    B = np.full((TPB*6, TPB*2), 2, dtype=np.float64)
    C = np.full((TPB*4, TPB*2), 0, dtype=np.float64)

    start = time.time()
    cpu_mat_mul(A, B, C)
    print('cpu mat mul:', time.time()-start)

    start = time.time()
    cpu_mat_mul_jit(A, B, C)
    print('cpu mat mul with numba.jit:', time.time()-start)

    start = time.time()
    ans = host_naive(A, B, C)
    print('gpu mat mul global:', time.time()-start)
    print(ans)
    
    start = time.time()
    ans = host_optimized(A, B, C)
    print('gpu mat mul shared:', time.time()-start)
    print(ans)

if __name__ == '__main__':
    main()

3.4 理解GPU的矩阵相乘算法的关键

$\mathbf{C}=\mathbf{A}\times \mathbf{B}$
假设A.shape = (64, 96), B.shape = (96, 32)，那么C.shape = (64, 32)，即C矩阵有2048个元素。

1. CPU的算法，是1个线程，顺序依次计算2048个元素的值。
2. GPU的算法，是同时开出2048个线程，每个线程计算一个元素的值。线程与线程之间是并行的。

目前最新的英伟达GeForce RTX 2070，可以同时开出2304个线程，2048个线程简直是轻松无压力。

3.5 作图：Y轴时间，X轴数组的长度

作图代码：GitHub链接（有时候GitHub无法加载Jupyter Notebook，此时点这个nbviewer）

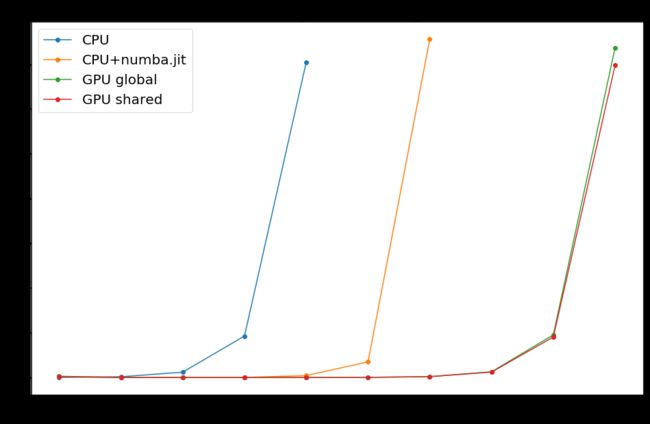
1. $2^9=512$ ，此时 CPU 超过一分钟了
2. $2^{11}=2048$ ，此时 CPU+numba.jit 超过一分钟了
3. $2^{14}=16384$ ，此时 GPU 超过一分钟了

一个(16384, 16384)的数组，在Python里面已经超过2G的内存了，这样大的数组在CPU和GPU之间传输是需要花不少时间的。

3.6 优化时间

shared memory 充其量是一个小优化，真正的大优化是减少CPU和GPU之间的通信时间（本质上是内存和GPU显存之间的通信）。

我的亲身例子：

1. GPU里，一个大数组的每个元素计算好了，把大数组从GPU传输到内存，使用CPU求和 numpy.sum()
2. GPU里， 一个大数组的每个元素计算好了，大数组原地不动，使用GPU求和(cuda.reduce)，给CPU传输求和结果（一个float）。

方法2 和方法1相比，GPU向CPU的传输降低了很多，CPU做求和和GPU做求和速度差不多。最终时间从1降低到0.5，时间降低50%，或者加速1倍。我发现，CPU和GPU之间的通信是非常耗费时间的。要降低CPU和GPU之间的通信，有时候是需要改变一下算法的。

---

$$TheEnd$$

$$喜欢记得点赞哟$$

---

Last update: 3/22/2019