超级简单的神经网络——训练数据分类(python语言)

需要kddtrain2018.txt和kddtest2018.txt的盆友，请下载我上传的资源：神经网络训练数据分类_kdd

内容：

根据给定数据集创建分类器。
训练数据集(kddtrain2018.txt)：100 predictive attributes A1,A2,...,A100和一个类标C，每一个属性是介于0～1之间的浮点数，类标C有三个可能的{0，1，2}，给定的数据文件有101列，6270行。
测试数据集(kddtest2018.txt)：500行

处理过程：

1.将两个txt文件转换成excel，得到6270*101、500*100(test2018.xlsx)的两个.xlsx表格。

2.将训练文件6270*101分成两个表格：6000*101和270*101，得到train2018.xlsx文件和val2018.xlsx文件。

3.用train2018.xlsx代码训练

4.用val2018.xlsx验证，得到准确率96.7%

5.可以预测test结果，但是没有标签，所以不知道正确率......此步略：）

神经网络设计：

原则：简单点，写代码的方式简单点

三层网络，输入层，隐含层，输出层。

n_x=6000（6000个训练样本），n_h=32（32个神经元，也可以是别的数字），n_y=3（3类）

训练代码：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

def initialize_parameters(n_x, n_h, n_y):
    W1 = np.random.randn(n_h,n_x) * 0.01
    b1 = np.zeros((n_h,1))
    W2 = np.random.randn(n_y,n_h) * 0.01
    b2 = np.zeros((n_y,1))
  
    assert (W1.shape == (n_h, n_x))
    assert (b1.shape == (n_h, 1))
    assert (W2.shape == (n_y, n_h))
    assert (b2.shape == (n_y, 1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

def forward_propagation(X, parameters):
   
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]

    # Implement Forward Propagation to calculate A2 (probabilities)
    Z1 = np.dot(W1,X)+b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2,A1)+b2
    A2 = sigmoid(Z2)
    #print(W2.shape)
    #print(A2.shape)
    
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    
    return A2, cache

def compute_cost(A2, Y, parameters):
    #计算损失时，用的是转换之后的标签
    #m = Y.shape[1] # number of example

    # Compute the cross-entropy cost
    logprobs = -np.multiply(np.log(A2),Y)
    cost = np.sum(logprobs)/A2.shape[1]
    #print(logprobs.shape)
    #print(cost.shape)
    return cost

def backward_propagation(parameters, cache, X, Y):
    #反向传播时，用的也是转换之后的标签Y->label_train
    m = X.shape[1]
    
    W1 = parameters["W1"]
    W2 = parameters["W2"]
        
    A1 = cache["A1"]
    A2 = cache["A2"]
    
    # Backward propagation: calculate dW1, db1, dW2, db2. 
    dZ2 = A2-Y
    dW2 = np.dot(dZ2,A1.T)/m
    db2 = np.sum(dZ2,axis=1,keepdims=True)/m
    dZ1 = np.dot(W2.T,dZ2)*(1 - np.power(A1, 2))
    dW1 =  np.dot(dZ1,X.T)/m
    db1 = np.sum(dZ1,axis=1,keepdims=True)/m
    
    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}
    
    return grads

# GRADED FUNCTION: update_parameters

def update_parameters(parameters, grads, learning_rate = 1.2):
   
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]

    # Update rule for each parameter
    W1 = W1-learning_rate*dW1
    b1 = b1-learning_rate*db1
    W2 = W2-learning_rate*dW2
    b2 = b2-learning_rate*db2
   
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

#softmax函数定义
def softmax(x):
    exp_scores = np.exp(x)
    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
    return probs
def sigmoid(x):
    s=1/(1+np.exp(-x))
    return s

data = pd.read_excel('train2018.xlsx',header = None)
train = np.array(data)

X = train[:,0:100]
Y = train[:,100]
Y = Y.reshape((Y.shape[0],1))
#print(X.shape)
#print(X)
#print(Y.shape) # 1*6100
#print(Y)

X = X.T
Y = Y.T
n_x = X.shape[0]
n_h = 32
n_y = 3

parameters = initialize_parameters(n_x, n_h, n_y)


num_iterations = 30000
nuber = Y.shape[1]
label_train=np.zeros((3,nuber))
#根据Y值，转换分类标签，这里有三类输出:{0，1，2}
#Y为1*6100，转换之后为3*6000
for k in range(nuber):
    if Y[0][k] == 0:
        label_train[0][k] = 1
    if Y[0][k] == 1:
        label_train[1][k] = 1
    if Y[0][k] == 2:
        label_train[2][k] = 1
    #label_train[int(Y[0][i])][i]=1
    
#print(label_train.shape)
#print(label_train)
for i in range(0, num_iterations):
    learning_rate=0.05
    #if i>1000:
       # learning_rate=learning_rate*0.999
    # Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache".
    A2, cache = forward_propagation(X, parameters)
        
    pre_model = softmax(A2)
    #pre_model = A2
        
    # Cost function. Inputs: "A2, Y, parameters". Outputs: "cost".
    cost = compute_cost(pre_model, label_train, parameters)
 
    # Backpropagation. Inputs: "parameters, cache, X, Y". Outputs: "grads".
    grads = backward_propagation(parameters, cache, X, label_train)
 
    # Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters".
    parameters = update_parameters(parameters, grads, learning_rate)  
        
        # Print the cost every 1000 iterations
    if i % 1000 == 0:
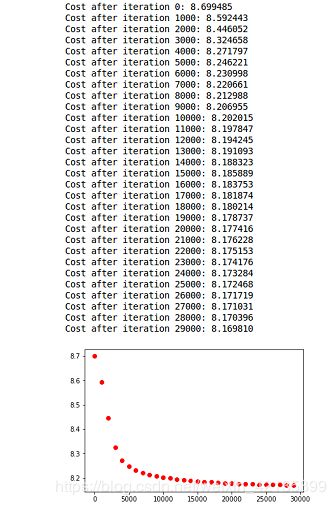
        print ("Cost after iteration %i: %f" %(i, cost))
        plt.plot(i, cost, 'ro')

训练结果： 

验证代码：

data = pd.read_excel('val2018.xlsx',header = None)
test = np.array(data)

X_test = test[:,0:100]
Y_label = test[:,100]
Y_label = Y_label.reshape((Y_label.shape[0],1))

X_test = X_test.T
Y_label = Y_label.T
count = 0
a2,xxx=forward_propagation(X_test,parameters)

for j in range(Y_label.shape[1]):
    #np.argmax返回最大值的索引
    predict_value=np.argmax(a2[:,j])
    #在val上计算准确度
    if predict_value==int(Y_label[:,j]):
        count=count+1
print(np.divide(count,Y_label.shape[1]))

验证结果：

输出：0.9666666666666667

总结：

1.多分类与二分类的损失函数（交叉熵）不一样了！

2.交叉熵刻画的是两个概率分布之间的距离，但神经网络的输出不一定是概率分布，很多情况下是实数。Softmax可以将神经网络前向传播得到的结果变成概率分布。

3.要做分类，得有标签。K分类，标签为K*1维向量

参考：

详解numpy的argmax：https://blog.csdn.net/oHongHong/article/details/72772459

神经网络多分类任务的损失函数——交叉熵：https://blog.csdn.net/lvchunyang66/article/details/80076959

用python的numpy实现神经网络 实现手写数字识别：https://blog.csdn.net/weixin_39504048/article/details/79115437