【统计学习方法by李航】第二章 感知机 个人总结

 
链接：[ 全文章目录 ]

一、感知机模型[2.1]

---

超平面：
输入空间是n维向量，那么超空间就是(n-1)维向量
【键盘字母上面的数字1到0（10个不同的变量），如果想把它们分割开，需要有(10-1)个隔板（9个超空间）】
 
分离超平面（将n整合为2的超平面）：
在一个平面中划一条线，使平面中的样本尽可能的分为正负两类。（一般判断是或不是）

（一）定义2.1

简单定义：【感知机就是 求出分离超平面，再 通过分离超平面来进行二分类 的一种模型。】
 
具体定义：


w∊Rⁿ：叫作权值或权值向量
b∊R  ：叫作偏置
w·x表示w和x的内积（就是点积）

！注意，w和x都是长度为n的向量

感知机是一种 线性分类模型 ，属于 判别模型 。
感知机模型的假设空间是定义在特征空间中的 所有线性分类模型 或 线性分类器 ，
即函数集合 { f | f(x)＝w·x+b } 。

(二)几何解释

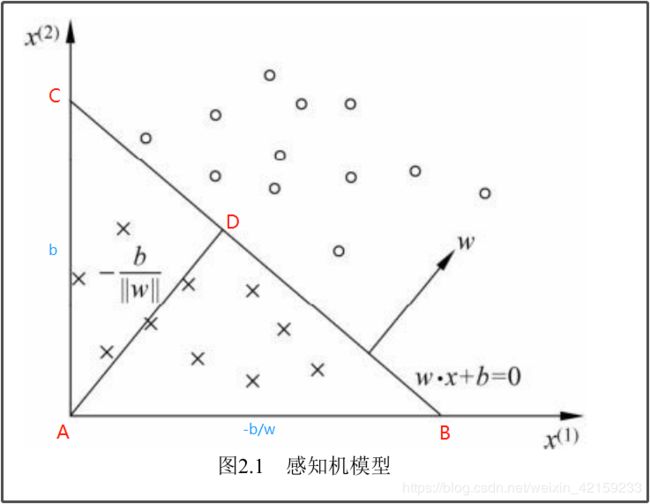
||w||：向量w的2范数是w中各个元素平方之和再开根号，就是向量的模（长度） ；
AD算出来是：$-\frac{b}{\sqrt{1+w^2}}$
怎么变成：$-\frac{b}{||w||}$ 也就是 $-\frac{b}{\sqrt{w^2}}$ 的不是很清楚

 
 

二、感知机学习策略[2.2]

---

（一）数据集的线性可分型[2.2.1]

能用一条线 完全的 分割为两种类型，就称数据集有线性可分型。（不能有一类的某个点跑到另一类里面）

（二）感知机学习策略[2.2.2]

定义（经验）损失函数并将损失函数 极小化 ，求出w、b。
这里的损失函数为：误分类点到超平面（那条线）S的总距离。

具体推倒：

1、把点到直线距离公式摆上来，代入超平面方程

距离$$d=\frac{|A{x}_i+B{y}_i+C|}{\sqrt{A^2+B^2}}$$
已知超平面方程为：w·x+b=0，代入上式，得：
距离$$d=\frac{|w{x}_i+b|}{\sqrt{w^2}}=\frac{|w{x}_i+b|}{||w||}$$
 

2、为了去掉绝对值，我们现在看看误分类数据有什么特点

已知有个误分类的数据(x_i, y_i)
因为它误分类了，所以当：
（1）w·x_i+b>0，即被分类为正类时，它的原分类y_i必为-1(负类)
（2）w·x_i+b<0，即被分类为负类时，它的原分类y_i必为+1(正类)

那么对误分类的数据必有：$$y_i(w\cdot x_i+b)<0$$
而距离是正数，所以在前面加上负号，变成：$$d=-\frac{y_i(w{x}_i+b)}{||w||}$$

【乘上一个 “-y_i” 就可以把绝对值去掉，还可以筛出误分类的数据（正确分类的距离必为负值）】
 

3、推广到多个点

M为误分类点的集合
（1）总距离为：$$-\frac{1}{||w||}\sum _{x_iϵM}{y}_i(w\cdot x+b)$$

（2）因为w是超平面的法向量，与大小无关，而$\frac{1}{||w||}$是一个标量，所以可以忽略$\frac{1}{||w||}$

（3）得到感知机学习的损失函数（经验风险函数）：$$L(w,b)=-\sum _{x_iϵM}{y}_i(w\cdot x+b)$$

（三）损失函数特性

1、非负（距离）
2、正确分类时值为0
3、损失函数是连续可导函数：在误分类时，它是线性函数；正确分类时它是常数函数。
 
 

三、感知机学习算法[2.3]

---

（一）感知机学习算法的原始形式[2.3.1]

通过 梯度下降法 求损失函数的极小值：$$mi{n}_{w,b}L(w,b)=-\sum _{x_iϵM}{y}_i(w\cdot x+b)(2.5)$$

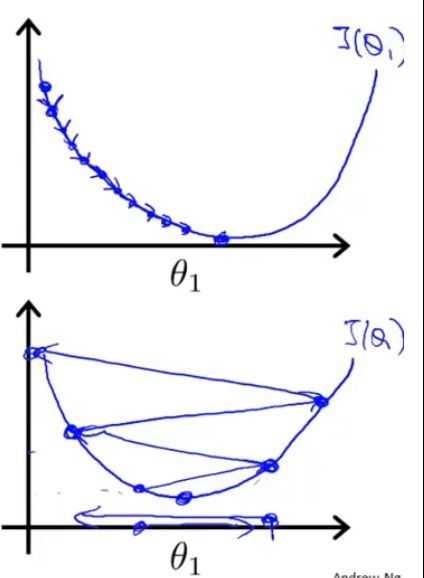
1、梯度下降法的几何解释：通过 不断的运算，使点向 极小值 逼近。

 

2、梯度下降法的具体算法【本章重点】

损失函数的梯度：$$（由2.5对w求偏导）{▽}_{w}L(w,b)=-\sum _{x_iϵM}{y}_i{x}_i$$$$（由2.5对b求偏导）{▽}_{b}L(w,b)=-\sum _{x_iϵM}{y}_i$$
 
（1）任取一个超平面（任取w,b）

（2）得到误分类点的集合M

（3）遍历误分类点求梯度对w,b进行更新：$$w\leftarrow w+\eta y_i{x}_i$$ $$b\leftarrow b+\eta y_i$$

（4）直到L(w,b)=0

$\eta$(0<$\eta$<=1)是步长，又称学习率，用来控制梯度大小。
（在吴恩达的machine learning中，学习率用的是 $\theta$ ）
 

3、梯度下降法的其他解释

当一个实例点被误分类，即位于分离超平面的错误一侧时，则调整w,b的值，使分离超平面向该误分类点的一侧移动，以减少该误分类点与超平面间的距离，直至超平面越过该误分类点使其被正确分类。

4、例2.1（略），通过梯度下降法的具体算法很容易理解

 
 

---

（二）算法的收敛性[2.3.2]（算法收敛的证明）（尽量简化通俗了）

这里证明经过 有限次迭代 可以得到一个将训练数据集 完全正确划分 的分离超平面及感知机模型。

为了便于叙述与推导，
将偏置b并入权重向量w，记作： $\hat{w}$=(w^T,b)^T，
同样也将输入向量加以扩充，加进常数1，记作： $\hat{x}$=(x^T,1)^T 。
这样，$\hat{w}$∊R N+1 ，$\hat{x}$∊R N+1 。 显然，$\hat{w}$·$\hat{x}$＝w·x+b。

结论：

1、对于（1）书中的证明

（1）由于训练数据集是线性可分的，存在超平面可将训练数据集完全正确分开，
取此超平面为${\hat{w}}_{opt}\cdot \hat{x}=w_{opt}\cdot x+b_{opt}=0$，使$||{\hat{w}}_{opt}||=1$。由于对有限的i＝1,2,…,N，均有：$$y_i({\hat{w}}_{opt}\cdot \widehat{x_i})=y_i(w_{opt}\cdot x+b_{opt})>0$$
所以存在$$\gamma =mi{n}_i\{y_i(w_{opt}\cdot x+b_{opt})\}$$
使

$$\ast \ast \ast \ast \ast \ast y_i({\hat{w}}_{opt}\cdot \widehat{x_i})=y_i(w_{opt}\cdot x+b_{opt})\ge \gamma （公式1）\ast \ast \ast \ast \ast \ast$$

（2）解释

1. ${\hat{w}}_{opt}$、w_opt、b_opt的下标opt的意思是：【对任意可选的】$\hat{w}$、w、b。只要满足式子即可。
2. $||{\hat{w}}_{opt}||=1$，原因：${\hat{w}}_{opt}$可以乘上任意常数使公式1都成立，所以，为了特殊化，使${\hat{w}}_{opt}$为单位长度，一般是$||{\hat{w}}_{opt}||=1$
3. $\gamma 就是一个大于0的数，没啥意义$
    

2、对于（2）书中的证明（含解释）

感知机算法从${\hat{w}}_0=0$ （方便后面推导） 开始，如果实例被误分类，则更新权重。

分步证明每一步最终都会得到一个公式，最后进行合并得到推论

分步证明1

---

（1） 令 k-1 是第k个误分类实例之前的扩充权重向量（就是$\hat{w}$在右下角加了个k-1的下标），即
$${\hat{w}}_{k-1}=(w_{k-1}^T,b_{k-1}{)}^T$$

---

（2） 则第k个误分类实例的前提条件（第k次更新前的损失函数）是【这里是把上面的$w_{k-1}$和$b_{k-1}$代入了损失函数】
$$y_i({\hat{w}}_{k-1}\cdot {\hat{x}}_i)=y_i(w_{k-1}\cdot x_i+b_{k-1})\le 0$$
小于0上面有推导，等于0是因为存在没有误分类的情况

---

（3） 若(x_i,y_i)是被${\hat{w}}_{k-1}=(w_{k-1}^T,b_{k-1}{)}^T$误分类的数据，则w和b的更新是
$$w_k\leftarrow w_{k-1}+\eta y_i{x}_i$$ $$b_k\leftarrow b_{k-1}+\eta y_i$$
【就是w和b的更新公式加了个下标】

根据上面的两个更新公式化简得：

$$\ast \ast \ast \ast \ast \ast {\hat{w}}_k={\hat{w}}_{k-1}+\eta y_i{\hat{x}}_i（公式2）\ast \ast \ast \ast \ast \ast$$

化简过程如下
$$\begin{gathered} {\hat{w}}_k=(w_k^T,b_k{)}^T=w_k+b_k \\ =w_{k-1}+\eta y_i{x}_i+b_{k-1}+\eta y_i \\ =[w_{k-1}+b_{k-1}]+[\eta y_i(x_i+1)] \\ ={\hat{w}}_{k-1}+\eta y_i{\hat{x}}_i \end{gathered}$$

 

分步证明2

---

（4） 由公式2$${\hat{w}}_k={\hat{w}}_{k-1}+\eta y_i{\hat{x}}_i$$
可以求出：$${\hat{w}}_k\cdot {\hat{w}}_{opt}={\hat{w}}_{k-1}\cdot {\hat{w}}_{opt}+\eta [y_i{\hat{x}}_i\cdot {\hat{w}}_{opt}]$$

---

（5）
由公式1（的一部分）$$y_i({\hat{w}}_{opt}\cdot \widehat{x_i})\ge \gamma$$
我们就可以把上面（4）式子里面方括号的东西换掉：
$${\hat{w}}_{k-1}\cdot {\hat{w}}_{opt}+\eta [y_i{\hat{x}}_i\cdot {\hat{w}}_{opt}]\ge {\hat{w}}_{k-1}\cdot {\hat{w}}_{opt}+\eta \gamma$$

---

（6） 我们把（5）中不等式的右边推广一下，得到（$\eta$和$\gamma$都是正的）：
$$左边\ge {\hat{w}}_{k-1}\cdot {\hat{w}}_{opt}+\eta \gamma \ge {\hat{w}}_{k-2}\cdot {\hat{w}}_{opt}+2\cdot \eta \gamma \ge \cdot \cdot \cdot \ge {\hat{w}}_0\cdot {\hat{w}}_{opt}+k\cdot \eta \gamma$$
这里$k>=1,kϵN^{+}$（k是大于等于1的正整数）

由（4）和（5）整理得：$${\hat{w}}_k\cdot {\hat{w}}_{opt}\ge {\hat{w}}_0\cdot {\hat{w}}_{opt}+k\cdot \eta \gamma =k\cdot \eta \gamma （{\hat{w}}_0=0）$$
得到

$$\ast \ast \ast \ast \ast \ast {\hat{w}}_k\cdot {\hat{w}}_{opt}\ge k\cdot \eta \gamma （公式3）\ast \ast \ast \ast \ast \ast$$

 

分步证明3

---

（7） 由分步证明1得出的公式2 “ ${\hat{w}}_k={\hat{w}}_{k-1}+\eta y_i{\hat{x}}_i$ ”，等式两边平方得：
$$||{\hat{w}}_k|{|}^2=||{\hat{w}}_{k-1}|{|}^2+2\cdot {\hat{w}}_{k-1}\cdot \eta y_i{\hat{x}}_i+{\eta }^2{y}_i^2||{\hat{x}}_i|{|}^2$$
因为y_i取正负1，所以$y_i^2=1$，就变成了书中的式子（最后那项少了$y_i^2$）：
$$||{\hat{w}}_k|{|}^2=||{\hat{w}}_{k-1}|{|}^2+2\cdot {\hat{w}}_{k-1}\cdot \eta y_i{\hat{x}}_i+{\eta }^2||{\hat{x}}_i|{|}^2$$

---

（8） 由分步证明1的（2）中式子 “ $y_i({\hat{w}}_{opt}\cdot \widehat{x_i})\le 0$ ”；再由于“步进$\eta$”必大于0
所以（7）最后式子中的$$2\cdot {\hat{w}}_{k-1}\cdot \eta y_i{\hat{x}}_i（必定小于等于0）$$
即有：$$||{\hat{w}}_{k-1}|{|}^2+2\cdot {\hat{w}}_{k-1}\cdot \eta y_i{\hat{x}}_i+{\eta }^2||{\hat{x}}_i|{|}^2\le ||{\hat{w}}_{k-1}|{|}^2+{\eta }^2||{\hat{x}}_i|{|}^2$$

---

（9） 最后，将$||{\hat{x}}_i||$看作是R的下限，得到：
$$||{\hat{w}}_{k-1}|{|}^2+2\cdot {\hat{w}}_{k-1}\cdot \eta y_i{\hat{x}}_i+{\eta }^2||{\hat{x}}_i|{|}^2\le ||{\hat{w}}_{k-1}|{|}^2+{\eta }^2||{\hat{x}}_i|{|}^2\le ||{\hat{w}}_{k-1}|{|}^2+{\eta }^2{R}^2$$
仿造分步证明2（6）中的推广，得到
$$||{\hat{w}}_{k-1}|{|}^2+{\eta }^2{R}^2\le ||{\hat{w}}_0|{|}^2+k\cdot {\eta }^2{R}^2$$
最后，整理（7）（9）得：

$$\ast \ast \ast \ast \ast \ast ||{\hat{w}}_k|{|}^2\le k{\eta }^2{R}^2（公式4）\ast \ast \ast \ast \ast \ast$$

 

分步证明4

---

由公式3 “ ${\hat{w}}_k\cdot {\hat{w}}_{opt}\ge k\cdot \eta \gamma$ ”，
和公式4 “ $||{\hat{w}}_k|{|}^2\le k{\eta }^2{R}^2$ ”，得：
$$k\eta \gamma \le {\hat{w}}_k\cdot {\hat{w}}_{opt}\le ||{\hat{w}}_k||\cdot ||{\hat{w}}_{opt}||\le \sqrt{k}\eta R（||{\hat{w}}_{opt}||=1，左边用公式3，右边用公式4）$$
由不等式最左边与最右边 “ $k\eta \gamma \le \sqrt{k}\eta R$ ” 两边同时平方化简得：
$$k^2\gamma \le k{R}^2$$
移下字母得：

$$\ast \ast \ast \ast \ast \ast k\le (\frac{R}{\gamma }{)}^2（证毕）\ast \ast \ast \ast \ast \ast$$

定理表明，误分类的次数k是有上界的，经过有限次搜索可以找到将训练数据完全正确分开的分离超平面。
当训练集线性不可分时，感知机学习算法不收敛，迭代结果会发生震荡。

*公式3和公式4的意义：
公式3： ${\hat{w}}_k\cdot {\hat{w}}_{opt}\ge k\cdot \eta \gamma$ ，说明 ${\hat{w}}_k$ 随k的变大，下界变大
公式4 “ $||{\hat{w}}_k|{|}^2\le k{\eta }^2{R}^2$ ”，说明${\hat{w}}_k$的绝对值有上界
公式3+公式4的几何意义，${\hat{w}}_k$向量通过旋转越来越接近${\hat{w}}_{opt}$向量
 
 

---

（三）感知机学习算法的对偶（等效）形式[2.3.3]

对偶形式对于原始形式最大的不同在于，对偶形式多给了 不同的点不同权重 ，而且对于计算机来说，计算量更小。
（因为在超平面附近的点是最容易误分类的，所以给这些点高权重，可以更快收敛）

在原始形式中：
$$\begin{gathered} w\leftarrow w+\eta y_i{x}_i \\ b\leftarrow b+\eta y_i \end{gathered}$$
那么把上面的递推式子整合（对全部的n个点），得到：
$$\begin{gathered} w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i \\ b=\sum _{i=1}^N{\alpha }_i{y}_i \end{gathered}$$
上式中的 “ ${\alpha }_i=n_i\eta$” ，
$\eta$是递推式子中本来就有的，
$n_i$其实就是个计数（出现几次就是几）的变量，那个点出现的次数越多，就代表着那个点离超平面越近，$n_i$代表的权重越大。

---

这里把原始形式的经验损失函数摆上来：$$L(w,b)=-\sum _{x_iϵM}{y}_i(w\cdot x+b)\ge 0$$
把上面w的整合式代入，得：$$-\sum _{x_iϵM}{y}_i(\sum _{i=1}^N{\alpha }_i{y}_i{x}_i\cdot x+b)\ge 0$$
去负号：$$\sum _{x_iϵM}{y}_i(\sum _{i=1}^N{\alpha }_i{y}_i{x}_i\cdot x+b)\le 0$$
这时，在原始形式中更新w和b，就变成了更新${\alpha }_i$和b，即：
$$\begin{gathered} {\alpha }_i\leftarrow {\alpha }_i+\eta （就是计数器的意思） \\ b\leftarrow b+\eta y_i \end{gathered}$$
 
 

补充，书中的Gram矩阵

Gram矩阵，用来储存不同向量的内积
比如有x₁，x₂，x₃，三个向量，那么Gram矩阵表示为

x1·x1	x1·x2	x1·x3
x2·x1	x2·x2	x2·x3
x3·x1	x3·x2	x3·x3

 
例子：x₁=(3,3)^T，x₂=(4,3)^T，x₃=(1,1)^T，它们生成的Gram矩阵为：

 

---

第二章结束… …
 
链接：[ 全文章目录 ]