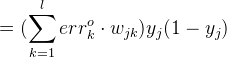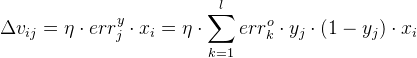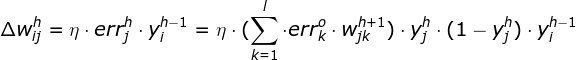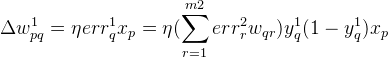深度学习 --- BP算法详解(误差反向传播算法)
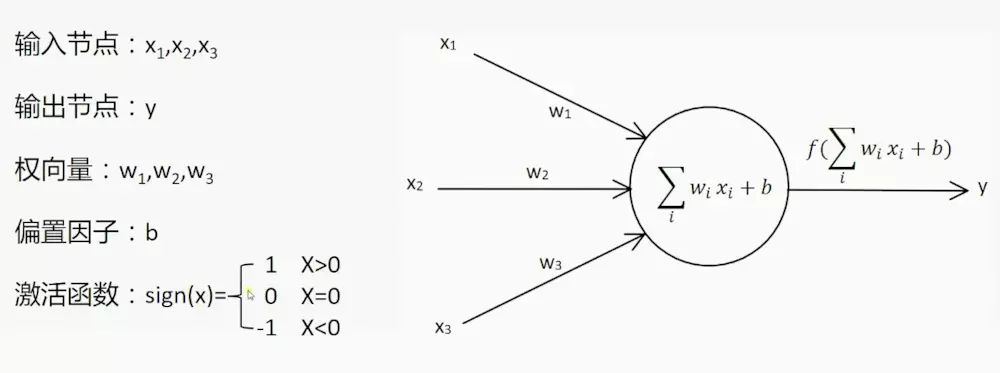
本节开始深度学习的第一个算法BP算法,本打算第一个算法为单层感知器,但是感觉太简单了,不懂得找本书看看就会了,这里简要的介绍一下单层感知器:
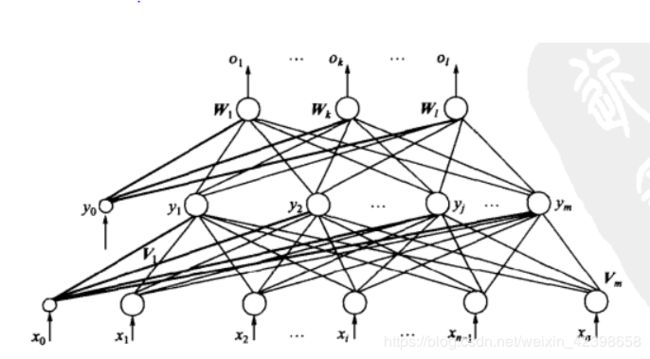
图中可以看到,单层感知器很简单,其实本质上他就是线性分类器,和机器学习中的多元线性回归的表达式差不多,因此它具有多元线性回归的优点和缺点。单层感知器只能对线性问题具有很好的解决能力,但是非线性问题就无法解决了,但是多层感知器却可以解决非线性问题,多层感知器存在的问题是隐层的权值向量无法调整,我们从学习规则来看:
如上图的多层感知器的模型,而单层感知器的通用学习规则为:![]() ,权值的调整量只取决于期望输出和实际输出之差,然而对于隐层节点来说不存在期望输出,因而该权值更新不适合隐层,因为这个问题,一直没有很好的解决办法,所以神经网络停滞了。直到1986年, Rumelhart和McCelland提出了反向传播误差算法即BP,彻底的解决了这个问题,也因此神经神经网络从新回到人们的视野。下面我们详细讲解BP算法,搞懂BP的来龙去脉。
,权值的调整量只取决于期望输出和实际输出之差,然而对于隐层节点来说不存在期望输出,因而该权值更新不适合隐层,因为这个问题,一直没有很好的解决办法,所以神经网络停滞了。直到1986年, Rumelhart和McCelland提出了反向传播误差算法即BP,彻底的解决了这个问题,也因此神经神经网络从新回到人们的视野。下面我们详细讲解BP算法,搞懂BP的来龙去脉。
BP算法
本篇的核心就是BP算法,讲解过程中会有大量的数学公式,想深入理解BP算法的同学,请不要惧怕数学,你要克服它,尝试理解他,数学公式会告诉你最本质的问题,大家跟着我的思路走一定可以理解的,尤其我当时第一次学习时的疑惑的地方更会详细的讲解,同时本篇我是站在对BP一无所知的同学的角度进行讲解,学习过程中,建议大家不要只看,自己也动手推一下,搞懂每个公式的来由,另外就是公式有点繁琐,我会尽量讲清楚,好下面开始:
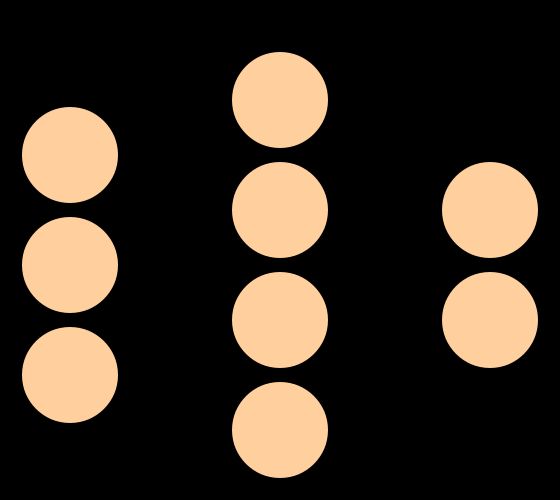
为了简单起见,本篇将以三层感知器为例进行讲解,下面开始:
上图给出了三层感知器的模型图,其中
输入向量为:
![]() ,其中
,其中![]() 为隐层神经元引入阈值而设定的。
为隐层神经元引入阈值而设定的。
隐层输出向量为:
![]() ,其中
,其中![]() 是为输出层神经元引入阈值而设定的。
是为输出层神经元引入阈值而设定的。
输出层向量为:
![]()
期望输出向量为:
![]()
输入层到隐层之间的权值矩阵用![]() 表示:
表示:
![]() ,其中列向量
,其中列向量![]() 为隐层第
为隐层第![]() 个神经元对应的权向量
个神经元对应的权向量
隐层到输出层之间的权值矩阵用![]() 表示为:
表示为:
![]() ,其中列向量
,其中列向量![]() 为输出层第k个神经元对应的权值向量
为输出层第k个神经元对应的权值向量
好,到这里,基本上就是介绍了一些符合的意义,这里大家需要注意的是下标的含义,输入向量使用下表i代表第i个输入。隐层输出向量使用下标j表示第j个隐层输出,而输出层使用下标k表示第k个输出,还有就是这都是向量不是矩阵,只有一列为向量。
我们再看看权值,这些权值组成的是矩阵,为什么是矩阵呢?先看看输入层到隐层的权值矩阵V,其中他是nxm的即n行m列,其中列向量![]() 为隐层第
为隐层第![]() 个神经元对应的权向量,说明v矩阵的列向量对应着隐层的神经元,那么对应的行向量就是代表所有输入向量对隐层的权值,因为隐层的每个神经元的输入是所有的输入向量,这里大家特别注意,隐层权值是矩阵而不是向量,如上图。同理隐层到输出层的权值也矩阵,同时大家要多留意下标代表的意义,下面开始看看他们的数学关系:
个神经元对应的权向量,说明v矩阵的列向量对应着隐层的神经元,那么对应的行向量就是代表所有输入向量对隐层的权值,因为隐层的每个神经元的输入是所有的输入向量,这里大家特别注意,隐层权值是矩阵而不是向量,如上图。同理隐层到输出层的权值也矩阵,同时大家要多留意下标代表的意义,下面开始看看他们的数学关系:
对于输出层,有:
![]()
![]() (不是i,是L的小写)
(不是i,是L的小写) ![]()
对于隐层,有:
![]()
![]()
![]()
上面两式的转移函数![]() 都是单极性Sigmoid函数:
都是单极性Sigmoid函数:
![]()
![]()
这里也要多注意替换思路和下标,理解下标的意义 ,搞明白思路,下面就介绍误差到底是怎么反向传播的。
BP学习算法:
在推倒公式前,我先使用语言简单的描述一下BP的工作过程,这样再看推倒也不至于太突兀,心里有个思路会清晰很多。
BP算法的基本思想是,学习过程由信号的正向传播与误差反向传播两个过程组成。正向传播时,输入样本从输入层传入,经过各隐层逐层处理后,传向输出层。若输出层的实际输出与期望输出不符,则转入误差的反向传播阶段。误差反向传播是将输出误差以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层的误差信号,此误差信号即作为修正单元权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程周而复始的进行,权值不断调整的过程,也就是网络学习训练的过程,此过程一直进行到网络输出的误差减少到可接受的程度,或进行到预先设定的学习次数为止。
大家看了是不是有点晕晕的呢,还是不知道到底如何反向传播的,别急,我们下面通过数学进行说明他到底是如何进行反向传播的。
我么知道误差E的来源就是实际输出和期望输出的差值即:
根据![]() 式将误差E式展开到隐层为:
式将误差E式展开到隐层为:
根据![]() 式将误差E进一步展开至输入层为:
式将误差E进一步展开至输入层为:
到此我们把误差的表达式都带进去了,我们发现权值w和v都在其中,只要w和v取合适的值就可以使E达到最小,此时的公式即为代价函数或者损失误差函数,那么我们怎么求最优值呢?如果大家机器学习学的比较深入,机会想到使用梯度下降法进行更新权值可以达到最优,那什么是梯度呢?什么又是梯度下降呢?为什么梯度下降就是函数下降最快的方向呢?不懂的请看我的这篇文章,请务必深入理解我提的问题,这里就不详细讲了,那篇文体我讲的很透彻了,这里就默认大家都深入理解了梯度下降的概念,我们更新权值只需按照梯度下降方向进行更新即可找到最优的权值。
我们知道一点的梯度就是这里的一阶偏导,因此对w和v求偏导即可:
对输出层的权值调整量:
对隐层的权值调整量:
负号表示梯度下降,![]() 为学习系数,从这里可以看出BP的学习规则是
为学习系数,从这里可以看出BP的学习规则是![]() 类型的,不懂的请看我的深度学习第一篇文章,好,到这里我们基本知道是通过什么进行学习的,但是具体的更新过程还是不知道,我们下面的精力是推倒误差对权值的偏导公式,等推倒 完以后大家也就知道,权值是如何更新的,同时也明白误差反向传播的原理是是什么,下面开始:
类型的,不懂的请看我的深度学习第一篇文章,好,到这里我们基本知道是通过什么进行学习的,但是具体的更新过程还是不知道,我们下面的精力是推倒误差对权值的偏导公式,等推倒 完以后大家也就知道,权值是如何更新的,同时也明白误差反向传播的原理是是什么,下面开始:
推倒之前大家需要明确下标的意思:
输入层向量元素是使用![]() 进行表示的,下标是
进行表示的,下标是![]() ,同时下标的取值范围为:
,同时下标的取值范围为:![]()
隐藏层输出向量元素使用![]() 进行表示,下标是
进行表示,下标是![]() ,同时下标的取值范围为:
,同时下标的取值范围为:![]() (注意,不从0开始,原因看图)
(注意,不从0开始,原因看图)
输入层到隐藏层的权值矩阵元素使用![]() 表示,下标
表示,下标![]() 代表是
代表是![]() 行
行![]() 列的元素,因为是矩阵,所以列对应隐藏层的神经元个数,行代表输入层的个数,所以
列的元素,因为是矩阵,所以列对应隐藏层的神经元个数,行代表输入层的个数,所以![]() ,
,![]()
输出层的输出向量元素使用![]() 表示,下标是k,同时下标的取值范围为:
表示,下标是k,同时下标的取值范围为:![]()
隐藏层到输出层的权值矩阵元素使用![]() 进行表示,下标
进行表示,下标![]() 代表的是
代表的是![]() 行
行![]() 列的元素,因为是矩阵,所以列代表的是输出层神经元的个数,行代表隐藏层的神经元的个数,所以
列的元素,因为是矩阵,所以列代表的是输出层神经元的个数,行代表隐藏层的神经元的个数,所以![]() ,
,![]()
请大家一定要搞明白字母和下标代表的含义,这是深入理解的前提,下面开始推倒公式:
对于输出层,根据![]() 式可得:
式可得:
对于隐层,根据![]() 式可得:
式可得:
为了看起来方便,我们对输出层和隐层各定义一个误差信号![]() :
:
根据![]() 、
、![]() 、
、![]() 输出层权值向量的调整可写为:
输出层权值向量的调整可写为:
![]()
![]()
根据![]() 、
、![]() 、
、![]() 隐藏层权值向量的调整可写为:
隐藏层权值向量的调整可写为:
![]()
![]()
通过 ![]() 、
、 ![]() 可以看到,我们只需要求出err就可以求出最后的权值调整量,下面就开始求解err:
可以看到,我们只需要求出err就可以求出最后的权值调整量,下面就开始求解err:
对于输出层,根据![]() 、
、![]() 使用链式求导规则:
使用链式求导规则:
对于隐藏层,根据![]() ,
,![]() 使用链式求导规则:
使用链式求导规则:
下面就是求![]() ,
,![]() 式中的偏导:
式中的偏导:
对于输出层,此时根据![]() 可得:
可得:
对于输出层,此时根据![]() 可得:
可得:
将 ![]() 、
、![]() 分别代入
分别代入 ![]() 、
、![]() ,同时根据
,同时根据 ![]() 式的:
式的:
根据![]() 、
、![]() 代入权值调整公式即
代入权值调整公式即![]() 、
、![]() :
:
![]()
![]()
我们就得到了三层感知器的权值调整表达式,从上式我们可以看到输出层和隐藏层的权值调节过程,调节过程和三个因素有关即:学习率![]() ,本层输出的误差信号err以及本层的输入信号x或y,其中输出层的误差信号与网络的期望输出和实际输出之差有关,直接反映了输出误差,而隐层的误差信号与前面各层的误差信号均有关,且是从输出层反向传过来的,大家详细的看看
,本层输出的误差信号err以及本层的输入信号x或y,其中输出层的误差信号与网络的期望输出和实际输出之差有关,直接反映了输出误差,而隐层的误差信号与前面各层的误差信号均有关,且是从输出层反向传过来的,大家详细的看看![]() 、
、![]() 两式,会发现输出层的权值调整是期望和真实信号的差值,乘上学习率
两式,会发现输出层的权值调整是期望和真实信号的差值,乘上学习率![]() 和输出层的输入信号(此时就是隐层的输出信号),对于隐藏层的权值调整不仅和当前隐层的输出信号有关,还和输出层的误差信号有关,如果是多个隐层,那么隐层的信号都会和输出层的误差信号err有关,也就是说是通过输出层的误差信号err反向传播到各层,对于多隐层的神经网络的误差信号传播是不是这样呢?我们在根据上面三层网络推倒到多隐层的网络。
和输出层的输入信号(此时就是隐层的输出信号),对于隐藏层的权值调整不仅和当前隐层的输出信号有关,还和输出层的误差信号有关,如果是多个隐层,那么隐层的信号都会和输出层的误差信号err有关,也就是说是通过输出层的误差信号err反向传播到各层,对于多隐层的神经网络的误差信号传播是不是这样呢?我们在根据上面三层网络推倒到多隐层的网络。
对于一般多层感知器,设有h个隐层,按照前行顺序,各隐层的节点数分别为记为![]() 各隐层的输出分别为计为
各隐层的输出分别为计为![]() ,各层权值矩阵分别记为
,各层权值矩阵分别记为![]() ,则各层的权值调整公式为:
,则各层的权值调整公式为:
输出层:
![]()
![]()
![]()
![]()
第h隐层:
![]() ;
; ![]()
按照上面的规律,第一层的隐藏层的权值调整为:
![]()
![]()
此时大家应该好好理解一下上式的公式,深入理解他是怎么反向传播的,这个反向表现在哪里?在这里简单的解释一下,对于隐层,根据![]() 式,我们可以看到隐层的权值更新和输出层的误差和上一层的权值的乘积有关,这就是反向的来意,所有隐层的权值调整都和输出层的误差有关,也就是说所有权值的调整都来源与输出层的期望值和真实值的差有关,这就是反向传播的来历,后面会使用图来解释这方面的内容,下面先把
式,我们可以看到隐层的权值更新和输出层的误差和上一层的权值的乘积有关,这就是反向的来意,所有隐层的权值调整都和输出层的误差有关,也就是说所有权值的调整都来源与输出层的期望值和真实值的差有关,这就是反向传播的来历,后面会使用图来解释这方面的内容,下面先把![]() 、
、![]() 式使用向量进行表示一下:
式使用向量进行表示一下:
对于输出层;
设![]() ,
,![]() 则:
则:
![]()
对于隐层:
设![]() ,
,![]() 则:
则:
![]()
到这里公式就推倒结束了,下面详细看看他到底如何反向传播的,这里给出误差信号流向图进行解释:
这里只画出了输出层和第一层隐藏层,是完全按照公式 ![]() 、
、![]() 来的,大家结合者这两个公式好好理解一下,反向误差的传播也很清晰d-o一直反向调节权值,这就是反向的来源,请大家务必深入理解,有什么疑问请留言,本节到此结束,下一节我们看看BP有哪些性质以及优缺点,如何改进等。
来的,大家结合者这两个公式好好理解一下,反向误差的传播也很清晰d-o一直反向调节权值,这就是反向的来源,请大家务必深入理解,有什么疑问请留言,本节到此结束,下一节我们看看BP有哪些性质以及优缺点,如何改进等。
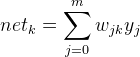
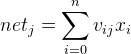
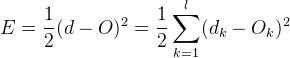
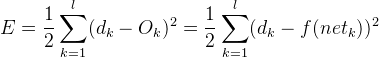
![= \frac{1}{2}\sum_{k=1}^{l}[d_k-f(\sum_{j=0}^{m}w_{jk}y_j)]^2](http://img.e-com-net.com/image/info8/bac2348109ca4f0f91db1cb0ea34d543.gif)
![E= \frac{1}{2}\sum_{k=1}^{l}\left \{ \right.d_k-f[\sum_{j=0}^{m}w_{jk}f(ne)]\left. \right \}^2](http://img.e-com-net.com/image/info8/7e3cbfe7ec0e4499a0328294d5355437.gif)
![= \frac{1}{2}\sum_{k=1}^{l}\left \{ \right.d_k-f[\sum_{j=0}^{m}w_{jk}f(\sum_{i=0}^{n}v_{ij}x_i)]\left. \right \}^2](http://img.e-com-net.com/image/info8/23a0cefea5df49509b094db04b8fa540.gif)
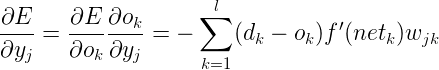
![err_j^y= - \frac{\partial E}{\partial y_j}f'(net_j)=[\sum_{k=1}^{l}(d_k-o_k)f'(net_j)w_{jk}]f'(net_j)](http://img.e-com-net.com/image/info8/e4570091abc64ef7b5fc9345f4e4cc33.gif)