统计推断-经典统计推断
统计推断-经典统计推断
- 基本问题
- 统计学与概率论
- 贝叶斯统计与经典统计
- 推断模型与推断变量
- 术语解释
- 经典参数估计
- 术语
- 最大似然估计
- 均值和方差的估计
- 置信区间
- 求近似的置信区间
- 基于方差近似估计量的置信区间
- 线性回归
- 最小二乘法合理性
- 贝叶斯线性回归
- 多元线性回归
- 非线性回归
- 线性规划注意事项
- 简单假设检验
- 内曼-皮尔逊引理
- 显著性检验
- 广义似然比和拟合优度检验
基本问题
- 统计推断是什么?
统计推断是从观测数据推断未知变量或未知模型的有关信息的过程。 - 统计推断的用途是什么?
统计推断可用于“参数估计”,“假设检验”,“显著性检验” - 统计推断的研究思路是什么?
主要有两种思路:“贝叶斯统计推断” 和“经典统计推断”。(大局方法) - 统计推断具体使用的"算法"有哪些?
最大后验概率准则,最小均方估计,最大似然估计,回归,似然比检验等。(小方法)
统计学与概率论
“统计学”与“概率论”在认识论上有明显的区别。
概率论是建立在概率公理上的系统自我完善的数学课题。我们会假设一个完整的特定的概率模型满足概率公理,然后用数学方法研究模型的一些性质。概率模型无需与现实世界相一致,它值对概率公理负责。
统计学是针对一个具体的问题,寻求合理的研究方法,希望得到合理的结论。这就存在很大的自由度,采取不同的研究方法,结论可能不同。通常我们会附加一些限制条件,以便得到“理想结论”。
正是由于统计学的这种特征,现实社会存在许多人为制造的"理想结论",这些结论可能来源于真实的数据,但研究方法是人为选定的。
贝叶斯统计与经典统计
贝叶斯统计与经典统计(频率学派)是两种突出但对立的思想学派。
最重要的区别就是如何看待未知模型或变量。贝叶斯学派将其看成已知分布的随机变量。而经典统计将其看成未知的待估计的量。
贝叶斯方法将统计拉回“概率论”的研究领域,使得每个问题只有一个答案。经典统计将未知量看作一种参数,它是一个常数,未知需要估计。
从现实角度来看,贝叶斯统计主张将假设的先验分布公开,即研究过程公开了。贝叶斯统计推断涉及到多维度积分,计算困难,所以贝叶斯学派的最新成功可能集中于如何计算上。
推断模型与推断变量
这两种问题有细微的区别。推断模型是为了研究某种现象或过程的一般规律,以期能够预测未来现象的结果。推断变量是从已知的量,推测未知的量,例如从gps信息推断所处于的位置。
术语解释
- 参数估计:对参数进行估计,使得在某种概率意义下估计接近真实值。
- 假设检验:未知参数根据对立的假设可能取有限个值,选择一个假设,目标是使犯错误的概率最小。
- 显著性检验:对于一个给定的假设,希望发生错误(“接受错误”与“拒绝正确”)的概率适当地小.
- 最大似然估计:在选择参数 θ \theta θ时,使得观测数据最有可能出现,即观测到当前数据的概率达到最大。
- 线性回归:对于给定的一组观测数据,采用线性拟合的方式建立模型。约束条件是使观测数据与模型值的差的平方和最小。(最小二乘法)
- 似然比检验:对于给定的两个假设,根据他们发生的可能性的比值选择其中一个,使得犯错的概率适当小。
经典参数估计
虽然把 θ \theta θ当作常数,而不是随机变量,但仍然把 θ \theta θ估计量当作随机变量 Θ ^ \hat\Theta Θ^,因为 θ ^ \hat\theta θ^一般而言是 x x x的函数, θ ^ = g ( x ) \hat\theta=g(x) θ^=g(x),所以也有: Θ ^ = g ( X ) \hat\Theta=g(X) Θ^=g(X)。也可以写成 Θ ^ = g ( X ; θ ) \hat\Theta=g(X;\theta) Θ^=g(X;θ),这个式子的意思是 Θ ^ \hat\Theta Θ^是 θ \theta θ的数值函数。
术语
Θ ^ n \hat\Theta_n Θ^n是未知参数 θ \theta θ的估计量,也即 n n n个观测 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn( X X X的分布依赖于 θ \theta θ)的函数:
- 估计误差: Θ ~ n = Θ ^ n − θ \tilde \Theta_n=\hat\Theta_n-\theta Θ~n=Θ^n−θ
- 估计量偏差: b θ ( Θ ^ n ) = E ( Θ ^ ) − θ b_\theta(\hat\Theta_n)=E(\hat\Theta)-\theta bθ(Θ^n)=E(Θ^)−θ
- 估计量的偏差,方差,期望是\theta的函数,而估计误差是 ( X 1 , X 2 , . . . . , X n , θ ) (X_1,X_2,....,X_n,\theta) (X1,X2,....,Xn,θ)的函数
- 无偏估计的定义:如果 E ( Θ ^ ) = θ E(\hat\Theta)=\theta E(Θ^)=θ对 θ \theta θ所有可能的取值都成立
- 渐进无偏的定义:如果 lim n → ∞ E ( Θ ^ n ) = θ \lim _{n\rightarrow \infty}{E(\hat\Theta_n)}=\theta limn→∞E(Θ^n)=θ.
- 称 Θ ^ \hat\Theta Θ^是 θ \theta θ的相合估计序列,如果对于所有的 θ \theta θ可能的取值, Θ ^ \hat\Theta Θ^依概率收敛到参数 θ \theta θ的真值: ∀ ϵ > 0 , lim n → ∞ P ( ∣ Θ ^ − θ ∣ > ϵ ) = 0. \forall \epsilon >0,\lim _{n\rightarrow \infty}{P(|\hat\Theta - \theta|>\epsilon)=0.} ∀ϵ>0,limn→∞P(∣Θ^−θ∣>ϵ)=0.
- E ( Θ ~ 2 ) = E [ ( Θ ^ n − θ ) 2 ] = v a r ( Θ ^ n − θ ) + E 2 ( Θ ^ n − θ ) = v a r ( Θ ^ n ) + b θ 2 ( Θ ^ ) E(\tilde\Theta ^2)=E[(\hat\Theta_n-\theta)^2]=var(\hat\Theta_n-\theta)+E^2(\hat\Theta_n-\theta)=var(\hat\Theta_n)+b^2 _\theta(\hat\Theta) E(Θ~2)=E[(Θ^n−θ)2]=var(Θ^n−θ)+E2(Θ^n−θ)=var(Θ^n)+bθ2(Θ^),这个式子建立了估计均方误差、估计量方差、估计偏差的关系。可以看出均方误差也是 θ \theta θ的函数。如果均方误差不变,则减小方差会增大偏差,减小偏差会增大方差。
最大似然估计
定义:设观测向量 X = ( X 1 , X 2 , . . . , X n ) X=(X_1,X_2,...,X_n) X=(X1,X2,...,Xn)的联合分布列为 p X 1 , X 2 , . . , X n ( x 1 , x 2 , . . . , x n ; θ ) = p X ( x 1 , x 2 , . . . , x n ; θ ) p_{X_1,X_2,..,X_n}(x_1,x_2,...,x_n;\theta)=p_{X}(x_1,x_2,...,x_n;\theta) pX1,X2,..,Xn(x1,x2,...,xn;θ)=pX(x1,x2,...,xn;θ),最大似然估计就是寻求参数 θ = θ ^ \theta=\hat\theta θ=θ^使得关于 θ \theta θ的函数 p X ( x 1 , x 2 , . . . , x n ; θ ) p_{X}(x_1,x_2,...,x_n;\theta) pX(x1,x2,...,xn;θ)达到最大,即寻求参数 θ = θ ^ \theta=\hat\theta θ=θ^使得观测值 X X X最有可能出现。
当 X X X为连续随机变量时, p X p_X pX用概率密度函数 f X ( x 1 , x 2 , . . . , x n ; θ ) f_X(x_1,x_2,...,x_n;\theta) fX(x1,x2,...,xn;θ)代替。
如果 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn是相互独立的,那么 p X = p X 1 p X 2 . . . p X n , p_X=p_{X_1}p_{X_2}...p_{X_n}, pX=pX1pX2...pXn,此时可用对数似然函数来简化计算: l n ( p X ) = l n p X 1 + . . . + l n p X n ln(p_X)=lnp_{X_1}+...+lnp_{X_n} ln(pX)=lnpX1+...+lnpXn
与贝叶斯最大后验概率准则对比:
最大后验概率准则:求 θ = θ ^ \theta=\hat\theta θ=θ^使得 p Θ ( θ ) p X ∣ Θ ( x ∣ θ ) p_\Theta( \theta)p_{X|\Theta}(x|\theta) pΘ(θ)pX∣Θ(x∣θ)取最大值。
最大似然估计:求 θ = θ ^ \theta=\hat\theta θ=θ^使得 p X ( X ; θ ) p_{X}(X;\theta) pX(X;θ)取最大值。
可以看出当 Θ \Theta Θ是均匀分布时,最大后验准则等价于最大似然估计。均匀分布即 Θ \Theta Θ取任何值的概率都相等,这就是经典统计推断与贝叶斯统计推断的不同之处。
如果 θ \theta θ的最大似然估计是 θ ^ \hat\theta θ^,那么 g ( θ ) g(\theta) g(θ)的最大似然估计是 g ( θ ^ ) g(\hat\theta) g(θ^).这里要求 g ( x ) g(x) g(x)是一一映射函数。
举例:某人上班迟到时间是一个随机变量X,服从参数为 [ 0 , θ ] [0,\theta] [0,θ]上的均匀分布, θ \theta θ未知,是随机变量 Θ \Theta Θ的一个值, Θ \Theta Θ服从 [ 0 , 1 ] [0,1] [0,1]上的均匀分布。假设某次迟到时间为x。用最大似然估计来估计 θ \theta θ。
流程:
f X ( x ; θ ) = 1 θ f_X(x;\theta)=\frac{1} {\theta} fX(x;θ)=θ1
画出 θ − x \theta-x θ−x的取值范围图:

θ \theta θ的取值范围图中阴影部分。对于观测值 x = x 0 , θ x=x_0,\theta x=x0,θ的取值范围为图中红线部分。显然当 θ = x \theta =x θ=x时能使 f X f_X fX达到最大。所以 θ \theta θ的最大似然估计 Θ ^ = X \hat\Theta=X Θ^=X.
均值和方差的估计
利用经典统计推断一个概率分布的均值和方差(不一定是“最大似然估计”)。
这里的目标是通过样本推断总体的无偏估计均值和方差。
假设条件:
- 观测向量 ( X 1 , X 2 , . . . , X n ) (X_1,X_2,...,X_n) (X1,X2,...,Xn)是独立同分布
- 均值为未知参数 θ \theta θ.方差为未知参数 v = σ 2 v=\sigma^2 v=σ2
对于均值最自然的估计量是样本均值:
Θ ^ = M n = X 1 + X 2 + . . . + X n n \hat\Theta=M_n=\frac{X_1+X_2+...+X_n}{n} Θ^=Mn=nX1+X2+...+Xn
样本均值当作均值估计量时有:
- E ( M n ) = θ E(M_n)=\theta E(Mn)=θ,所以 M n M_n Mn是 θ \theta θ的无偏估计量。
- E ( X i M n ) = θ 2 = E ( X i ) E ( M n ) E(X_iM_n)=\theta^2=E(X_i)E(M_n) E(XiMn)=θ2=E(Xi)E(Mn),所以 M n M_n Mn和 X i X_i Xi不相关。
- v a r ( M n ) = v a r ( X 1 + X 2 + . . . + X n ) / n 2 = v / n var(M_n)=var(X_1+X_2+...+X_n)/n^2=v/n var(Mn)=var(X1+X2+...+Xn)/n2=v/n.可见方差和均方不依赖
- 均方误差 E [ ( Θ ^ − θ ) 2 ] = E [ ( M n − θ ) 2 ] = E [ ( M n − E ( M n ) ) 2 ] = v a r ( M n ) E[(\hat\Theta-\theta)^2]=E[(M_n-\theta)^2]=E[(M_n-E(M_n))^2]=var(M_n) E[(Θ^−θ)2]=E[(Mn−θ)2]=E[(Mn−E(Mn))2]=var(Mn),对于无偏估计量总有方差等于均方误差。上式也说明估计量 M n M_n Mn的方差和均方误差都不依赖于 θ \theta θ(不是所有的估计量都有这个性质).
- 样本均值 M n M_n Mn不一定是方差最小的估计量。例如取 Θ ^ = 0 \hat\Theta=0 Θ^=0,此时方差是0,由于“均方误差=方差+偏差的平方”,此时偏差不是0,均方误差也依赖于 θ \theta θ了。
对于方差 v v v的估计量最自然的选择:
V ^ = 1 n ∑ i = 1 n ( X i − M n ) 2 = S ‾ n 2 \hat V=\frac{1}{n}\sum _{i=1}^{n}(X_i-M_n)^2=\overline S_n^2 V^=n1i=1∑n(Xi−Mn)2=Sn2
那么 S ‾ n 2 \overline S_n^2 Sn2是否是 v v v的无偏估计量呢?
E ( V ^ ) = E ( S ‾ n 2 ) = 1 n ∑ i = 1 n [ E ( X i 2 ) − 2 E ( X i M n ) + E ( M n 2 ) ] = 1 n [ n ( v + θ 2 ) − v − n θ 2 ] = v − v n = n − 1 n v E(\hat V)=E(\overline S_n^2)=\frac{1}{n} \sum_{i=1}^{n}[E(X_i^2)-2E(X_iM_n)+E(M_n^2)]\\=\frac{1}{n}[n(v+\theta^2)-v-n\theta^2]\\=v-\frac{v}{n}=\frac{n-1}{n}v E(V^)=E(Sn2)=n1∑i=1n[E(Xi2)−2E(XiMn)+E(Mn2)]=n1[n(v+θ2)−v−nθ2]=v−nv=nn−1v
说明 S ‾ 2 \overline S^2 S2不是 v v v的无偏估计量,比方差 v v v少 v / n v/n v/n,但 S ‾ 2 \overline S^2 S2是渐进无偏的.为了得到 v v v的无偏估计量,可以对 S ‾ 2 \overline S^2 S2进行一定的缩放:
E ( S ^ n 2 ) = E [ n n − 1 ∗ S ‾ n 2 ] = v E(\hat S_n^2)=E[\frac{n}{n-1}*\overline S_n^2]=v E(S^n2)=E[n−1n∗Sn2]=v
所以方差的估计量有两个:
S ‾ 2 = 1 n ∑ i = 1 n ( X i − M n ) 2 , S ^ 2 = 1 n − 1 ∑ i = 1 n ( X i − M n ) 2 \overline S^2=\frac{1}{n}\sum _{i=1}^{n}(X_i-M_n)^2,\hat S^2=\frac{1}{n-1}\sum _{i=1}^{n}(X_i-M_n)^2 S2=n1i=1∑n(Xi−Mn)2,S^2=n−11i=1∑n(Xi−Mn)2
无偏估计方差为什么会出现有(n-1)?
方差的计算式子中 E [ ( X − μ ) 2 ] E[(X-\mu)^2] E[(X−μ)2]中 μ \mu μ是常数,方差为0.而在这里的估计过程中,期望和方差都是待估计量,都不是常数。所以样本的方差 S ‾ n 2 \overline S_n^2 Sn2包含了样本均值的方差 v / n v/n v/n和样本的无偏方差 S ^ n 2 \hat S_n^2 S^n2.
置信区间
粗略地说,置信区间的作用是使用"区间估计"代替“点估计”,使得"区间"包含真值的概率达到适当的水平。这个适当的水平即"置信水平",通常设为 1 − α 1-\alpha 1−α.置信区间设为 [ Θ ^ n − , Θ ^ n + ] [\hat\Theta_n^-,\hat\Theta_n^+] [Θ^n−,Θ^n+],要求置信区间包含真值的概率达到置信水平:
P ( Θ ^ n − ≤ θ ≤ Θ ^ n + ) ≥ ( 1 − α ) P(\hat\Theta_n^- \le \theta \le \hat\Theta_n^+)\ge (1-\alpha) P(Θ^n−≤θ≤Θ^n+)≥(1−α)
称 [ Θ ^ n − , Θ ^ n + ] [\hat\Theta_n^-,\hat\Theta_n^+] [Θ^n−,Θ^n+]为 ( 1 − α ) (1-\alpha) (1−α)置信区间。
请注意,这里随机变量是与区间相关的。例如假设 [ 0 , 1 ] [0,1] [0,1]是 θ \theta θ的 0.95 0.95 0.95置信区间,准确的理解是 [ 0 , 1 ] [0,1] [0,1]包含 θ \theta θ的概率是 0.95 0.95 0.95,而不能说 θ \theta θ落在 [ 0 , 1 ] [0,1] [0,1]内的概率是 0.95 0.95 0.95.
求近似的置信区间
在很多重要的模型中 Θ ^ \hat\Theta Θ^的分布是渐进正态无偏的(中心极限定理),在 n → ∞ n\rightarrow \infty n→∞时, E ( Θ ^ ) → θ E(\hat\Theta) \rightarrow \theta E(Θ^)→θ,所以:
Z n = Θ ^ n − θ v a r ( Θ ^ ) Z_n=\frac{\hat\Theta_n - \theta}{\sqrt{var(\hat\Theta)}} Zn=var(Θ^)Θ^n−θ
服从标准正态分布.
查表 Φ ( 1.96 ) = P ( Z n ≤ 1.96 ) = 0.975 \Phi(1.96)=P(Z_n\le1.96)=0.975 Φ(1.96)=P(Zn≤1.96)=0.975
假设 θ \theta θ处于置信区间的中点,那么 Θ ^ − = Θ ^ − l , Θ ^ + = Θ ^ + l \hat\Theta^-=\hat\Theta-l,\hat\Theta^+=\hat\Theta+l Θ^−=Θ^−l,Θ^+=Θ^+l,于是有:
P ( − l ≤ Θ ^ − θ ≤ + l ) ≥ ( 1 − α ) P(-l \le \hat\Theta-\theta \le +l)\ge (1-\alpha) P(−l≤Θ^−θ≤+l)≥(1−α)
( Θ ^ − θ ) (\hat\Theta-\theta) (Θ^−θ)正态分布的对称轴是0(因为均值为0).
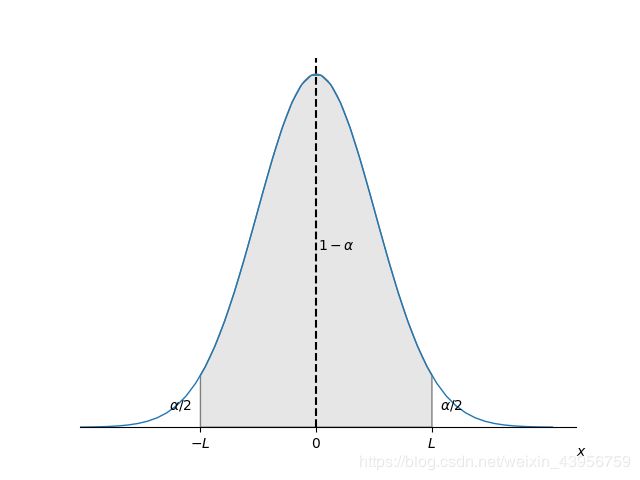
如图阴影部分面积为 ( 1 − α ) (1-\alpha) (1−α),那么就应该有 Φ ( L ) = 1 − α / 2 \Phi(L)=1-\alpha/2 Φ(L)=1−α/2
如果 α = 0.05 \alpha =0.05 α=0.05,置信水平是 0.95 0.95 0.95,查表 Φ ( 1.96 ) = 1 − 0.25 = 0.975 \Phi(1.96)=1-0.25=0.975 Φ(1.96)=1−0.25=0.975,
所以 L = 1.96 = Θ ^ − θ v a r ( Θ ^ ) L=1.96=\frac{\hat\Theta-\theta}{\sqrt{var(\hat\Theta)}} L=1.96=var(Θ^)Θ^−θ,
Θ ^ − L v a r ( Θ ^ ) ≤ θ ≤ Θ ^ + L v a r ( Θ ^ ) \hat\Theta - L\sqrt{var(\hat\Theta)} \le \theta \le \hat\Theta + L\sqrt{var(\hat\Theta)} Θ^−Lvar(Θ^)≤θ≤Θ^+Lvar(Θ^)
其中 Φ ( L ) = 1 − α / 2 \Phi(L)=1-\alpha/2 Φ(L)=1−α/2.上式就是 ( 1 − α ) (1-\alpha) (1−α)置信水平的置信区间。
假设 θ \theta θ是固定的,运用相同的统计过程建立了n个 0.95 0.95 0.95置信区间。可以预期在n个置信区间中,将有95%的置信区间包含 θ \theta θ.
基于方差近似估计量的置信区间
在上面的置信区间式子中包含估计量的方差 v a r ( Θ ^ ) var(\hat\Theta) var(Θ^),如果用样本均值 Θ ^ = M n = X 1 + X 2 + . . . + X n n \hat\Theta=M_n=\frac{X_1+X_2+...+X_n}{n} Θ^=Mn=nX1+X2+...+Xn
来估计 θ \theta θ,用无偏估计量:
S ^ 2 = 1 n − 1 ∑ i = 1 n [ ( X i − θ ) 2 ] \hat S^2=\frac{1}{n-1}\sum _{i=1}^{n}[(X_i-\theta)^2] S^2=n−11i=1∑n[(Xi−θ)2]
来估计方差.那么就可以用 S ^ 2 / n \hat S^2/n S^2/n来估计 v a r ( Θ ^ ) = v a r ( M n ) = v / n var(\hat\Theta)=var(M_n)=v/n var(Θ^)=var(Mn)=v/n。
对于给定的 α \alpha α,可以构造一个近似的 ( 1 − α ) (1-\alpha) (1−α)的置信区间,即:
[ Θ ^ − L S ^ n , Θ ^ + L S ^ n ] [\hat\Theta-L\frac{\hat S}{\sqrt n},\hat\Theta+L\frac{\hat S}{\sqrt n}] [Θ^−LnS^,Θ^+LnS^],
其中 Φ ( L ) = 1 − α / 2 \Phi(L)=1-\alpha/2 Φ(L)=1−α/2.
整个过程有两个近似:
- 将 Θ ^ \hat\Theta Θ^看作正态分布的随机变量
- 用估计 S ^ 2 / n \hat S^2/n S^2/n来代替来 Θ ^ \hat\Theta Θ^真实的方差 v a r ( Θ ^ ) var(\hat\Theta) var(Θ^)
所以这里实际上是用正态分布去近似了一个不是正态分布的概率。为了 Φ ( L ) = 1 − α / 2 \Phi(L)=1-\alpha/2 Φ(L)=1−α/2更精确,用一个比正态分布更好的 t t t-分布去计算 L L L.
现在定义一个随机变量:
T n = Θ ^ S ^ n / n T_n=\frac{\hat\Theta}{\hat S_n /\sqrt n} Tn=S^n/nΘ^
,称 T n T_n Tn为自由度 n − 1 n-1 n−1的 t t t-分布。
此时 L L L的计算式子为:
Ψ n − 1 ( L ) = 1 − α / 2 \Psi_{n-1}(L)=1-\alpha/2 Ψn−1(L)=1−α/2.
其中 Ψ n − 1 ( z ) \Psi_{n-1}(z) Ψn−1(z)是自由度为 n − 1 n-1 n−1的t-分布的概率分布函数.
由t-分布和正态分布的关系,可以得出t-分布应该和正态分布函数的图像近似。
举例:利用电子天平得到一个物体重量的八次测量,观测值是真实的质量加上一个随机误差,随机误差服从 ( 0 , v ) (0,v) (0,v)的正态分布,假设每次观测误差都是相互独立的,观测值如下:
X = ( 0.5547 , 0.5404 , 0.6364 , 0.6438 , 0.4917 , 0.5674 , 0.5664 , 0.6066 ) X=(0.5547,0.5404,0.6364,0.6438,0.4917,0.5674,0.5664,0.6066) X=(0.5547,0.5404,0.6364,0.6438,0.4917,0.5674,0.5664,0.6066)
计算95%置信区间。
这类不知道方差的情况,使用t-分布来近似计算置信区间.
流程:
- 计算均值和方差.
θ = E ( Θ ^ ) = E ( M n ) = 0.574 \theta=E(\hat \Theta)=E(M_n)=0.574 θ=E(Θ^)=E(Mn)=0.574,方差的估计是 S ^ 2 n = 1 n − 1 ∑ i = 1 n [ ( X i − θ ) 2 ] = 3.2952 ∗ 1 0 − 4 \frac{\hat S^2}{n}=\frac{1}{n-1}\sum _{i=1}^{n}[(X_i-\theta)^2]=3.2952*10^{-4} nS^2=n−11∑i=1n[(Xi−θ)2]=3.2952∗10−4
因而标准差估计为: 3.2952 ∗ 1 0 − 4 = 0.0182 \sqrt{3.2952*10^{-4}}=0.0182 3.2952∗10−4=0.0182 - 查t-分布表
查表使得: Ψ 7 ( L ) = 1 − α / 2 = 0.975 = Ψ ( 2.365 ) \Psi_{7}(L)=1-\alpha/2=0.975=\Psi(2.365) Ψ7(L)=1−α/2=0.975=Ψ(2.365) - 计算置信区间 [ Θ ^ − L S ^ n , Θ ^ + L S ^ n ] [\hat\Theta-L\frac{\hat S}{\sqrt n},\hat\Theta+L\frac{\hat S}{\sqrt n}] [Θ^−LnS^,Θ^+LnS^]
置信区间为: [ Θ ^ − 0.043 , Θ ^ + 0.043 ] [\hat\Theta-0.043,\hat\Theta+0.043] [Θ^−0.043,Θ^+0.043].使用样本均值作为 Θ ^ \hat\Theta Θ^的估计则 0.95 0.95 0.95置信区间为: [ 0.531 , 0.617 ] [0.531,0.617] [0.531,0.617]
方差的估计方式可以有多种,所以答案不是唯一的,这里采用的是样本的无偏估计方差 S ^ 2 \hat S^2 S^2。
线性回归
线性回归的典型应用:已知 n n n组数据对 ( x i , y i ) (x_i,y_i) (xi,yi),使用线性回归 y = c x + d y=cx+d y=cx+d来拟合 x , y x,y x,y之间的关系。
用最小二乘法推导计算公式:
{ c x 1 + d = y 1 c x 2 + d = y 2 . . . c x n + d = y n \begin{cases} cx_1+d=y_1 \\ cx_2+d=y_2 \\ ... \\ cx_n+d=y_n \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧cx1+d=y1cx2+d=y2...cxn+d=yn
将此式写成矩阵形式 A z = b Az=b Az=b:
A = ( x 1 1 x 2 1 . . . . . . x n 1 ) , z = ( c d ) , b = ( y 1 y 2 . . . y n ) A=\begin{pmatrix}x_{1} & 1 \\x_2 & 1 \\... & ... \\x_n & 1\end{pmatrix}, z=\begin{pmatrix} c \\ d \end{pmatrix}, b=\begin{pmatrix} y1 \\ y2 \\...\\y_n \end{pmatrix} A=⎝⎜⎜⎛x1x2...xn11...1⎠⎟⎟⎞,z=(cd),b=⎝⎜⎜⎛y1y2...yn⎠⎟⎟⎞
A z = b , A T A z = A T b Az=b,A^TAz=A^Tb Az=b,ATAz=ATb
z = ( A T A ) − 1 A T b z=(A^TA)^{-1}A^Tb z=(ATA)−1ATb
计算:
A T = ( x 1 x 2 . . . x n 1 1 . . . 1 ) A^T=\begin{pmatrix} x_1 & x_2 & ... & x_n \\ 1 & 1 & ... & 1 \end{pmatrix} AT=(x11x21......xn1)
A T A = ( ∑ x i 2 ∑ x i ∑ x i n ) A^TA=\begin{pmatrix} \sum x_i^2 & \sum x_i \\ \sum x_i & n \end{pmatrix} ATA=(∑xi2∑xi∑xin)
由于: ( a b c d ) − 1 = 1 a d − b c ( d − b − c a ) \begin{pmatrix} a & b \\ c& d \end{pmatrix}^{-1}=\frac{1}{ad-bc}\begin{pmatrix} d & -b \\ -c & a \end{pmatrix} (acbd)−1=ad−bc1(d−c−ba)
( A T A ) − 1 = 1 n ∑ x i 2 − ( ∑ x i ) 2 ( n − ∑ x i − ∑ x i ∑ x i 2 ) (A^TA)^{-1}=\frac{1}{n\sum x_i^2-(\sum x_i)^2}\begin{pmatrix} n & -\sum x_i \\ -\sum x_i & \sum x_i^2 \end{pmatrix} (ATA)−1=n∑xi2−(∑xi)21(n−∑xi−∑xi∑xi2)
A T b = ( ∑ ( x i y i ) ∑ y i ) A^Tb=\begin{pmatrix} \sum(x_iy_i) \\ \sum y_i \end{pmatrix} ATb=(∑(xiyi)∑yi)
z = ( A T A ) − 1 A T b = 1 n ∑ x i 2 − ( ∑ x i ) 2 ( n − ∑ x i − ∑ x i ∑ x i 2 ) ( ∑ ( x i y i ) ∑ y i ) z=(A^TA)^{-1}A^Tb=\frac{1}{n\sum x_i^2-(\sum x_i)^2}\begin{pmatrix} n & -\sum x_i \\ -\sum x_i & \sum x_i^2 \end{pmatrix} \begin{pmatrix} \sum(x_iy_i) \\ \sum y_i \end{pmatrix} z=(ATA)−1ATb=n∑xi2−(∑xi)21(n−∑xi−∑xi∑xi2)(∑(xiyi)∑yi)
= 1 n ∑ x i 2 − ( ∑ x i ) 2 ( n ∑ ( x i y i ) − ∑ x i ∑ y i − ∑ x i ∑ ( x i y i ) + ∑ ( x i 2 ) ∑ y i ) =\frac{1}{n\sum x_i^2-(\sum x_i)^2} \begin{pmatrix} n\sum(x_iy_i)-\sum x_i \sum y_i \\ -\sum x_i \sum(x_iy_i)+\sum(x_i^2)\sum y_i \end{pmatrix} =n∑xi2−(∑xi)21(n∑(xiyi)−∑xi∑yi−∑xi∑(xiyi)+∑(xi2)∑yi)
设 n x ‾ = ∑ ( x i ) , n y ‾ = ∑ y i n\overline x=\sum (x_i),n\overline y=\sum y_i nx=∑(xi),ny=∑yi,则有:
∑ x ‾ 2 = 1 / n ∗ ∑ ( x 1 + x 2 + . . . + x n ) y ‾ = ∑ x i x ‾ \sum \overline x^2 =1/n*\sum (x_1+x_2+...+x_n)\overline y=\sum x_i\overline x ∑x2=1/n∗∑(x1+x2+...+xn)y=∑xix
∑ x ‾ y ‾ = ∑ ( x i y ‾ ) = ∑ ( x ‾ y i ) \sum \overline x\overline y=\sum (x_i\overline y)=\sum (\overline x y_i) ∑xy=∑(xiy)=∑(xyi)
推导一个分母:
n ( x 1 2 + x 2 2 + . . . + x n 2 ) − ( x 1 + x 2 + . . . + x n ) 2 = n ( x 1 2 + x 2 2 + . . . + x n 2 ) − ( n x ‾ ) 2 = n [ ( x 1 2 + x 2 2 + . . . + x n 2 ) − n x ‾ 2 ] = n ∑ ( x i 2 − x ‾ 2 ) = n ∑ ( x i 2 − 2 x i x ‾ + x ‾ 2 ) = n ∑ ( x i − x ‾ ) 2 n(x_1^2+x_2^2+...+x_n^2)-(x_1+x_2+...+x_n)^2=n(x_1^2+x_2^2+...+x_n^2)-(n\overline x)^2\\=n[(x_1^2+x_2^2+...+x_n^2)-n\overline x^2]=n\sum (x_i^2-\overline x^2)=n\sum(x_i^2-2x_i\overline x + \overline x^2)\\=n\sum(x_i-\overline x)^2 n(x12+x22+...+xn2)−(x1+x2+...+xn)2=n(x12+x22+...+xn2)−(nx)2=n[(x12+x22+...+xn2)−nx2]=n∑(xi2−x2)=n∑(xi2−2xix+x2)=n∑(xi−x)2
类似的,最终可以化称下面这个式子:
c = ∑ ( x i − x ‾ ) ( y i − y ‾ ) ∑ ( x i − x ‾ ) 2 c=\frac{\sum (x_i-\overline x)(y_i-\overline y)}{\sum (x_i-\overline x)^2} c=∑(xi−x)2∑(xi−x)(yi−y)
d = y ‾ − c x ‾ d=\overline y - c\overline x d=y−cx
最小二乘法合理性
这一节是尝试说明最小二乘法的合理性,它同统计理论的许多方法类似。
在贝叶斯线性最小均方估计中,假设估计量和观测向量是线性关系,即: Y ^ = a X + b \hat Y=aX+b Y^=aX+b.求得的线性最小均方估计为:
Θ ^ = c o v ( Y , X ) σ X 2 ( X − μ X ) + μ Y \hat\Theta=\frac{cov(Y,X)}{\sigma _X^2}(X-\mu_X)+\mu_Y Θ^=σX2cov(Y,X)(X−μX)+μY
即 a = c o v ( Y , X ) σ X 2 , b = μ Y − a μ X a=\frac{cov(Y,X)}{\sigma _X^2},b=\mu _Y-a\mu _X a=σX2cov(Y,X),b=μY−aμX
由于不知道 ( X , Y ) (X,Y) (X,Y)的分布,如果用样本均值代替上式中的分布参数:
μ X = x ‾ , μ Y = y ‾ \mu _X=\overline x,\mu _Y=\overline y μX=x,μY=y
c o v ( X , Y ) = E [ ( X − μ X ) ( Y − μ Y ) ] = ∑ [ ( x i − x ‾ ) ( y i − y ‾ ) ] / n cov(X,Y)=E[(X-\mu _X)(Y-\mu _Y)]=\sum [(x_i-\overline x)(y_i-\overline y)]/n cov(X,Y)=E[(X−μX)(Y−μY)]=∑[(xi−x)(yi−y)]/n
σ X 2 = [ ∑ ( x i − x ‾ ) 2 ] / n \sigma_X^2=[\sum(x_i-\overline x)^2]/n σX2=[∑(xi−x)2]/n
则
a = ∑ [ ( x i − x ‾ ) ( y i − y ‾ ) ] ∑ ( x i − x ‾ ) 2 a=\frac {\sum [(x_i-\overline x)(y_i-\overline y)]}{\sum(x_i-\overline x)^2} a=∑(xi−x)2∑[(xi−x)(yi−y)]
可见最小二乘法和线性最小均方估计是类似的。
贝叶斯线性回归
线性回归是一种方法,用线性关系拟合两个量之间的关系,其特点是观测量到拟合直线的距离的平方和最短。所以无论是经典统计推断还是贝叶斯统计推断,凡是要求这种拟合关系的场合,都可以运用线性回归。
多元线性回归
多元线性回归的公式,比一元复杂得多。结合最小二乘法和矩阵的知识,则相对容易求解。常见思路: y = a + a 1 x 1 + a 2 x 2 + a 3 x 3 y=a+a_1x_1+a_2x_2+a_3x_3 y=a+a1x1+a2x2+a3x3,先考虑能否求得 x 2 = h 2 ( x 1 ) , x 3 = h 3 ( x 1 ) x_2=h_2(x_1),x_3=h_3(x_1) x2=h2(x1),x3=h3(x1),这样就能使多远线性规划问题化为一元线=线性回归问题。
非线性回归
非线性回归通常没有闭合式解,对于具体问题需要具体的应对方法。
线性规划注意事项
在解决实际问题问题时,线性回归分析需要考虑以下问题:
- 异方差性。实际问题中观测值的分布的方差可能具有很大的差异性,这样方差很大的观测值对于参数估计将造成不恰当的影响,适当的补救办法是采用加权最小二乘准则。
- 非线性。实际问题并非近似线性关系,用线性回归处理就不合适量。
- 多重共线性。如果有真实关系: y = 2 x + 1 , z = x y=2x+1,z=x y=2x+1,z=x,那么对于 y = a x + b z + c y=ax+bz+c y=ax+bz+c,就无法区分 x , z x,z x,z对 y y y的贡献。
- 过度拟合。用8次多项式拟合8个数据点,显然这是不合适的。经验:数据点的数量应当是待估参数的5~10倍.
- 线性关系不是因果关系,而只是说明相关性。
简单假设检验
假如未知参数 θ \theta θ只有两种取值 { θ 0 , θ 1 } \{\theta_0,\theta_1\} {θ0,θ1},假设检验就是判断接受哪一种假设,分别设为 { H 0 , H 1 } \{H_0,H_1\} {H0,H1}.
现将观测向量 X X X的空间分为两类:1.拒绝域 R R R:若 X ∈ R X\in R X∈R,则认定 H 0 H_0 H0为假,拒绝;2.接受域 R c R^c Rc.
- 第一类错误:错拒.即 H 0 H_0 H0正确而拒绝. α ( R ) = P ( X ∈ R ; H 0 ) \alpha(R)=P(X\in R;H_0) α(R)=P(X∈R;H0)
- 第二类错误:受假. H 0 H_0 H0错误而接受。 β ( R ) = P ( X ∉ R ; H 1 ) \beta(R)=P(X\notin R;H_1) β(R)=P(X∈/R;H1)
- 似然比:两种假设情形下概率的比值():
L ( x ) = p X ( x ; H 1 ) p X ( x ; H 0 ) L(x)=\frac{p_X(x;H_1)}{p_X(x;H_0)} L(x)=pX(x;H0)pX(x;H1)
似然比的临界值需要根据问题来适当选取。
举例子说明。
现在想检验一骰子是否六面均匀,给出两个假设:
H 0 H_0 H0:骰子均匀。 p X ( x ; H 0 ) = 1 / 6 p_X(x;H_0)=1/6 pX(x;H0)=1/6.
H 1 H_1 H1:骰子不均匀。 p X ( x ; H 1 ) = { 1 / 4 , x = 1 , 2 1 / 8 , x = 3 , 4 , 5 , 6 p_X(x;H_1)=\begin{cases} 1/4,x=1,2 \\ 1/8,x=3,4,5,6 \end{cases} pX(x;H1)={1/4,x=1,21/8,x=3,4,5,6
1.先计算似然比函数:
L ( x ) = { 3 / 2 , 当 x = 1 , 2 3 / 4 , 当 x = 3 , 4 , 5 , 6 L(x)=\begin{cases} 3/2, 当x=1,2 \\ 3/4,当x=3,4,5,6 \end{cases} L(x)={3/2,当x=1,23/4,当x=3,4,5,6
2.现在要选取临界值 ξ \xi ξ.临界值会影响拒绝域 R R R。
当 L ( x ) > ξ L(x)>\xi L(x)>ξ时,更倾向于 H 1 H_1 H1,即拒绝 H 0 H_0 H0;
当 L ( x ) < ξ L(x)<\xi L(x)<ξ时,更倾向于 H 0 H_0 H0,即接受 H 0 H_0 H0。
对这个问题似然比 L ( x ) L(x) L(x)只有两个值,如果取 ξ < 3 / 4 \xi<3/4 ξ<3/4,那么 L ( x ) > ξ L(x)>\xi L(x)>ξ总是成立的,即拒绝 H 0 H_0 H0.如果取 ξ > 3 / 2 \xi>3/2 ξ>3/2,那么 L ( x ) < ξ L(x)<\xi L(x)<ξ总是成立的,即接受 H 0 H_0 H0.当 ξ \xi ξ在这两个范围时,拒绝域不依赖于观测值,这是不合适的。所以 ξ \xi ξ选取区间为 [ 3 / 4 , 3 / 2 ] [3/4,3/2] [3/4,3/2].
用错误类型描述上述分析:
第一类错误( H 0 H_0 H0真,而拒绝。即拒绝 H 0 H_0 H0的概率)
α ( ξ ) = { 1 , 当 ξ < 3 / 4 1 3 , 当 3 / 4 < ξ < 3 / 2 0 , 当 ξ > 3 / 2 \alpha(\xi)=\begin{cases}1,当\xi<3/4 \\ \frac{1}{3} , 当3/4<\xi<3/2 \\ 0,当\xi>3/2 \end{cases} α(ξ)=⎩⎪⎨⎪⎧1,当ξ<3/431,当3/4<ξ<3/20,当ξ>3/2
第二类错误( H 0 H_0 H0假,而接受.即接受 H 0 H_0 H0的概率)
β ( ξ ) = { 0 , 当 ξ < 3 / 4 1 / 2 , 当 3 / 4 < ξ < 3 / 2 1 , 当 ξ > 3 / 2 \beta(\xi)=\begin{cases}0,当\xi<3/4 \\ 1/2 , 当3/4<\xi<3/2 \\ 1,当\xi>3/2 \end{cases} β(ξ)=⎩⎪⎨⎪⎧0,当ξ<3/41/2,当3/4<ξ<3/21,当ξ>3/2
这里 ξ \xi ξ的选取,犯第一类错误和犯第二类错误的概率是此消彼长的关系。由于这种平衡存在,没有一种最优的方法选取 ξ \xi ξ.下面是一种常见的方法。
3.选取 ξ \xi ξ
- 确定错误拒绝 H 0 H_0 H0的目标概率 α \alpha α
- 选择 ξ \xi ξ使得 P ( L ( x ) > ξ ; H 0 ) = α P(L(x)>\xi;H_0)=\alpha P(L(x)>ξ;H0)=α.
- 观测 x x x的值,若 L ( x ) > ξ L(x)>\xi L(x)>ξ则拒绝 H 0 H_0 H0
- α \alpha α的典型值是:0.1,0.01,0.05
内曼-皮尔逊引理
内容:现有确定的似然比临界值 ξ \xi ξ(同时确定了拒绝域 R R R),使得犯两类错误的概率分别为:
P ( H 1 ; H 0 ) = P ( L ( x ) > ξ ; H 0 ) = α P(H_1;H_0)=P(L(x)>\xi;H_0)=\alpha P(H1;H0)=P(L(x)>ξ;H0)=α
P ( H 0 ; H 1 ) = P ( L ( x ) < ξ ; H 1 ) = β P(H_0;H_1)=P(L(x)<\xi;H_1)=\beta P(H0;H1)=P(L(x)<ξ;H1)=β
则:
如果有另一个拒绝域使得:
P ( H 1 ; H 0 ) = P ( L ( x ) > ξ ; H 0 ) ≤ α P(H_1;H_0)=P(L(x)>\xi;H_0) \le \alpha P(H1;H0)=P(L(x)>ξ;H0)≤α,则会有 P ( H 0 ; H 1 ) = P ( L ( x ) < ξ ; H 1 ) ≥ β P(H_0;H_1)=P(L(x)<\xi;H_1) \ge \beta P(H0;H1)=P(L(x)<ξ;H1)≥β.
这个引理是说在假设检验中,如果减少犯第一类错误的概率(错误拒绝),那么就会增大犯第二类错误的概率(错误接受).
考虑假设检验的过程,如果 H 0 H_0 H0真假的概率已确定,减少犯第一类错误的概率就是更加倾向于接受 H 0 H_0 H0,所以很自然地,错误接受的概率会相应增大。
显著性检验
当假设检验问题中的可供选择的结果多于2个时,简单假设检验的方法不再适用,“显著性检验”就是为了处理这类问题。“显著性检验”没有确定的解决办法,基本思想是对于一个"假设",找“证据”去“支持/反驳"该假设。
虽然可供选择的结果多余2个,但我们关心的是某一个假设,即原假设 H 0 H_0 H0.我们根据观测向量X,决定接受还是拒绝 H 0 H_0 H0.此时相对于原假设的反面,是备择假设 H 1 H_1 H1:即 H 0 H_0 H0不正确.
举例:投掷一枚硬币n=1000次,每次投掷互相独立, θ \theta θ是硬币朝上的概率,现有原假设 θ = 0.5 \theta=0.5 θ=0.5,备择假设 θ ≠ 0.5 \theta \neq 0.5 θ̸=0.5.
解决流程:
-
选择合适统计量 S S S表达观测数据: S = g ( X 1 , X 2 , . . . , X n ) S=g(X_1,X_2,...,X_n) S=g(X1,X2,...,Xn)
此处 S S S可以选择 S = x 1 + x 2 + . . . + x n , x i ∈ { 0 , 1 } S=x_1+x_2+...+x_n,x_i \in \{0,1\} S=x1+x2+...+xn,xi∈{0,1} -
确定拒绝域 R R R
当 S S S落入拒绝域 R R R时拒绝 H 0 H_0 H0.当然集合 R R R是跟目前未知的临界值 ξ \xi ξ有关的.这里拒绝域可定为: ∣ S − 500 ∣ > ξ |S-500|>\xi ∣S−500∣>ξ -
选择显著性水平:第一类错误的概率 P ( 接 受 H 1 ; H 0 为 真 ) = α P(接受H_1;H_0为真)=\alpha P(接受H1;H0为真)=α
此处选择 α = 0.05 \alpha=0.05 α=0.05 -
选择临界值 ξ \xi ξ
可用正态分布近似二项分布,在 H 0 H_0 H0的条件下(S-500)服从参数为 ( 0 , 250 ) (0,250) (0,250),
P ( ∣ S − 500 ∣ > ξ ; H 0 ) = 0.05 , Φ ( 1.96 ) = 1 − 0.25 = 0.975 P(|S-500|>\xi;H_0)=0.05,\Phi(1.96)=1-0.25=0.975 P(∣S−500∣>ξ;H0)=0.05,Φ(1.96)=1−0.25=0.975
ξ − 0 250 = 1.96 , ξ = 31 \frac{\xi-0}{\sqrt {250}}=1.96,\xi=31 250ξ−0=1.96,ξ=31
如果观测到 S = 472 , ∣ S − 500 ∣ = 28 < ξ S=472,|S-500|=28<\xi S=472,∣S−500∣=28<ξ,则可以说:在5%的显著性水平下不拒绝假设 H 0 H_0 H0.这里5%的意思是该论断犯错误的概率小于5%.“不拒绝”隐含的意思是只倾向于不拒绝,而不是接受。虽然在数学上两者是一个意思。但在这里显然 θ = 0.499999 , 0.499999 , 0.499999999 \theta=0.499999,0.499999,0.499999999 θ=0.499999,0.499999,0.499999999都是可以接受的,不能人为接受其中一个就代表其他的都拒绝。这说明原假设可认为代表一个小的范围,在这个范围里面的取值都是可以的。类似于置信区间的味道。
广义似然比和拟合优度检验
问题:检验给定的分布列是否和观测数据一致,这类问题称为"拟合优度检验"。
给定离散随机变量X的分布列为 P ( X = k ) = q X ( k ) P(X=k)=q_X(k) P(X=k)=qX(k),则可以认为这类问题的原假设为(接受分布列):
H 0 : p X = ( q X ( 1 ) , q X ( 2 ) , . . . , q X ( n ) ) H_0:p_X=(q_X(1),q_X(2),...,q_X(n)) H0:pX=(qX(1),qX(2),...,qX(n))
H 1 : P ≠ ( q X ( 1 ) , q X ( 2 ) , . . . , q X ( n ) ) H_1:P \neq (q_X(1),q_X(2),...,q_X(n)) H1:P̸=(qX(1),qX(2),...,qX(n))
现在为了对 H 0 H_0 H0进行判断,采用"广义似然比"的方法。“广义似然比”就是假设 H 1 H_1 H1为最大似然估计:
H 1 : P = ( θ ^ 1 , θ ^ 2 , . . . , θ ^ n ) H_1:P=(\hat\theta_1,\hat\theta_2,...,\hat\theta_n) H1:P=(θ^1,θ^2,...,θ^n),其中 θ ^ i \hat\theta_i θ^i是 p X ( k ) p_X(k) pX(k)的最大似然估计.
这里用 q X ( k ) q_X(k) qX(k)表示这是一条假设的分布列,用以区分X的真实分布列 p X ( k ) p_X(k) pX(k).
广义似然比为:
P ( X = x 1 , x 2 , . . . , x n ; q ) P ( X = x 1 , x 2 , . . . , x n ; θ ^ ) \frac{P(X=x_1,x_2,...,x_n;q)}{P(X=x_1,x_2,...,x_n;\hat\theta)} P(X=x1,x2,...,xn;θ^)P(X=x1,x2,...,xn;q)
通常采用对数的方法,可以简化计算。