斯坦福大学公开课-傅里叶变换及其应用-学习记录1-傅里叶级数

本文是对斯坦福大学公开课-傅里叶变换及其应用的一些学习总结
对应的课程视频链接为：课程链接
课程用到的讲义下载地址：讲义链接

傅里叶变换这一名词已经在很多地方都有见过了，之前也是对其有一些粗略的了解，那么现在想跟着这个课程与讲义稍微深入一点地学习，在这里记录一下个人的总结与感悟。

第一篇对应课程的第1-5节，讲义的第一章，即傅里叶级数。傅里叶级数在高数中已经学过了，但是当时只是以应付考试的心理马马虎虎地看了一下，对它的理解肯定是不到位的。

周期性

傅里叶级数是指可以将一个周期函数表示成正弦函数和余弦函数的无穷级数，它研究的对象就是具有周期性的函数，那么首先来复习一下周期性的相关内容。
周期性的定义：如果存在 T>0 T > 0 满足 f(t+T)=f(t) f ( t + T ) = f ( t ) ，那么就说 f f 具有周期性，其周期为 T T 。很显然如果 T T 是 f f 的一个周期，那么 2T、3T、4T……nT 2 T 、 3 T 、 4 T … … n T 都是 f f 的周期，一般提到的周期都是所有这些周期中最小的那个，即最小正周期。
周期函数的和：考虑函数 f(t)=cos2πt+12cos4πt f ( t ) = c o s 2 π t + 1 2 c o s 4 π t ，它是两个周期分别为 1、12 1 、 1 2 的函数的和，那么 f(t) f ( t ) 的周期是多少？这种问题高中的时候应该经常见过，很显然它的周期应该是 1 1 ，在这个例子中，周期函数的和也是一个周期函数。现在进行一般性的考虑，对于任意的两个周期函数，它们的和也是周期函数吗？考虑函数 f(t)=cost+cos2–√t f ( t ) = c o s t + c o s 2 t ，它是两个周期分别为 2π、2–√π 2 π 、 2 π 的函数之和，但是很遗憾，这个函数并不是一个周期函数，是没有办法找到一个 T T 满足 f(t+T)=f(t) f ( t + T ) = f ( t ) 的，它的图像如下图所示。

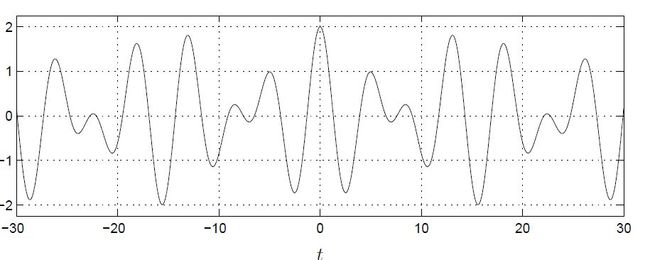
事实上，如果两个周期函数之和是一个周期函数，那么它们的周期必须满足其中一个周期是另一个周期的整数倍的关系。
在经过了数个世纪的关于周期现象的研究后，对于周期问题，前人在数学层面提出了三个重要的观点：
1.刻画最简单的周期现象的函数是sin、cos，但是不管是在理论还是实际地运算中，都采用复指数的形式来代替独立的三角函数，即欧拉公式： eix=cosx+isinx e i x = c o s x + i s i n x
2.研究的函数的平方积分，应该是有界的，即： ∫ba|f(t)|2dt<∞ ∫ a b | f ( t ) | 2 d t < ∞
3.Eigenfunction of a linear operator D,especially differential operators。
（不知道该如何翻译= =），查了一下wiki，这句话的意思是， D D 是定义在一个函数空间中的一个线性运算，对于在任意的该空间下的非零函数 f f ，都有 Df=λf D f = λ f ，其中 λ λ 是一个标量，被称作特征值。这句话中提到的“尤其是微分运算”可以表述为如下等式：
df(t)dt=λf(t) d f ( t ) d t = λ f ( t )

可能现在还是一头雾水，不知道这三条的意义是什么，不过不用担心，先接着往下看。

累加形式

由简单的周期函数，将其累加可以构造复杂的周期函数，傅里叶当时就是猜测任意一个周期函数都可以用如下的形式来表达：

∑n=1NAnsin(2πnt+ϕn) ∑ n = 1 N A n s i n ( 2 π n t + ϕ n )

这样的形式可以很好地表现相位、频率等信息，但是计算起来并不方便，更常用的形式为：

∑n=1N(ancos(2πnt)+bnsin(2πnt)) ∑ n = 1 N ( a n c o s ( 2 π n t ) + b n s i n ( 2 π n t ) )

推导：

∑n=1NAnsin(2πnt+ϕn)=∑n=1NAnsin2πntcosϕn+Ancos2πntsinϕn ∑ n = 1 N A n s i n ( 2 π n t + ϕ n ) = ∑ n = 1 N A n s i n 2 π n t c o s ϕ n + A n c o s 2 π n t s i n ϕ n

令 Ancosϕn=an,Ansinϕn=bn A n c o s ϕ n = a n , A n s i n ϕ n = b n 即可。

如果再加上 n=0 n = 0 的情况就可以得到：

a02+∑n=1N(ancos(2πnt)+bnsin(2πnt)) a 0 2 + ∑ n = 1 N ( a n c o s ( 2 π n t ) + b n s i n ( 2 π n t ) )

注意这里用的是 a02 a 0 2 ，为什么不写 a0 a 0 呢？
前面提到了，应该采用复指数的形式来代替孤立的sin、cos，那么现在将上式转成对应的复指数形式：

∑n=−NNcne2πint ∑ n = − N N c n e 2 π i n t

这里会有一些疑惑，为什么求和范围变成了-N到N，并且求和式是不是过于简单了？现在将这个式子的复指数展开成三角函数来看一看：

∑n=−NNcne2πint=∑n=−NNcn(cos2πnt+isin2πnt) ∑ n = − N N c n e 2 π i n t = ∑ n = − N N c n ( c o s 2 π n t + i s i n 2 π n t )

这里sin的前边有i，但是实际上之前所表达的和式的sin前边是不带i的，这就提醒我们，这里的 cn c n 是复数，不是实数。如果我们将 cn c n 写成 cn=an+ibn c n = a n + i b n ，那么就可以写出：

∑n=−NNcn(cos2πnt+isin2πnt)=∑n=−NN(an+ibn)(cos2πnt+isin2πnt) ∑ n = − N N c n ( c o s 2 π n t + i s i n 2 π n t ) = ∑ n = − N N ( a n + i b n ) ( c o s 2 π n t + i s i n 2 π n t )

=∑n=−NNancos2πnt+anisin2πnt+ibncos2πnt−bnsin2πnt = ∑ n = − N N a n c o s 2 π n t + a n i s i n 2 π n t + i b n c o s 2 π n t − b n s i n 2 π n t

现在假如这个求和范围是0到N，那么最终的结果一定是带i的，因为中间的 anisin2πnt+ibncos2πnt a n i s i n 2 π n t + i b n c o s 2 π n t 没办法消掉。可是如果求和范围改成-N到N呢？考虑当n=k和n=-k时的情形：

n=k时：akcos2πkt+akisin2πkt+ibkcos2πkt−bksin2πkt n = k 时 ： a k c o s 2 π k t + a k i s i n 2 π k t + i b k c o s 2 π k t − b k s i n 2 π k t

n=−k时：a−kcos2πkt−a−kisin2πkt+ib−kcos2πkt+b−ksin2πkt n = − k 时 ： a − k c o s 2 π k t − a − k i s i n 2 π k t + i b − k c o s 2 π k t + b − k s i n 2 π k t

如果说我们令 a−k=ak a − k = a k ， b−k=−bk b − k = − b k ，那么上面这两个式子的和就是：

2akcos2πkt−0+0−2bksin2πkt 2 a k c o s 2 π k t − 0 + 0 − 2 b k s i n 2 π k t

，是没有i的形式，因此求和范围设为-N到N是很有用的一种消除i的手段，由此我们可以知道， cn c n 是一个复数，并且满足 c−n=cn¯¯¯¯¯ c − n = c n ¯ ， cn¯¯¯¯¯ c n ¯ 是 cn c n 的共轭。并且可以得出c_n与原式中的a_n、b_n的关系：

cn=an2−ibn2 c n = a n 2 − i b n 2

因此当n=0时， c0=a02−ib02=a02 c 0 = a 0 2 − i b 0 2 = a 0 2 ，这也就是为什么在之前要将常数项写成 a02 a 0 2 的原因！因为这样更加简便。

系数C的求解

现在我们猜测一个周期函数可以被表达为： ∑Nn=−Ncne2πint ∑ n = − N N c n e 2 π i n t 的形式，（牢记： cn c n 是复数，且 c−n=cn¯¯¯¯¯ c − n = c n ¯ ），那么到底可不可以实现这一目标呢？其实就是能不能求出这样的一系列系数 cn c n 呢？现在假设

f(t)=∑n=−NNcne2πint f ( t ) = ∑ n = − N N c n e 2 π i n t

，现在如果要求 ck c k ，考虑将 ck c k 分离出来：

−cke2πikt=−f(t)+∑n=−Nk−1cne2πint+∑n=k+1Ncne2πint − c k e 2 π i k t = − f ( t ) + ∑ n = − N k − 1 c n e 2 π i n t + ∑ n = k + 1 N c n e 2 π i n t

再两边同乘 e−2πikt e − 2 π i k t ，就得到：

−ck=−f(t)e−2πikt+∑n=−Nk−1cne2πi(n−k)t+∑n=k+1Ncne2πi(n−k)t − c k = − f ( t ) e − 2 π i k t + ∑ n = − N k − 1 c n e 2 π i ( n − k ) t + ∑ n = k + 1 N c n e 2 π i ( n − k ) t

好像没有办法再处理了？这里就体现了数学的美妙之处，如果说两侧都对t在0到1上积分呢？逐项考虑：

∫10−ckdt=−ck ∫ 0 1 − c k d t = − c k

∫10cne2πi(n−k)tdt={0,cn, n ≠ k  n = k ∫ 0 1 c n e 2 π i ( n − k ) t d t = { 0 ,  n ≠ k  c n ,  n = k

很显然，右侧的每一个 n n 都满足 n≠k n ≠ k ，因此我们最终得到了 ck c k 的表达式：

ck=∫10f(t)e−2πiktdt c k = ∫ 0 1 f ( t ) e − 2 π i k t d t

对应的

c−k=∫10f(t)e−2πiktdt¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯=∫10f(t)¯¯¯¯¯¯¯¯e−2πikt¯¯¯¯¯¯¯¯¯¯¯¯¯dt=∫10f(t)e2πiktdt c − k = ∫ 0 1 f ( t ) e − 2 π i k t d t ¯ = ∫ 0 1 f ( t ) ¯ e − 2 π i k t ¯ d t = ∫ 0 1 f ( t ) e 2 π i k t d t

注意 f(t) f ( t ) 是实数，其共轭等于自身。
注意到

c0=∫10f(t)dt c 0 = ∫ 0 1 f ( t ) d t

即 f(t) f ( t ) 在区间[0,1]上的平均值。
经过求解 cn c n ，就可以将

∑n=−NNcne2πint ∑ n = − N N c n e 2 π i n t

称作傅里叶级数。

一般周期的傅里叶级数

注意到上述傅里叶级数所表达的函数，都是周期为1的函数。但是并不是所有的周期函数的周期都为1，当一个周期函数的周期为 T(T≠1) T ( T ≠ 1 ) 时，该如何写出它的傅里叶级数？
设 f(t) f ( t ) 的周期为 T(T≠1) T ( T ≠ 1 ) ，那么设 g(t)=f(Tt) g ( t ) = f ( T t ) ，显然 g(t) g ( t ) 的周期为1。那么 g(t) g ( t ) 就可以由上述傅里叶级数表达：

g(t)=∑n=−NNcne2πint=f(Tt) g ( t ) = ∑ n = − N N c n e 2 π i n t = f ( T t )

设 Tt=s T t = s ，则

f(s)=∑n=−NNcne2πinsT f ( s ) = ∑ n = − N N c n e 2 π i n s T

因此

f(t)=∑n=−NNcne2πintT f ( t ) = ∑ n = − N N c n e 2 π i n t T

那么傅里叶系数呢？

cn=∫10e−2πintg(t)dt=∫T0e−2πinsTf(s)dsT=1T∫T0e−2πinsTf(s)ds c n = ∫ 0 1 e − 2 π i n t g ( t ) d t = ∫ 0 T e − 2 π i n s T f ( s ) d s T = 1 T ∫ 0 T e − 2 π i n s T f ( s ) d s

因此

cn=1T∫T0e−2πinsTf(t)dt c n = 1 T ∫ 0 T e − 2 π i n s T f ( t ) d t

，由周期性也可以写成：

cn=1T∫T/2−T/2e−2πintTf(t)dt c n = 1 T ∫ − T / 2 T / 2 e − 2 π i n t T f ( t ) d t

将函数看成向量的扩展

对于傅里叶级数，其实可以从另一个角度来看，我们考虑把函数看成无限维的向量，函数的自变量看成向量的某一维，在[0,1]区间内自变量的取值是无限的，函数的值看成向量在某一维上的取值，类比向量的运算，来定义函数的一些运算。
函数的内积： f(t)⋅g(t)=(f(t),g(t))=∫10f(t)g(t)dt f ( t ) · g ( t ) = ( f ( t ) , g ( t ) ) = ∫ 0 1 f ( t ) g ( t ) d t ，对于含复数的函数定义其内积为： (f(t),g(t))=∫10f(t)g(t)¯¯¯¯¯¯¯¯dt ( f ( t ) , g ( t ) ) = ∫ 0 1 f ( t ) g ( t ) ¯ d t
函数的正交性： 当(f(t),g(t))=0 当 ( f ( t ) , g ( t ) ) = 0 时，称两函数是正交的
函数的二范数： ||f||=(f,f)=∫10f(t)⋅f(t)¯¯¯¯¯¯¯¯dt=∫10|f(t)|2−−−−−−−−−−−−−−−−−−−−−−−−−−−√ | | f | | = ( f , f ) = ∫ 0 1 f ( t ) · f ( t ) ¯ d t = ∫ 0 1 | f ( t ) | 2

很显然对于两个复指数作内积，会有：

(en,em)=∫10e2πinte2πimt¯¯¯¯¯¯¯¯¯¯¯¯=∫10e2πinte−2πimt=∫10e2πi(n−m)t={0,1, n ≠ m  n = m ( e n , e m ) = ∫ 0 1 e 2 π i n t e 2 π i m t ¯ = ∫ 0 1 e 2 π i n t e − 2 π i m t = ∫ 0 1 e 2 π i ( n − m ) t = { 0 ,  n ≠ m  1 ,  n = m

即当 n≠m n ≠ m 时， en,em e n , e m 是正交的。

有了如上基础，现在来重新看一下傅里叶级数的这个式子：

∑n=−NNcne2πint ∑ n = − N N c n e 2 π i n t

cn=∫10f(t)e−2πintdt c n = ∫ 0 1 f ( t ) e − 2 π i n t d t

发现了什么？ cn c n 是两个函数的内积！ cn=∫10f(t)e2πint¯¯¯¯¯¯¯¯¯¯¯dt c n = ∫ 0 1 f ( t ) e 2 π i n t ¯ d t ，即 cn=(f(t),e2πint) c n = ( f ( t ) , e 2 π i n t ) ，而这个 e2πint e 2 π i n t 正好是傅里叶级数中的那一项，这意味着什么？
回想一下在线性空间中，表示一个向量在某个线性空间下的坐标是如何表示的？ p=α1v1+α2v2+α3v3+……+αnvn p = α 1 v 1 + α 2 v 2 + α 3 v 3 + … … + α n v n ，其中 (v1,v2,v3,……,vn) ( v 1 , v 2 , v 3 , … … , v n ) 是线性空间下的一组基，那么这个向量的坐标就是 (α1,α2,α3,……,αn) ( α 1 , α 2 , α 3 , … … , α n ) ，当这组基中的所有向量都是正交的时候， α α 的值应等于向量到每个基向量上的投影，即 αn=(p,v1) α n = ( p , v 1 ) 。
回到傅里叶级数中，设集合 V=[e2πint,n∈[−N,N]] V = [ e 2 π i n t , n ∈ [ − N , N ] ] ，这个集合中的所有函数都是正交的，因为n的取值都是不同的！所以我们可以把集合V看做是在某个线性空间下的一组基，而傅里叶系数 cn c n 正好就是 f(t) f ( t ) 在这个函数空间下的坐标！即 cn c n 相当于 f(t) f ( t ) 投影到每个基函数上的投影长度，傅里叶级数实质上就是将原函数在由某个正交的基函数组构成的线性空间下分解到每一维上的结果！
从这个角度来看，傅里叶级数就不是偶然的、灵光一现得到的，而是一个合理的、可以解释其由来的结果！

帕萨瓦尔定理

信号的能量由 ∫10|f(t)|2dt ∫ 0 1 | f ( t ) | 2 d t 表示，帕萨瓦尔定理指出，信号的能量等于其经过傅里叶变换后在频域上的面积积分，即

∫10|f(t)|2dt=∑n=−∞∞|cn|2 ∫ 0 1 | f ( t ) | 2 d t = ∑ n = − ∞ ∞ | c n | 2

证明：

∫10|f(t)|2dt=||f||2=(f,f)=(∑n=−∞∞(f,en)en,∑m=−∞∞(f,em)em)=∑n,m(f,en)(f,em)¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(en,em)=∑n=−∞∞(f,en)f,en¯¯¯¯¯¯¯¯¯¯=∑n=−∞∞|(f,en)|2=∑n=−∞∞|cn|2 ∫ 0 1 | f ( t ) | 2 d t = | | f | | 2 = ( f , f ) = ( ∑ n = − ∞ ∞ ( f , e n ) e n , ∑ m = − ∞ ∞ ( f , e m ) e m ) = ∑ n , m ( f , e n ) ( f , e m ) ¯ ( e n , e m ) = ∑ n = − ∞ ∞ ( f , e n ) f , e n ¯ = ∑ n = − ∞ ∞ | ( f , e n ) | 2 = ∑ n = − ∞ ∞ | c n | 2

最佳L^2三角逼近

一个度数为N、有限的傅里叶级数是平方可积函数空间下的最佳三角逼近，该定理的公式化描述为：

||f−∑n=−NN(f,en)en||≤||f−∑n=−NNαnen|| | | f − ∑ n = − N N ( f , e n ) e n | | ≤ | | f − ∑ n = − N N α n e n | |

，当且仅当对任意的n都有 αn=(f,en) α n = ( f , e n ) 时取等。
证明：

||f−∑−NNαnen||2=||f−∑n=−NN(f,en)en+∑n=−NN(f,en)en−∑n=−NNαnen||2= | | f − ∑ − N N α n e n | | 2 = | | f − ∑ n = − N N ( f , e n ) e n + ∑ n = − N N ( f , e n ) e n − ∑ n = − N N α n e n | | 2 =

||(f−∑n=−NN(f,en)en)+(∑n=−NN(f,en)en−∑n=−NNαnen)||2= | | ( f − ∑ n = − N N ( f , e n ) e n ) + ( ∑ n = − N N ( f , e n ) e n − ∑ n = − N N α n e n ) | | 2 =

||f−∑n=−NN(f,en)en||2+2(f−∑n=−NN(f,en)en,∑m=−NN((f,em)−αm)em)+ | | f − ∑ n = − N N ( f , e n ) e n | | 2 + 2 ( f − ∑ n = − N N ( f , e n ) e n , ∑ m = − N N ( ( f , e m ) − α m ) e m ) +

||∑n=−NN((f,en)−αn)en)||2 | | ∑ n = − N N ( ( f , e n ) − α n ) e n ) | | 2

注意到中间的这一项：

2(f−∑n=−NN(f,en)en,∑m=−NN((f,em)−αm)em) 2 ( f − ∑ n = − N N ( f , e n ) e n , ∑ m = − N N ( ( f , e m ) − α m ) e m )

其中 ((f,em)−αm) ( ( f , e m ) − α m ) 是一个标量，因此这一项实际上可以看做是一系列的
(f−∑Nn=−N(f,en)en,em) ( f − ∑ n = − N N ( f , e n ) e n , e m ) 乘上一个标量再累加的结果，
而 (f−∑Nn=−N(f,en)en,em)=(f,em)−∑Nn=−N(f,en)(en,em)=(f,em)−(f,em)=0 ( f − ∑ n = − N N ( f , e n ) e n , e m ) = ( f , e m ) − ∑ n = − N N ( f , e n ) ( e n , e m ) = ( f , e m ) − ( f , e m ) = 0 ，因此中间一项为0！
而最后一项

||∑n=−NN((f,en)−αn)en)||2 | | ∑ n = − N N ( ( f , e n ) − α n ) e n ) | | 2

由帕萨瓦尔定理可知，它等于

∑n=−NN|(f,en)−αn|2 ∑ n = − N N | ( f , e n ) − α n | 2

，因此将变换后的这两项带入到原式中可得：

||f−∑−NNαnen||2=||f−∑n=−NN(f,en)en||2+∑n=−NN|(f,en)−αn|2 | | f − ∑ − N N α n e n | | 2 = | | f − ∑ n = − N N ( f , e n ) e n | | 2 + ∑ n = − N N | ( f , e n ) − α n | 2

显然这足够证明：

||f−∑−NNαnen||≥||f−∑n=−NN(f,en)en|| | | f − ∑ − N N α n e n | | ≥ | | f − ∑ n = − N N ( f , e n ) e n | |

实际应用-热方程求解

现在考虑一个圆环，用 u(x,t) u ( x , t ) 表示圆环在 x x 位置处在经过时间 t t 后的温度，现在如果给定了 t=0 t = 0 时的 u(x,0) u ( x , 0 ) ，并且有一个物理关系： ut=12uxx u t = 1 2 u x x 如何求解 u(x,t) u ( x , t ) 的表达式？
显然 u(x,t) u ( x , t ) 对 x x 具有周期性，那么我们可以先对 x x 做傅里叶变换：

u(x,t)=∑−∞∞cn(t)e2πinx u ( x , t ) = ∑ − ∞ ∞ c n ( t ) e 2 π i n x

cn(t)=∫10u(x,t)e−2πinxdx c n ( t ) = ∫ 0 1 u ( x , t ) e − 2 π i n x d x

对傅里叶系数求导得： c′n(t)=∫10ut(x,t)e−2πinxdx=∫1012uxx(x,t)e−2πinxdx c n ′ ( t ) = ∫ 0 1 u t ( x , t ) e − 2 π i n x d x = ∫ 0 1 1 2 u x x ( x , t ) e − 2 π i n x d x
这个积分式利用两次分布积分可以进一步转换：
∫1012uxx(x,t)e−2πinxdx=∫1012e−2πinxdux(x,t)=12(e−2πinxux(x,t)|10−∫10(−2πin)e−2πinxux(x,t)dx)=12(e−2πinxux(x,t)|10−∫10(−2πin)e−2πinxdu(x,t)) ∫ 0 1 1 2 u x x ( x , t ) e − 2 π i n x d x = ∫ 0 1 1 2 e − 2 π i n x d u x ( x , t ) = 1 2 ( e − 2 π i n x u x ( x , t ) | 0 1 − ∫ 0 1 ( − 2 π i n ) e − 2 π i n x u x ( x , t ) d x ) = 1 2 ( e − 2 π i n x u x ( x , t ) | 0 1 − ∫ 0 1 ( − 2 π i n ) e − 2 π i n x d u ( x , t ) )
而 ∫10(−2πin)e−2πinxdu(x,t)=((−2πin)e−2πinxu(x,t))|10+∫10(4π2n2)e−2πinxu(x,t)dx ∫ 0 1 ( − 2 π i n ) e − 2 π i n x d u ( x , t ) = ( ( − 2 π i n ) e − 2 π i n x u ( x , t ) ) | 0 1 + ∫ 0 1 ( 4 π 2 n 2 ) e − 2 π i n x u ( x , t ) d x
注意到： (e−2πinxux(x,t))|10=ux(1,t)−ux(0,t)=0 ( e − 2 π i n x u x ( x , t ) ) | 0 1 = u x ( 1 , t ) − u x ( 0 , t ) = 0 (周期性)
((−2πin)e−2πinxu(x,t))|10=u(1,t)−u(0,t)=0 ( ( − 2 π i n ) e − 2 π i n x u ( x , t ) ) | 0 1 = u ( 1 , t ) − u ( 0 , t ) = 0 (周期性)，代入可得：
c′n(t)=−2π2n2∫10e−2πinxu(x,t)dx=−2π2n2cn(t) c n ′ ( t ) = − 2 π 2 n 2 ∫ 0 1 e − 2 π i n x u ( x , t ) d x = − 2 π 2 n 2 c n ( t )
这是一个非常简单的常微分方程，可以解得： cn(t)=cn(0)e−2π2n2t c n ( t ) = c n ( 0 ) e − 2 π 2 n 2 t ， cn(0) c n ( 0 ) 是t=0时的傅里叶系数，可以由给定的初始温度算出来，那么最后得到的 u(x,t) u ( x , t ) 表达式为

u(x,t)=∑n=−∞∞cn(0)e−2π2n2te2πinx u ( x , t ) = ∑ n = − ∞ ∞ c n ( 0 ) e − 2 π 2 n 2 t e 2 π i n x

更多的内容

讲义中还有一些关于傅里叶级数收敛的讨论，时间有限，并且我自己也不是数学系的，也就没必要继续深入阅读了，有兴趣的可以自行阅读讲义的相关内容。