深度学习笔试知识点及面试常考题

深度学习发展史：

  忽略前面那些铺垫，直接介绍深度学习爆发期的历史

 

  1. 2012 AlexNet

  成功利用relu 代替 sigmoid函数，解决了sigmoid函数的梯度弥散问题

  添加了drop out 层，防止过拟合

  采用最大池化，代替平均池化

 

 2. 2014 VGG

  通过反复堆叠3*3 小型卷积核和2*2 的最大池化层

 

3. 2014 inception net

采用1*1的卷积，选取稀疏结构即多个分支。

而 inception v2 提出了著名的Batch Normalization,并且将大的卷积核变为多个小的卷积核

 

4. 2015 Resnet

提出了残差学习单元bottleneck 或者 skip connection，有两种单元，一种是两个3*3，一种是两个1*1核一个3*3

通过残差直连的方式来解决网络退化的问题，或者过梯度消失或者梯度爆炸的过程。

 

 

 

5. RNN 、LSTM 和 GRU

相比rnn,lstm模型利用三个门来解决梯度消失和爆炸，分别是输入门、忘记门和输出门；gru 将输入与忘记门合二为一，本质上没有区别，但是参数较少，训练速度快。

6.FCN 、UNet

 

知识点汇总：

1. Feature Map的尺寸等于(input_size + 2 * padding_size − filter_size)/stride+1
2. bn为什么能加快收敛速度。bn解决了什么问题？bn是怎么计算的？基于什么计算的？训练和测试的时候有什么不同？测试时候的均值和方差是怎么来的？

BN理解：

N的基本思想其实相当直观：因为深层神经网络在做非线性变换前的激活输入值（就是那个x=WU+B，U是输入）随着网络深度加深或者在训练过程中，其分布逐渐发生偏移或者变动，之所以训练收敛慢，一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近（对于Sigmoid函数来说，意味着激活输入值WU+B是大的负值或正值），所以这导致反向传播时低层神经网络的梯度消失，这是训练深层神经网络收敛越来越慢的本质原因，而BN就是通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布，其实就是把越来越偏的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，意思是这样让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。

　　THAT’S IT。其实一句话就是：对于每个隐层神经元，把逐渐向非线性函数映射后向取值区间极限饱和区靠拢的输入分布强制拉回到均值为0方差为1的比较标准的正态分布，使得非线性变换函数的输入值落入对输入比较敏感的区域，以此避免梯度消失问题。因为梯度一直都能保持比较大的状态，所以很明显对神经网络的参数调整效率比较高，就是变动大，就是说向损失函数最优值迈动的步子大，也就是说收敛地快。BN说到底就是这么个机制，方法很简单，道理很深刻

参考文章（https://www.cnblogs.com/guoyaohua/p/8724433.html）

注意BN训练和测试的不同

训练时，基于每一个batch进行归一化

测试时，根据训练时所有的数据，即所有batch的期望，计算参数

 

3. 池化层的作用？池化层反向传播的时候是怎么计算的？

池化层主要有以下几个作用: 
a 降维 
b 实现非线性 
c 可以扩大感知野 
d 可以实现不变性:平移不变性,旋转不变性,尺度不变性

 

反向传播计算方法：

Pooling池化操作的反向梯度传播

CNN网络中另外一个不可导的环节就是Pooling池化操作，因为Pooling操作使得feature map的尺寸变化，假如做2×2的池化，假设那么第l+1层的feature map有16个梯度，那么第l层就会有64个梯度，这使得梯度无法对位的进行传播下去。其实解决这个问题的思想也很简单，就是把1个像素的梯度传递给4个像素，但是需要保证传递的loss（或者梯度）总和不变。根据这条原则，mean pooling和max pooling的反向传播也是不同的。

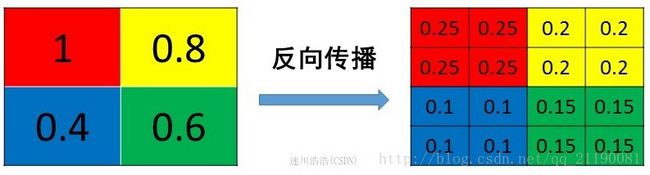
1）、mean pooling

mean pooling的前向传播就是把一个patch中的值求取平均来做pooling，那么反向传播的过程也就是把某个元素的梯度等分为n份分配给前一层，这样就保证池化前后的梯度（残差）之和保持不变，还是比较理解的，图示如下 ：

mean pooling比较容易让人理解错的地方就是会简单的认为直接把梯度复制N遍之后直接反向传播回去，但是这样会造成loss之和变为原来的N倍，网络是会产生梯度爆炸的。

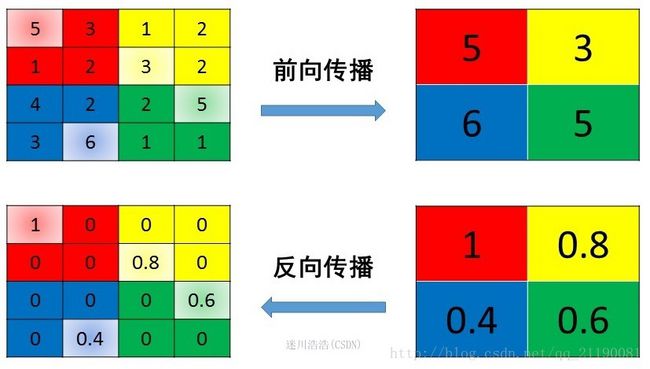
2）、max pooling

max pooling也要满足梯度之和不变的原则，max pooling的前向传播是把patch中最大的值传递给后一层，而其他像素的值直接被舍弃掉。那么反向传播也就是把梯度直接传给前一层某一个像素，而其他像素不接受梯度，也就是为0。所以max pooling操作和mean pooling操作不同点在于需要记录下池化操作时到底哪个像素的值是最大，也就是max id，这个变量就是记录最大值所在位置的，因为在反向传播中要用到，那么假设前向传播和反向传播的过程就如下图所示 ：

4. 激活函数优缺点比较

1）.Sogmoid函数 (Logistic 函数) 
公式：f(z)=11+e−zf(z)=11+e−z 
将实数映射到(0,1),可用来二分类

缺点: 激活函数计算量大 
反向传播时，容易出现梯度消失的情况

2）.Tanh函数 (双曲正切函数) 
公式：f(z)=tanh(z)=ez−e−zez+e−zf(z)=tanh(z)=ez−e−zez+e−z 
将实数映射到[-1,1] 
双曲正切函数在特征明显的时候效果会更好。

3）.ReLu函数 
公式：ϕ(x)=max(0,x)ϕ(x)=max(0,x) 
优点：收敛速度快 
缺点：训练时候很“脆弱”，很容易“die”