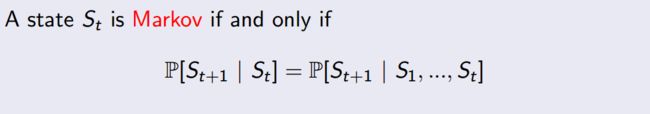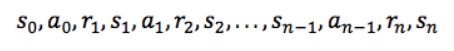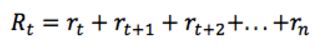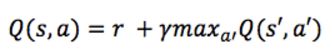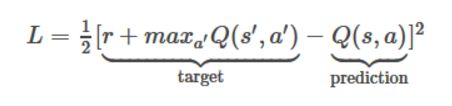Reinforcement Learning 的核心基础概念及实现
2013 年伦敦的一家小公司 DeepMind 发表了一篇论文 Playing Atari with Deep Reinforcement Learning 。论文描述了如何教会电脑玩 Atari 2600 游戏(仅仅让电脑观察游戏的每一帧图像和接受游戏分数的上升作为奖励信号)。结果很令人满意,因为电脑比大多数人类玩家玩的好,而且该模型在没有任何改变的情况下,学会了玩其他游戏,并且在三个游戏中表现比人类玩家好!自此通用人工智能的话题开始火热 -- 能够适应各种负责环境而不仅仅局限于玩棋类游戏,而 DeepMind 因此被谷歌看中而被收购。2015 年,DeepMind 又发表了一篇 Human-level control through deep reinforcement learning,在本篇论文中 DeepMind 用同样的模型,教会电脑玩49种游戏,而且过半游戏比专业玩家玩得更好。2016年3月,AlphaGo 与围棋世界冠军、职业九段选手李世石进行人机大战,并以4:1的总比分获胜;2016年末2017年初,该程序在中国棋类网站上以“大师”(Master)为注册帐号与中日韩数十位围棋高手进行快棋对决,连续60局无一败绩。
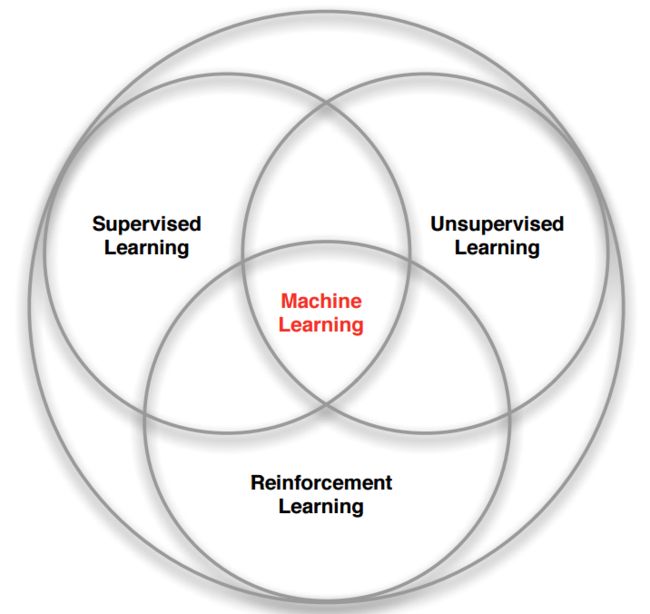
自此,在机器学习领域,除了监督学习和非监督学习,强化学习(Reinforcement Learning)也逐渐走进人们的视野。
强化学习
以打砖块游戏为例,游戏中你控制底部的挡板来反弹小球,来清除屏幕上半部分的砖块。每次你打中砖块,分数增加,你也得到一个奖励,而没有接到小球则会受到惩罚。
假设让一个神经网络来玩这个游戏, 输入是屏幕图像,输出将是三个动作:左,右或发射球。很明显这是一个分类问题,对于每一帧图像,我们计算到到一个动作即可(为屏幕数据分类)。 但是听起来很简单,实际上有很多有挑战性的细节。因为我们当前的动作奖励有可能是在此之后一段时间获得的。不像监督学习,对于每一个样本,都有一个确定的标签与之对应,而强化学习没有标签,只有一个时间延迟的奖励,而且游戏中我们往往牺牲当前的奖励来获取将来更大的奖励。因为我们的小球在打到砖块,获得奖励时,事实上挡板并没有移动,该奖励是由于之前的一系列动作来获得的。这就是信用分配问题(Credit Assignment Problem),即当前的动作要为将来获得更多的奖励负责。
而且在我们找到一个策略,让游戏获得不错的奖励时,我们是选择继续坚持当前的策略,还是探索新的策略以求更多的奖励?这就是探索与开发(Explore-exploit Dilemma)的问题。
强化学习就是一个重要的解决此类问题的模型,它是从我们的人类经验中总结出来的。在现实生活中,如果我们做某件事获得奖励,那么我们会更加偏向于做这件事。比如你的狗狗早上给你把鞋子叼过来,你对他说 Good dog 并奖励它,那么狗狗会更加偏向于叼鞋。而且人类每天在学校的成绩、在家来自父母的夸奖、还是工作上的薪水本质上都是在奖励。
马尔可夫决策过程 (Markov Decision Process)
那么如何用数学的方法来解决此类问题呢?最常用的方法就是那此类问题看作一个马尔可夫决策过程 (Markov Decision Process)。
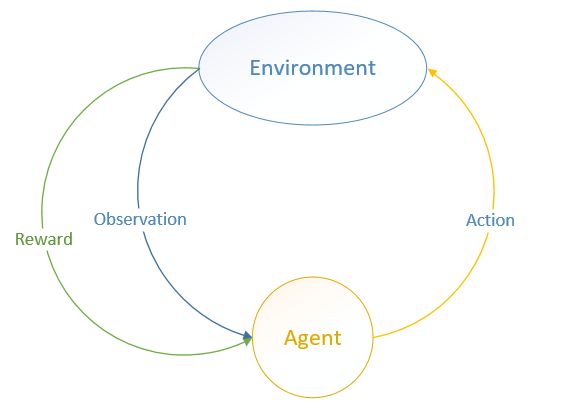
MDP 中有两个对象:Agent 和 Environment。
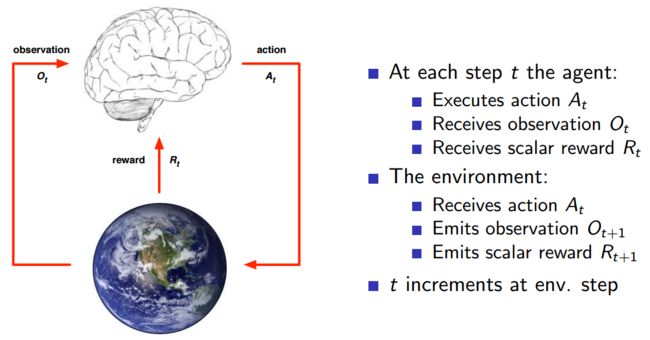
Environment 处于一个特定的状态(State)(如打砖块游戏中挡板的位置、各个砖块的状态等),Agent 可以通过执行特定的动作( Actions )(如向左向右移动挡板)来改变 Environment 的状态, Environment 状态改变之后会返回一个观察(Observation)给Agent,同时还会得到一个奖励(Reward)(可以为负,就是惩罚),这样 Agent 根据返回的信息采取新的动作,如此反复下去。Agent 如何选择动作叫做策略(Policy)。MDP 的任务就是找到一个策略,来最大化奖励。
具体的执行步骤如上图图所示。注意 State 和 Observation 区别:State 是 Environment 的私有表达,我们往往不知道不会直接到的。在 MDP 中,当前状态State (Markov state)包含了所有历史信息,即将来只和现在有关,与过去无关,因为现在状态包含了所有历史信息。举个例子,在一个遵循牛顿第二定律的世界里,我们随意抛出一个小球,某一时刻 t 知道了小球的速度和加速度,那么 t 之后的小球的位置都可以由当前状态,根据牛顿第二定律计算出来。再举一个夸张的例子,如果宇宙大爆炸时奇点的状态已知,那么以后的所有状态就已经确定,包括人类进化、我写这篇文章和你在阅读这篇文章都是可以根据那一状态推断出来的。当然这只是理想状况,现实往往不会那么简单(因为这只是马尔科夫的一个假设)。只有满足这样条件的状态才叫做马尔科夫状态。即:
正是因为 State 太过于复杂,我们往往可以需要一个对 Environment 的观察来间接获得信息,因此就有了 Observation。不过 Observation 是可以等于 State 的,在游戏中,一帧游戏画面完全可以代表当前状态,因此 Observation = State,此时叫做 Full Observability。
状态、动作、状态转移概率组成了 MDP,一个 MDP 周期(episode )由一个有限的状态、动作、奖励队列组成:
这里 si 代表状态,ai 代表行动,ri + 1(下标 i+1)是执行动作后的奖励。 最终状态为sn(例如“游戏结束”)。
折扣未来奖励(Discounted Future Reward)
为了获得更多的奖励,我们往往不能只看当前奖励,更要看将来的奖励。
给定一个 MDP 周期,总的奖励显然为:
那么,从当前时间 t 开始,总的将来的奖励为:
但是 Environment 往往是随机的,执行特定的动作不一定得到特定的状态,因此将来的奖励所占的权重要依次递减,因此使用 discounted future reward 代替:
这里 γ 是0和1之间的折扣因子 —— 越是未来的奖励,折扣越多,权重越小。而明显上式是个迭代过程,因此可以写作:
即当前时刻的奖励等于当前时刻的即时奖励加上下一时刻的奖励乘上折扣因子 γ。如果 γ 等于0,意味着只看当前奖励;如果 γ 等于1,意味着环境是确定的,相同的动作总会获得相同的奖励。因此实际中 γ 往往取类似0.9这样的值。因此我们的任务变成了找到一个策略,最大化将来的奖励 R。
Q-learning
在 Q-learning 中,我们定义一个函数 Q(s,a),表示在状态 s 执行动作 a 时的最大折扣未来奖励,并从此刻开始优化它:
把 Q(s,a) 看作是在状态 s,执行动作 a时,游戏结束时的分数就行了。不要惊奇为什么在状态 s 就可以知道游戏结束时的分数,因为这是马尔科夫过程,将来只和现在有关,现在是将来的充分条件。这样最大化 Q(s,a) 就相当于最大化我们游戏的得分了(至于为什么叫做 Q,因为它代表了在特定状态 s 下特定动作 a 的质量"quality")。
假设你处于状态 s,思考应该采取行动 a 或 b 以在比赛结束时获得最高分的动作。一旦有了 Q函数,答案就变得一目了然 —— 选择 Q 值最高的动作:
这里的 π 代表策略,代表我们如何在某状态选取动作。
怎么才能得到这个Q函数呢? 只关注一个转换
这就是贝尔曼方程(Bellman equation),当前状态 s 的最大将来奖励等于下一状态 s' 的最大将来奖励乘以折扣因子。这样我们就可以用贝尔曼方程来近似了,最简单的方法就是把Q函数看作二维数组,行代表状态,列代表动作,那么算法描述如下:
α是一个学习速率(learning rate),它控制了先前的Q值和新的Q值之间的差异有多少被考虑在内。 特别地,当α = 1时,则两个 Q [s,a] 抵消,更新与贝尔曼方程完全相同。
我们用来更新 Q [s,a] 的 maxQ [s',a'] 一开始只是随机的,但随着迭代,会慢慢收敛,最终近似于真实值。具体的例子可以参看这里:A Painless Q-Learning Tutorial (中文版:一个 Q-learning 算法的简明教程),详细地一步一步介绍了是怎么收敛的。
Deep Q Network
打砖块游戏中的环境状态可以由挡板的位置,球的位置和方向以及每个砖块的存在或不存在来定义。然而,这种直观的表示只能代表具体的游戏。有通用的方法适合所有的游戏吗?答案是屏幕像素 —— 它们隐含地包含关于游戏情况的所有相关信息,球的速度和方向也可以包含在连续两个屏幕像素中。
如果我们使用 DeepMind 论文中的预处理方法,将游戏画面放缩为 84×84,并将其转换为256灰度级的灰度级,我们将拥有 25684x84x4≈10的67970次方 个可能的游戏状态。这意味着Q表中有10的67970次方 行 —— 超过已知宇宙中的原子数!即使某些像素组合永远不会发生 —— 我们可以将其表示为仅包含访问状态的稀疏矩阵,但是,状态还是很多,而且难以收敛。
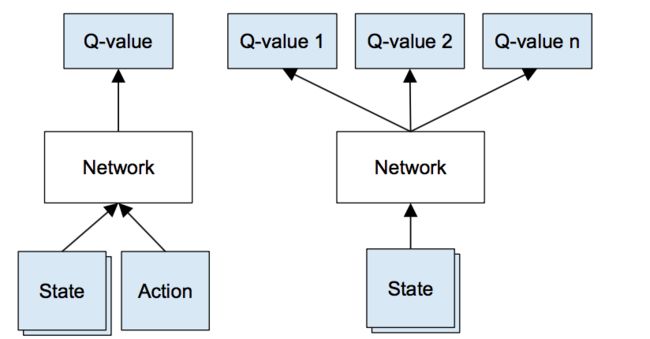
这时候深度学习登场了,神经网络可以高效的表示高维数据,将其映射为低维数据。 因此我们可以用神经网络代表我们的Q函数,将状态(游戏画面)和动作作为输入,并输出相应的Q值。 或者,我们只能将游戏画面作为输入,并输出每个可能动作的Q值。 这种方法的优点是,如果我们要执行Q值更新或选择具有最高Q值的动作,我们只需要通过网络进行一次前进传播,并且可以立即获得所有动作的Q值 。
输入是四个 84×84 灰度级游戏画面,输出是每个可能动作的Q值(在Atari中为18)。 Q值可以是任何实际值,这使得它成为一个回归任务,可以用简单的平方误差损失进行优化:
给定转换
- 对当前状态 s 进行前向传播以获取所有动作的Q值。
- 对下一个状态 s' 进行前向传播,并计算最大Q值 max Q(s’, a’)。
- 将动作对应的目标Q值设置为 r + γ max Q(s',a')(步骤2中计算的最大值)。
- 使用反向传播算法更新参数。
经验回放 (Experience Replay)
现在我们使用卷积神经网络近似Q函数。但事实证明,使用非线性函数近似Q值不是非常稳定,而且难以收敛,在单GPU上需要很长时间,差不多一个星期才会看到成效。
有很多技巧可以优化,最重要的技巧是经验回放。在游戏过程中,所有的经历
探索与开发(Exploration-Exploitation)
首先,当Q表或Q网络被随机初始化时,其预测最初也是随机的。如果我们选择具有最高Q值的动作,则该动作也将是随机的,这时 Agent 执行的动作是随机的。随着Q函数的收敛,返回更一致的Q值,探索量将减少,此时这些一致的Q值叫做开发(Exploitation)。但是这些探索是“贪心”的,它发现第一个有效策略后停止收敛,很有可能我们只是找到了一个局部最优解。
对于上述问题,一个简单而有效的解决方案是 ε-greedy exploration —— 以概率 ε 选择一个随机动作,否则选择具有最高Q值“贪婪”动作。DeepMind 实际上将 ε 随时间从1减少到0.1,一 开始,系统完全随机移动,最大限度地探索状态空间,然后稳定的利用开发率。
最终带有经验回放的算法如下:
DeepMind 还有更多的技巧来优化,如目标网络,错误剪辑,奖励剪辑等,但这些都不在此介绍范围之内。
实现
下面使用 TensorFlow 实现 Q 算法,解决 OpenAI Gym 的 CartPole 游戏和 FlappyBird 游戏。
Q 算法的 Q函数我么可以用任何函数来代替,不限于神经网络或者卷积神经网络,因此我们需要把它抽象出来:
class Model():
def __init__(self, num_outputs):
self.num_outputs = num_outputs
def definition(self):
raise NotImplementedError
def get_num_outputs(self):
return self.num_outputsModel 代表了Q函数的抽象,num_outputs 代表了可能的动作个数,CartPole 中有两个:左移或者右移;FlappyBird 也有两个动作:点击屏幕或者什么都不做。definition 函数代表具体的Q函数定义,返回输入和输出。
因为游戏是不确定的,所以我们需要抽象一个 Env :
# Env-related abstractions
class Env():
def step(self, action_index):
raise NotImplementedError
def reset(self):
raise NotImplementedError
def render(self):
raise NotImplementedErrorEnv 可以是任何游戏,或者其他问题。step 函数表示执行指定动作 action_index,然后返回一个元组:(state, reward, terminal, info),state 是游戏当前状态,如屏幕像素;reward 是奖励,可以为负数; terminal 代表游戏是否结束;info 代表一些其他信息,可有可无。
然后是我们的算法实现:
import numpy as np
import tensorflow as tf
import random
import numpy as np
import time
import sys
import collections
class DeepQNetwork():
def __init__(self,
model,
env,
optimizer=tf.train.AdamOptimizer,
learning_rate=0.001,
gamma=0.9,
replay_memeory_size=10000,
batch_size=32,
initial_epsilon=0.5,
final_epsilon=0.01,
decay_factor=1,
logdir=None,
save_per_step=1000,
test_per_epoch=100):
self.model = model
self.env = env
self.num_actions = model.get_num_outputs()
self.learning_rate = learning_rate
self.optimizer = optimizer
self.gamma = gamma
self.epsilon = initial_epsilon
self.initial_epsilon = initial_epsilon
self.final_epsilon = final_epsilon
self.decay_factor = decay_factor
self.logdir = logdir
self.test_per_epoch = test_per_epoch
self.replay_memeory = collections.deque()
self.replay_memeory_size = replay_memeory_size
self.batch_size = batch_size
self.define_q_network()
# session
self.sess = tf.InteractiveSession()
self.sess.run(tf.global_variables_initializer())
if self.logdir is not None:
if not self.logdir.endswith('/'): self.logdir += '/'
self.save_per_step = save_per_step
self.saver = tf.train.Saver()
checkpoint_state = tf.train.get_checkpoint_state(self.logdir)
if checkpoint_state and checkpoint_state.model_checkpoint_path:
path = checkpoint_state.model_checkpoint_path
self.saver.restore(self.sess, path)
print('Restore from {} successfully.'.format(path))
else:
print('No checkpoint.')
self.summaries = tf.summary.merge_all()
self.summary_writer = tf.summary.FileWriter(
self.logdir, self.sess.graph)
sys.stdout.flush()
def define_q_network(self):
self.input_states, self.q_values = self.model.definition()
self.input_actions = tf.placeholder(tf.float32,
[None, self.num_actions])
# placeholder of target q values
self.input_q_values = tf.placeholder(tf.float32, [None])
# only use selected q values
action_q_values = tf.reduce_sum(
tf.multiply(self.q_values, self.input_actions),
reduction_indices=1)
self.global_step = tf.Variable(0, trainable=False)
# define cost
self.cost = tf.reduce_mean(
tf.square(self.input_q_values - action_q_values))
self.optimizer = self.optimizer(self.learning_rate).minimize(
self.cost, global_step=self.global_step)
tf.summary.scalar('cost', self.cost)
tf.summary.scalar('reward', tf.reduce_mean(action_q_values))
def egreedy_action(self, state):
if random.random() <= self.epsilon:
action_index = random.randint(0, self.num_actions - 1)
else:
action_index = self.action(state)
if self.epsilon > self.final_epsilon:
self.epsilon *= self.decay_factor
return action_index
def action(self, state):
q_values = self.q_values.eval(feed_dict={self.input_states:
[state]})[0]
return np.argmax(q_values)
def do_train(self, epoch):
# randomly select a batch
mini_batches = random.sample(self.replay_memeory, self.batch_size)
state_batch = [batch[0] for batch in mini_batches]
action_batch = [batch[1] for batch in mini_batches]
reward_batch = [batch[2] for batch in mini_batches]
next_state_batch = [batch[3] for batch in mini_batches]
# target q values
target_q_values = self.q_values.eval(
feed_dict={self.input_states: next_state_batch})
input_q_values = []
for i in range(len(mini_batches)):
terminal = mini_batches[i][4]
if terminal:
input_q_values.append(reward_batch[i])
else:
# Discounted Future Reward
input_q_values.append(reward_batch[i] +
self.gamma * np.max(target_q_values[i]))
feed_dict = {
self.input_actions: action_batch,
self.input_states: state_batch,
self.input_q_values: input_q_values
}
self.optimizer.run(feed_dict=feed_dict)
step = self.global_step.eval()
if self.saver is not None and epoch > 0 and step % self.save_per_step == 0:
summary = self.sess.run(self.summaries, feed_dict=feed_dict)
self.summary_writer.add_summary(summary, step)
self.summary_writer.flush()
self.saver.save(self.sess, self.logdir + 'dqn', self.global_step)
# num_epoches: train epoches
def train(self, num_epoches):
for epoch in range(num_epoches):
epoch_rewards = 0
state = self.env.reset()
# 9999999999: max step per epoch
for step in range(9999999999):
# ε-greedy exploration
action_index = self.egreedy_action(state)
next_state, reward, terminal, info = self.env.step(
action_index)
# one-hot action
one_hot_action = np.zeros([self.num_actions])
one_hot_action[action_index] = 1
# store trans in replay_memeory
self.replay_memeory.append((state, one_hot_action, reward,
next_state, terminal))
# remove element if exceeds max size
if len(self.replay_memeory) > self.replay_memeory_size:
self.replay_memeory.popleft()
# now train the model
if len(self.replay_memeory) > self.batch_size:
self.do_train(epoch)
# state change to next state
state = next_state
epoch_rewards += reward
if terminal:
# Game over. One epoch ended.
break
# print("Epoch {} reward: {}, epsilon: {}".format(
# epoch, epoch_rewards, self.epsilon))
# sys.stdout.flush()
#evaluate model
if epoch > 0 and epoch % self.test_per_epoch == 0:
self.test(epoch, max_step_per_test=99999999)
def test(self, epoch, num_testes=10, max_step_per_test=300):
total_rewards = 0
print('Testing...')
sys.stdout.flush()
for _ in range(num_testes):
state = self.env.reset()
for step in range(max_step_per_test):
# self.env.render()
action = self.action(state)
state, reward, terminal, info = self.env.step(action)
total_rewards += reward
if terminal:
break
average_reward = total_rewards / num_testes
print("epoch {:5} average_reward: {}".format(epoch, average_reward))
sys.stdout.flush()解释一下这个算法:__init__ 方法除了 env 和 model 是必须的,其他都是可选的。
optimizer指定了 Tensorflow 使用的优化器;learning_rate是学习速率;gamma就是算法中的折扣因子 γ;replay_memeory_size是存放经验的最大数量;batch_size是从经验池取经验用于训练的大小;epsilon就是 ε-greedy exploration 中的 ε,表示epsilon将从initial_epsilon以decay_factor的速率下降到final_epsilon为止,decay_factor等于1表示不下降;logdir是 Tensorflow 保存模型的路径,为None表示不保存训练结果;save_per_step是每多少步保存一下断点;test_per_epoch是每多少不测试评估一下训练进度。
定义q network 的损失函数:
def define_q_network(self):
self.input_states, self.q_values = self.model.definition()
self.input_actions = tf.placeholder(tf.float32,
[None, self.num_actions])
# placeholder of target q values
self.input_q_values = tf.placeholder(tf.float32, [None])
# only use selected q values
action_q_values = tf.reduce_sum(
tf.multiply(self.q_values, self.input_actions),
reduction_indices=1)
self.global_step = tf.Variable(0, trainable=False)
# define cost
self.cost = tf.reduce_mean(
tf.square(self.input_q_values - action_q_values))
self.optimizer = self.optimizer(self.learning_rate).minimize(
self.cost, global_step=self.global_step)
tf.summary.scalar('cost', self.cost)
tf.summary.scalar('reward', tf.reduce_mean(action_q_values))然后是 train 方法:
# num_epoches: train epoches
def train(self, num_epoches):
for epoch in range(num_epoches):
epoch_rewards = 0
state = self.env.reset()
# 9999999999: max step per epoch
for step in range(9999999999):
# ε-greedy exploration
action_index = self.egreedy_action(state)
next_state, reward, terminal, info = self.env.step(
action_index)
# one-hot action
one_hot_action = np.zeros([self.num_actions])
one_hot_action[action_index] = 1
# store trans in replay_memeory
self.replay_memeory.append((state, one_hot_action, reward,
next_state, terminal))
# remove element if exceeds max size
if len(self.replay_memeory) > self.replay_memeory_size:
self.replay_memeory.popleft()
# now train the model
if len(self.replay_memeory) > self.batch_size:
self.do_train(epoch)
# state change to next state
state = next_state
epoch_rewards += reward
if terminal:
# Game over. One epoch ended.
break
# print("Epoch {} reward: {}, epsilon: {}".format(
# epoch, epoch_rewards, self.epsilon))
# sys.stdout.flush()
#evaluate model
if epoch > 0 and epoch % self.test_per_epoch == 0:
self.test(epoch, max_step_per_test=99999999)这里我们把 (state, one_hot_action, reward, next_state, terminal) 元组存在队列中,如果队列长度大于 batch_size 就开始训练。
然后是具体的训练:
def do_train(self, epoch):
# randomly select a batch
mini_batches = random.sample(self.replay_memeory, self.batch_size)
state_batch = [batch[0] for batch in mini_batches]
action_batch = [batch[1] for batch in mini_batches]
reward_batch = [batch[2] for batch in mini_batches]
next_state_batch = [batch[3] for batch in mini_batches]
# target q values
target_q_values = self.q_values.eval(
feed_dict={self.input_states: next_state_batch})
input_q_values = []
for i in range(len(mini_batches)):
terminal = mini_batches[i][4]
if terminal:
input_q_values.append(reward_batch[i])
else:
# Discounted Future Reward
input_q_values.append(reward_batch[i] +
self.gamma * np.max(target_q_values[i]))
feed_dict = {
self.input_actions: action_batch,
self.input_states: state_batch,
self.input_q_values: input_q_values
}
self.optimizer.run(feed_dict=feed_dict)
step = self.global_step.eval()
if self.saver is not None and epoch > 0 and step % self.save_per_step == 0:
summary = self.sess.run(self.summaries, feed_dict=feed_dict)
self.summary_writer.add_summary(summary, step)
self.summary_writer.flush()
self.saver.save(self.sess, self.logdir + 'dqn', self.global_step)首先随机选择一批数据,然后计算 Target Q 值,最后训练即可。
接下来用真实的游戏测试一下吧!
CartPole
CartPole 比较简单,状态只是一个一个4维的实数值向量,像这样:
[-0.00042486 -0.02710707 0.01032103 -0.04882064]我们完全不用管这四个实数具体什么意思,管它是什么角度、加速度等,让神经网络自己理解去吧!
定义我们的 CartPoleEnv,使用 Open AI 的 Gym:
class CartPoleEnv(Env):
def __init__(self):
self.env = gym.make('CartPole-v0')
def step(self, action_index):
s, r, t, i = self.env.step(action_index)
return s, r, t, i
def reset(self):
return self.env.reset()
def render(self):
self.env.render()定义 Q 函数,一个简单的神经网络(4-16-2,4代表输入,16代表隐层神经元个数,2代表两个动作对应的Q值),因为 CartPole 太简单了:
model = SimpleNeuralNetwork([4, 16, 2])然后开始训练:
model = SimpleNeuralNetwork([4, 16, 2])
env = CartPoleEnv()
qnetwork = DeepQNetwork(
model=model, env=env, learning_rate=0.0001, logdir='./tmp/CartPole/')
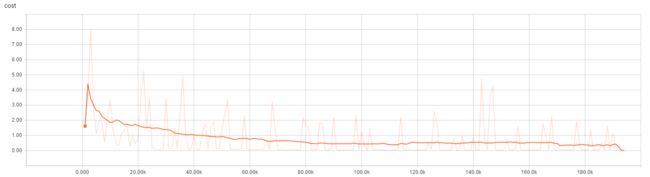
qnetwork.train(4000)一开始完全是随机的,但随着迭代次数增加,效果越来越好(可以直接运行查看效果),而且收敛的非常快,80.0k 之后几乎完全收敛:
FlappyBird
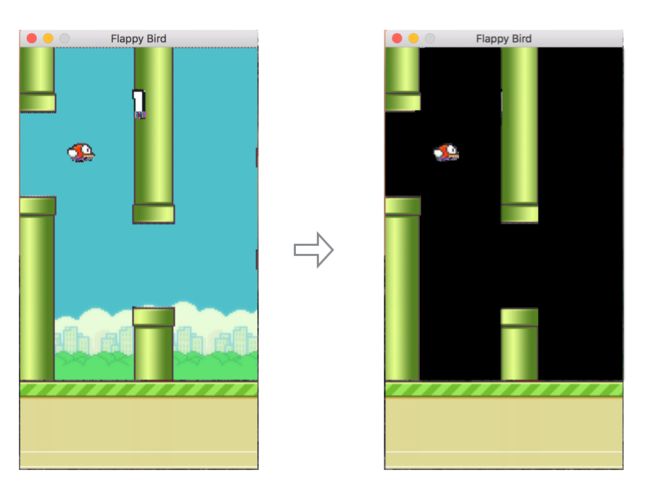
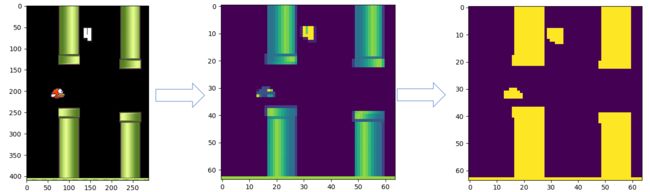
FlappyBird 比较复杂,我们采用原始屏幕像素作为输入。但是为了加快收敛,使用了一下技巧:
抽取游戏背景:
裁剪掉下部无用数据:
放缩为64x64并二值化:
然后就可以使用神经网络训练了:
model = CNN(img_w=image_size, img_h=image_size, num_outputs=2)
env = FlappyBirdEnv()
qnetwork = DeepQNetwork(
model=model,
env=env,
learning_rate=1e-8,
initial_epsilon=0.1,
final_epsilon=0,
decay_factor=0.99,
save_per_step=1000,
logdir='./tmp/FlappyBird/')
if train:
qnetwork.train(10000)
else:
runGame(env, network)为了加快收敛,我使用了这样一个技巧:
因为 FlappyBird 大部分时间是什么都不做的,只有在很少概率情况下才会点击屏幕,所以,在探索阶段,让它更所的几率(95%)选择什么都不做。(你不用修改也没关系,但会增加训练时间)
def egreedy_action(self, state):
#Exploration
if random.random() <= self.epsilon:
if random.random() < 0.95:
action_index = 0
else:
action_index = 1
# action_index = random.randint(0, self.num_actions - 1)
else:
#Exploitation
action_index = self.action(state)
if self.epsilon > self.final_epsilon:
self.epsilon *= self.decay_factor
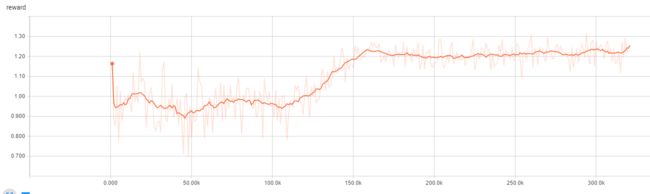
return action_index而且训练过程中,我也动态了调整了 learning rate,让它更快的收敛。经过这些优化,很快就进行了收敛(两个小时,使用CPU训练,而不用等上一整天):
最后来个Gif:
最后源码在这里。
参考
- Guest Post (Part I): Demystifying Deep Reinforcement Learning
- UCL Course on RL
- A Painless Q-Learning Tutorial
- DQN 从入门到放弃1 DQN与增强学习
-- END