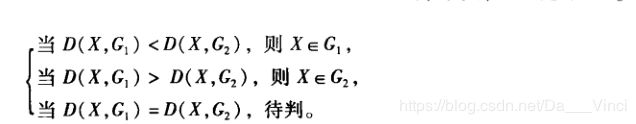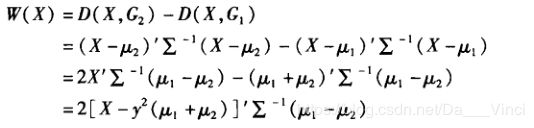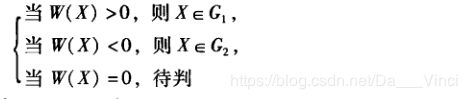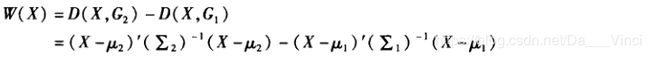判别分析及R实现

目录

简介

两总体距离判别

R实现

 马氏距离判别

 线性判别分析

 多总体距离判别

Bayes判别准则

什么是先验概率

先验概率取相等

先验概率取不相等

判别分析小结

---

简介

根据已知分类数据，分别计算各类重心，即是各组的均值，距离判别准则是，对任给的一次观测，若他与第i类的重心最近，就认为他来自第i类

两总体距离判别

设有两个总体 G1和G2，从第一个总体中抽取n1个样品，从第二个总体中抽取n2个样品，对每个样品测量p个指标，取任一个样品实测指标为X=（x1，x3，xp）‘，分别计算样品X到总体G1和G2的距离D（X,G1）和D（X，G2），按距离最近准测判别分类，即是

具体而言，设μ1，μ2、∑1、∑2、分别为总体G1和G2的均值向量和协方差阵，通常采用马氏距离进行判别，即：

（1）当∑1=∑2=∑时，设

令

则

为线性判别函数

其中

于是可根据W（X）的正负性判定所取样本的类别：

（2）当∑1！=∑2时，仍然用

为判别函数，不过它是X的二次函数，而不是上面那中情况下的线性函数

R实现

> d = read.table("clipboard",header=T)
> attach(d)
> d
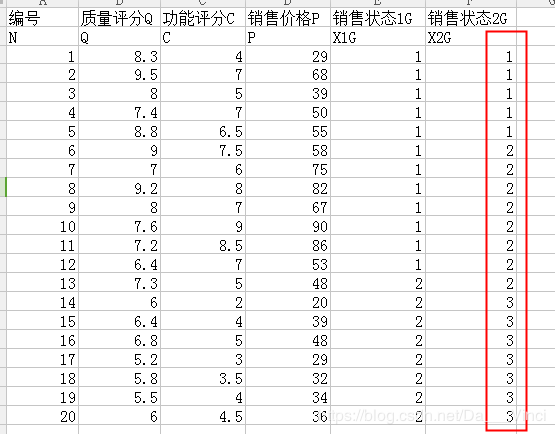
    N   Q   C  P X1G X2G
1   1 8.3 4.0 29   1   1
2   2 9.5 7.0 68   1   1
3   3 8.0 5.0 39   1   1
4   4 7.4 7.0 50   1   1
5   5 8.8 6.5 55   1   1
6   6 9.0 7.5 58   1   2
7   7 7.0 6.0 75   1   2
8   8 9.2 8.0 82   1   2
9   9 8.0 7.0 67   1   2
10 10 7.6 9.0 90   1   2
11 11 7.2 8.5 86   1   2
12 12 6.4 7.0 53   1   2
13 13 7.3 5.0 48   2   2
14 14 6.0 2.0 20   2   3
15 15 6.4 4.0 39   2   3
16 16 6.8 5.0 48   2   3
17 17 5.2 3.0 29   2   3
18 18 5.8 3.5 32   2   3
19 19 5.5 4.0 34   2   3
20 20 6.0 4.5 36   2   3

 

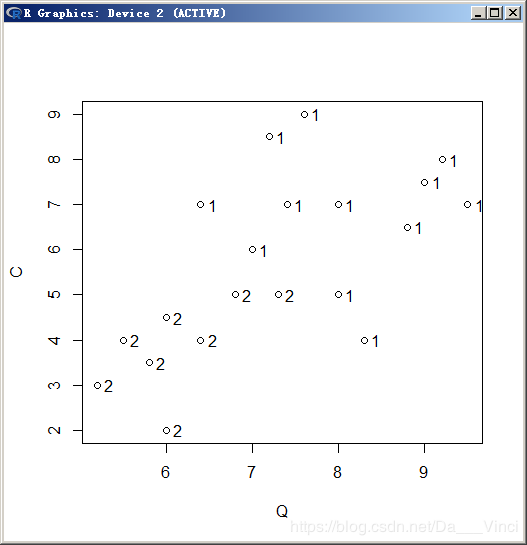
> plot(Q,C);text(Q,C,X1G,adj = -0.8)
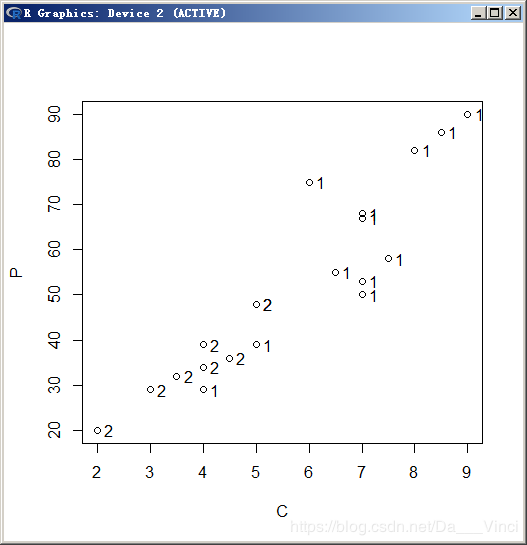
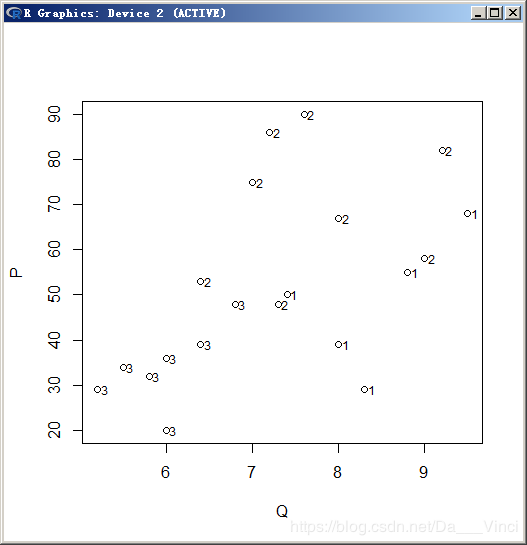
> plot(Q,P);text(Q,P,X1G,adj = -0.8)
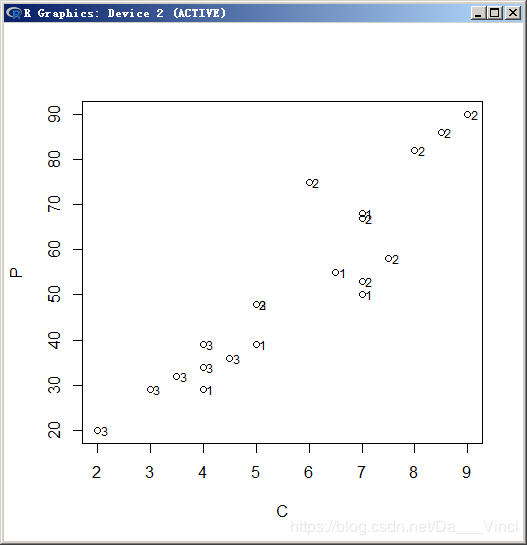
> plot(C,P);text(C,P,X1G,adj = -0.8)

 质量评分分类图

功能评分分类图

销售价格分类图

 马氏距离判别

X1G是组别，其他三项是数据

> library(MASS) #
> qd=qda(X1G~Q+C+P);qd
Call:
qda(X1G ~ Q + C + P)

Prior probabilities of groups:
  1   2 
0.6 0.4 

Group means:
         Q     C        P
1 8.033333 6.875 62.66667
2 6.125000 3.875 35.75000
>

 预测组别与原始组别完全一致

> cbind(X1G,newG=predict(qd)$class)
      X1G newG
 [1,]   1    1
 [2,]   1    1
 [3,]   1    1
 [4,]   1    1
 [5,]   1    1
 [6,]   1    1
 [7,]   1    1
 [8,]   1    1
 [9,]   1    1
[10,]   1    1
[11,]   1    1
[12,]   1    1
[13,]   2    2
[14,]   2    2
[15,]   2    2
[16,]   2    2
[17,]   2    2
[18,]   2    2
[19,]   2    2
[20,]   2    2
>

 预测新数据的组别，属于第一类

> predict(qd,data.frame(Q=8,C=7.5,P=65))
$`class`
[1] 1
Levels: 1 2

$posterior
          1           2
1 0.9968009 0.003199091

> 

 线性判别分析

在协方差矩阵相等的情况下，可以使用线性判别

> ld=lda(X1G~Q+C+P);ld
Call:
lda(X1G ~ Q + C + P)

Prior probabilities of groups:
  1   2 
0.6 0.4 

Group means:
         Q     C        P
1 8.033333 6.875 62.66667
2 6.125000 3.875 35.75000

Coefficients of linear discriminants:
          LD1
Q -0.71588142
C -0.80733209
P  0.02519526
> 

> W=predict(ld)
> cbind(X1G,Wx=W$x,newG=W$class)
   X1G        LD1 newG
1    1  0.0379520    1
2    1 -2.2604870    1
3    1 -0.3026631    1
4    1 -1.2106506    1
5    1 -1.6832423    1
6    1 -2.5581649    1
7    1  0.5129155    2
8    1 -2.5003210    1
9    1 -1.2118601    1
10   1 -1.9606808    1
11   1 -1.3714432    1
12   1 -0.4191834    1
13   2  0.4252112    1
14   2  3.0723861    2
15   2  1.6500793    2
16   2  0.7831519    2
17   2  3.0645165    2
18   2  2.3069074    2
19   2  2.1683963    2
20   2  1.4571800    2
> 

 结果显示有两个样品数据判断错误，说明我们的协方差矩阵相等的假设有待商议。

> predict(ld,data.frame(Q=8,C=7.5,P=65)) #判定
$`class`
[1] 1
Levels: 1 2
$posterior
         1           2
1 0.998577 0.001422957
$x
        LD1
1 -1.665917
> 

 多总体距离判别

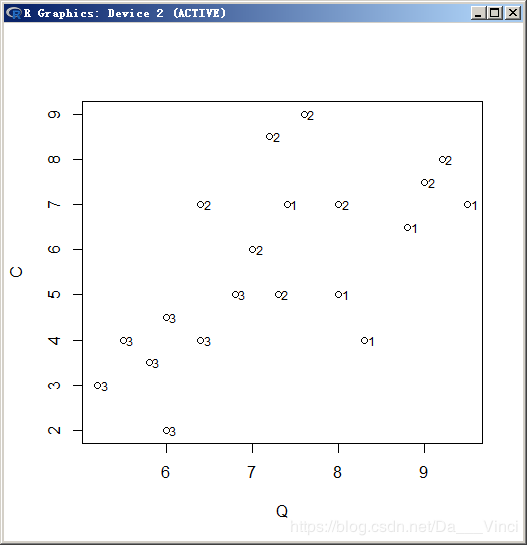
plot(Q,C);text(Q,C,X2G,adj=-0.5,cex=0.75)
plot(Q,P);text(Q,P,X2G,adj=-0.5,cex=0.75)        
plot(C,P);text(C,P,X2G,adj=-0.5,cex=0.75) 

 

等方差

> ld=lda(X2G~Q+C+P); ld
Call:
lda(X2G ~ Q + C + P)

Prior probabilities of groups:
   1    2    3 
0.25 0.40 0.35 

Group means:
     Q    C    P
1 8.40 5.90 48.2
2 7.71 7.25 69.9
3 5.96 3.71 34.0

Coefficients of linear discriminants:
      LD1     LD2
Q -0.8117  0.8841
C -0.6309  0.2013
P  0.0158 -0.0878

Proportion of trace:
 LD1  LD2 
0.74 0.26 
> Z=predict(ld)
> newG=Z$class
> cbind(X2G,round(Z$x,3),newG)
   X2G    LD1    LD2 newG
1    1 -0.141  2.583    1
2    1 -2.392  0.825    1
3    1 -0.370  1.642    1
4    1 -0.971  0.548    1
5    1 -1.713  1.247    1
6    2 -2.459  1.362    1
7    2  0.379 -2.200    2
8    2 -2.558 -0.467    2
9    2 -1.190 -0.413    2
10   2 -1.764 -2.382    2
11   2 -1.187 -2.486    2
12   2 -0.112 -0.599    2
13   2  0.340  0.233    3
14   3  2.846  0.937    3
15   3  1.559  0.026    3
16   3  0.746 -0.209    3
17   3  3.006 -0.359    3
18   3  2.251  0.009    3
19   3  2.211 -0.331    3
20   3  1.521  0.036    3
> (tab=table(X2G,newG))
   newG
X2G 1 2 3
  1 5 0 0
  2 1 6 1
  3 0 0 7
> diag(prop.table(tab,1))
   1    2    3 
1.00 0.75 1.00 
> sum(diag(prop.table(tab)))
[1] 0.9
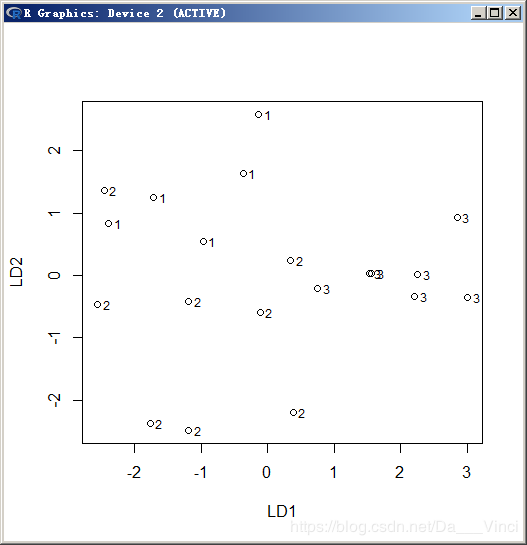
> plot(Z$x)
> text(Z$x[,1],Z$x[,2],X2G,adj=-0.8,cex=0.75)
> predict(ld,data.frame(Q=8,C=7.5,P=65)) #判定
$`class`
[1] 2
Levels: 1 2 3

$posterior
      1     2       3
1 0.211 0.787 0.00178

$x
    LD1    LD2
1 -1.54 -0.137

不等方差

> qd=qda(X2G~Q+C+P); qd
Call:
qda(X2G ~ Q + C + P)

Prior probabilities of groups:
   1    2    3 
0.25 0.40 0.35 

Group means:
     Q    C    P
1 8.40 5.90 48.2
2 7.71 7.25 69.9
3 5.96 3.71 34.0
> Z=predict(qd)
> newG=Z$class
> cbind(X2G,newG)
      X2G newG
 [1,]   1    1
 [2,]   1    1
 [3,]   1    1
 [4,]   1    1
 [5,]   1    1
 [6,]   2    2
 [7,]   2    2
 [8,]   2    2
 [9,]   2    2
[10,]   2    2
[11,]   2    2
[12,]   2    2
[13,]   2    3
[14,]   3    3
[15,]   3    3
[16,]   3    3
[17,]   3    3
[18,]   3    3
[19,]   3    3
[20,]   3    3
> (tab=table(X2G,newG))
   newG
X2G 1 2 3
  1 5 0 0
  2 0 7 1
  3 0 0 7
> sum(diag(prop.table(tab)))
[1] 0.95
> predict(qd,data.frame(Q=8,C=7.5,P=65)) #判定
$`class`
[1] 2
Levels: 1 2 3

$posterior
        1     2       3
1 0.00822 0.992 0.00024

> 

 

Bayes判别准则

线性判别和距离判别的计算相对简单明确，比较实用，但存在两个缺点

一是判别方法与总体各自出现的概率大小完全无关：

二是判别方法与错判后造成的损失无关，这是不尽合理的。

Bayes判别对多个总体的判别考虑的不只是建立判别式，还要计算新样品属于个总体的条件概率p(j/x),j = 1,2,3,4,5...k。比较k个概率的大小，然后将新样品判归为来自概率最大的总体。Bayes判别准则是以个体归属于某类的概率（或某类的判别函数值）最大或错判总平均损失最小为标准的。

什么是先验概率

先验概率（prior probability）是指根据以往经验和分析得到的概率，如全概率公式，它往往作为"由因求果"问题中的"因"出现的概率。就是我们观测数据，大概每个分类所占比例形成的概率分布。

先验概率取相等

> (ld1=lda(X2G~Q+C+P,prior=c(1,1,1)/3)) #
Call:
lda(X2G ~ Q + C + P, prior = c(1, 1, 1)/3)

Prior probabilities of groups:
        1         2         3 
0.3333333 0.3333333 0.3333333 

Group means:
         Q        C      P
1 8.400000 5.900000 48.200
2 7.712500 7.250000 69.875
3 5.957143 3.714286 34.000

Coefficients of linear discriminants:
          LD1         LD2
Q -0.92307369  0.76708185
C -0.65222524  0.11482179
P  0.02743244 -0.08484154

Proportion of trace:
   LD1    LD2 
0.7259 0.2741 
>

> Z1=predict(ld1)#预测所属类别  
> cbind(X2G,round(Z1$x,3),newG=Z1$class)#显示结果 
   X2G    LD1    LD2 newG
1    1 -0.408  2.378    1
2    1 -2.403  0.334    1
3    1 -0.509  1.414    1
4    1 -0.958  0.250    1
5    1 -1.787  0.843    1
6    2 -2.542  0.856    1
7    2  0.749 -2.292    2
8    2 -2.394 -0.969    2
9    2 -1.046 -0.732    2
10   2 -1.350 -2.760    2
11   2 -0.764 -2.785    2
12   2  0.047 -0.771    2
13   2  0.384  0.114    3
14   3  2.772  1.148    3
15   3  1.620  0.072    3
16   3  0.845 -0.270    3
17   3  3.105 -0.115    3
18   3  2.308  0.148    3
19   3  2.313 -0.194    3
20   3  1.581  0.077    3
> 

正常的分布应该是只有中轴有数据

> table(X2G,Z1$class)#混淆矩阵
   
X2G 1 2 3
  1 5 0 0
  2 1 6 1
  3 0 0 7
> round(Z1$post,3) #ld1模型后验概率
       1     2     3
1  0.983 0.006 0.012
2  0.794 0.206 0.000
3  0.937 0.043 0.020
4  0.654 0.337 0.009
5  0.905 0.094 0.000
6  0.928 0.072 0.000
7  0.003 0.863 0.133
8  0.177 0.822 0.000
9  0.185 0.811 0.005
10 0.003 0.997 0.000
11 0.002 0.997 0.001
12 0.111 0.780 0.109
13 0.292 0.325 0.383
14 0.001 0.000 0.999
15 0.012 0.023 0.965
16 0.079 0.243 0.678
17 0.000 0.000 1.000
18 0.001 0.003 0.996
19 0.001 0.004 0.995
20 0.014 0.025 0.961
> 

 因为待估值落在2的概率为69%，所以将其分为2类

> predict(ld1,data.frame(Q=8,C=7.5,P=65))  # ld1模型的判定
$`class`
[1] 2
Levels: 1 2 3
$posterior
         1         2           3
1 0.300164 0.6980356 0.001800378
$x
        LD1        LD2
1 -1.426693 -0.5046594
> 

先验概率取不相等

> (ld2=lda(X2G~Q+C+P,prior=c(5,8,7)/20)) #
Call:
lda(X2G ~ Q + C + P, prior = c(5, 8, 7)/20)

Prior probabilities of groups:
   1    2    3 
0.25 0.40 0.35 

Group means:
         Q        C      P
1 8.400000 5.900000 48.200
2 7.712500 7.250000 69.875
3 5.957143 3.714286 34.000

Coefficients of linear discriminants:
          LD1         LD2
Q -0.81173396  0.88406311
C -0.63090549  0.20134565
P  0.01579385 -0.08775636

Proportion of trace:
   LD1    LD2 
0.7403 0.2597 
>

> cbind(X2G,round(Z2$x,3),newG=Z2$class)#显示结果
   X2G    LD1    LD2 newG
1    1 -0.141  2.583    1
2    1 -2.392  0.825    1
3    1 -0.370  1.642    1
4    1 -0.971  0.548    1
5    1 -1.713  1.247    1
6    2 -2.459  1.362    1
7    2  0.379 -2.200    2
8    2 -2.558 -0.467    2
9    2 -1.190 -0.413    2
10   2 -1.764 -2.382    2
11   2 -1.187 -2.486    2
12   2 -0.112 -0.599    2
13   2  0.340  0.233    3
14   3  2.846  0.937    3
15   3  1.559  0.026    3
16   3  0.746 -0.209    3
17   3  3.006 -0.359    3
18   3  2.251  0.009    3
19   3  2.211 -0.331    3
20   3  1.521  0.036    3
> 

> table(X2G,Z2$class)#混淆矩阵
   
X2G 1 2 3
  1 5 0 0
  2 1 6 1
  3 0 0 7
> round(Z2$post,3) #ld2模型后验概率
       1     2     3
1  0.975 0.009 0.016
2  0.707 0.293 0.000
3  0.907 0.067 0.027
4  0.542 0.447 0.011
5  0.857 0.143 0.001
6  0.889 0.111 0.000
7  0.002 0.879 0.119
8  0.119 0.881 0.000
9  0.124 0.871 0.004
10 0.002 0.998 0.000
11 0.001 0.998 0.001
12 0.074 0.825 0.101
13 0.216 0.386 0.398
14 0.001 0.000 0.999
15 0.009 0.026 0.965
16 0.056 0.274 0.670
17 0.000 0.000 1.000
18 0.001 0.003 0.996
19 0.001 0.005 0.994
20 0.010 0.029 0.961
> 

> predict(ld2,data.frame(Q=8,C=7.5,P=65))  # ld2模型的判定
$`class`
[1] 2
Levels: 1 2 3
$posterior
          1        2           3
1 0.2114514 0.786773 0.001775594
$x
        LD1        LD2
1 -1.537069 -0.1367865
> 

判别分析小结

***敲完时突然不能保存了，前功尽弃，索性直接截图