【深度学习】Python实现2层神经网络的误差反向传播法学习
前言
基于计算图的反向传播详解一篇中,我们通过计算图的形式详细介绍了构建神经网络需要的层,我们可以将其视为组件,接下来我们只需要将这些组件组合起来就可以实现误差反向传播法。
首先我们回顾下神经网络的学习步骤如下:
- 从训练数据中随机选择一部分数据(mini-batch)
- 计算损失函数关于各个权重参数的梯度
- 将权重参数沿梯度方向进行微小的更新
- 重复以上步骤
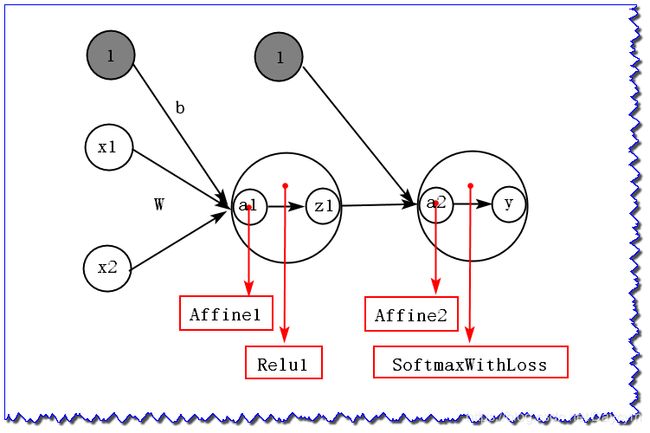
下图为2层神经网络,图中红色表示每层的名称,每层只画了固定的神经元数,主要为了让大家知道层级关系,以便后面进行层的连接
Affine层、Relu层以及SoftmaxWithLoss层实现代码
import numpy as np
# softmax函数
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # 溢出对策
return np.exp(x) / np.sum(np.exp(x))
# 交叉熵误差
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 监督数据是one-hot-vector的情况下,转换为正确解标签的索引
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
# 数值微分(这里加上这个是为了后面对比数值微分和误差反向传播两种方法求的梯度之间的误差)
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
it.iternext()
return grad
class Affine:
def __init__(self, W, b):
self.W =W
self.b = b
self.x = None
self.original_x_shape = None
# 权重和偏置参数的导数
self.dW = None
self.db = None
def forward(self, x):
# 对应张量
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape) # 还原输入数据的形状(对应张量)
return dx
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
class SoftmaxWithLoss:
def __init__(self):
self.loss = None
self.y = None # softmax的输出
self.t = None # 监督数据
def forward(self, x, t):
self.t = t
self.y = softmax(x) # 调用softmax函数
self.loss = cross_entropy_error(self.y, self.t) # 调用cross_entropy_error函数
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况
dx = (self.y - self.t) / batch_size
else:
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx = dx / batch_size
return dx
误差反向传播法的神经网络的实现
# coding: utf-8
import numpy as np
from collections import OrderedDict
# 2层神经网络的实现类
class TwoLayerNet:
# input_size输入层的神经元数、hidden_size隐藏层神经元数、output_size输出层神经元数
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 初始化权重
self.params = {} # 参数字典
# 初始化输入层到隐藏层的权重、偏置
# 随机生成形状为(input_size, hidden_size)的二维数组
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
# 生成和隐藏层神经元数相同的一维0数组
self.params['b1'] = np.zeros(hidden_size)
# 初始化隐藏层到输出层的权重、偏置
# 随机生成形状为(hidden_size, output_size)的二维数组
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 生成层
self.layers = OrderedDict() # 创建有序字典(可以记住向字典中添加元素的顺序,在反向传播时只需要按相反的顺序调用各层即可)
# 以正确的顺序连接各层
# Affine1层
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
# Relu1层
self.layers['Relu1'] = Relu()
# Affine2层
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
# SoftmaxWithLoss层
self.lastLayer = SoftmaxWithLoss()
# 进行识别(推理)
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# 计算损失函数的值 x:输入数据, t:监督数据
def loss(self, x, t):
y = self.predict(x) # 预测
return self.lastLayer.forward(y, t)
# 计算识别精度
def accuracy(self, x, t):
y = self.predict(x) # 推理
y = np.argmax(y, axis=1) # 返回最大值的索引
if t.ndim != 1 : t = np.argmax(t, axis=1)
# 如果索引相等,即识别正确,计算精度
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# 计算权重参数梯度 x:输入数据, t:监督数据
# 通过误差反向传播法计算关于权重的梯度
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'] = self.layers['Affine1'].dW
grads['b1'] = self.layers['Affine1'].db
grads['W2'] = self.layers['Affine2'].dW
grads['b2'] = self.layers['Affine2'].db
return grads # 返回各个参数的梯度
# 计算权重参数梯度 x:输入数据, t:监督数据
# 通过数值微分计算(用于对比)
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads # 返回各个参数的梯度
像这样通过将每层的组件,按照顺序连接起来,可以轻松地构建神经网络
这样,无论是5层、10层、20层 ······,只需要将组件连接起来即可
梯度确认
import mnist
# 读入数据
(x_train, t_train), (x_test, t_test) = mnist.load_mnist(normalize=True, one_hot_label=True)
# 构建神经网络
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
# 使用部分数据
x_batch = x_train[:3]
t_batch = t_train[:3]
# 计算梯度
# 数值微分
grad_numerical = network.numerical_gradient(x_batch, t_batch)
# 误差反向传播法
grad_backprop = network.gradient(x_batch, t_batch)
# 求两种梯度法的梯度误差
for key in grad_numerical.keys():
# 求各个权重参数对应元素的差的绝对值,并计算其平均值
diff = np.average(np.abs(grad_backprop[key] - grad_numerical[key]))
print(key + ":" + str(diff))
输出为:
W1:3.795184189717579e-10
b1:2.495277803749767e-09
W2:4.712630591287661e-09
b2:1.3932517608367112e-07
通过结果,我们可以看出,两种方法的计算结果误差很小,几乎为0
使用误差反向传播法进行神经网络的学习
import time
import mnist
start = time.time()
# 读入数据
(x_train, t_train), (x_test, t_test) = mnist.load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 使用误差反向传播法求梯度
#grad = network.numerical_gradient(x_batch, t_batch)
grad = network.gradient(x_batch, t_batch)
# 更新
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print(train_acc, test_acc)
end = time.time()
print("耗时:", (end-start))
输出为:
0.13911666666666667 0.1393
0.90605 0.9098
0.9235666666666666 0.9256
0.9352666666666667 0.9343
0.9438666666666666 0.9433
0.9513 0.9512
0.9576666666666667 0.9546
0.9592333333333334 0.955
0.9645666666666667 0.9608
0.9674833333333334 0.9619
0.96965 0.9635
0.9711833333333333 0.9654
0.9737166666666667 0.9657
0.9735833333333334 0.9661
0.97765 0.9679
0.9779 0.9693
0.97895 0.9686
耗时: 31.826430082321167
总结
- 数值微分的计算耗时太大,使用误差反向传播法学习大大减小了学习的时间
- 误差反向传播法的实现比数值微分法复杂,容易出错
- 通过比较数值微分的结果和误差反向传播法的结果,以确认误差反向传播法的实现是否正确(梯度确认)
- 误差反向传播法可以高效地求解参数梯度