R语言典型相关分析
参考资料《统计建模与R软件》
典型相关的数学模型
设 X=(X1,X2,…,Xp)T,Y=(Y1,Y2,…,Yq)T 为两条随机向量, 我们希望找到向量 a,b 使得 U=aTX,V=aTY,ρ(U,V)达到最大 ,由于这样的向量有多组,我们加一个约束
Var(U)=Var(V)=1 这就变成了一个规划问题,我们可以求解(证明方法见参考资料P546)
类似的对于 ak,bk,Uk=aTkX,Vk=bkY 使得 maxρ(Uk,Vk),Var(Uk)=Var(VK)=1 成为第 k 个典型相关系数.
计算
令
M1=Σ−111Σ12Σ−122Σ21M2=Σ−122Σ21Σ−111Σ12
相关系数分别为
ρ21≥ρ22≥…,≥ρ2min(p,q) 分别为第 k 个相关系数,他们是 M1,M2 的特征值, ak,bk 为相应的特征向量.
估计
对于样本的相关阵往往不好知道确切值,我们可以计算 Σ 的最大似然估计去计算 M
R语言实现
> test<-data.frame(
+ X1=c(191, 193, 189, 211, 176, 169, 154, 193, 176, 156,
+ 189, 162, 182, 167, 154, 166, 247, 202, 157, 138),
+ X2=c(36, 38, 35, 38, 31, 34, 34, 36, 37, 33,
+ 37, 35, 36, 34, 33, 33, 46, 37, 32, 33),
+ X3=c(50, 58, 46, 56, 74, 50, 64, 46, 54, 54,
+ 52, 62, 56, 60, 56, 52, 50, 62, 52, 68),
+ Y1=c( 5, 12, 13, 8, 15, 17, 14, 6, 4, 15,
+ 2, 12, 4, 6, 17, 13, 1, 12, 11, 2),
+ Y2=c(162, 101, 155, 101, 200, 120, 215, 70, 60, 225,
+ 110, 105, 101, 125, 251, 210, 50, 210, 230, 110),
+ Y3=c(60, 101, 58, 38, 40, 38, 105, 31, 25, 73,
+ 60, 37, 42, 40, 250, 115, 50, 120, 80, 43)
+ )
# 相关分析
> ca <- cancor(scale(test)[,1:3],scale(test)[,4:6])
> ca
$cor #相关系数
[1] 0.79560815 0.20055604 0.07257029
#x的系数
$xcoef
[,1] [,2] [,3]
X1 -0.17788841 -0.43230348 -0.04381432
X2 0.36232695 0.27085764 0.11608883
X3 -0.01356309 -0.05301954 0.24106633
#y的系数
$ycoef
[,1] [,2] [,3]
Y1 -0.08018009 -0.08615561 -0.29745900
Y2 -0.24180670 0.02833066 0.28373986
Y3 0.16435956 0.24367781 -0.09608099
$xcenter
X1 X2 X3
2.289835e-16 4.315992e-16 -1.778959e-16
$ycenter
Y1 Y2 Y3
1.471046e-16 -1.776357e-16 4.996004e-17相关分析变量及系数
> U <- as.matrix(scal_test)[,1:3] %*% ca$xcoef
> V <- as.matrix(scal_test)[,4:6] %*% ca$ycoef
> U
[,1] [,2] [,3]
[1,] -0.009969788 -0.121501078 -0.20419401
[2,] 0.186887139 -0.046163013 0.13223387
[3,] -0.101193522 -0.141661215 -0.37063341
[4,] 0.060964112 -0.346616669 0.03342558
[5,] -0.512831098 -0.458299483 0.44354554
[6,] -0.077780541 0.094512914 -0.23766491
[7,] 0.003955674 0.254201102 0.25701898
[8,] -0.016855040 -0.127105942 -0.34147617
[9,] 0.203734347 0.196310283 -0.00758741
[10,] -0.104800666 0.208124774 -0.11711820
[11,] 0.113834968 -0.016598895 -0.09752299
[12,] 0.063237343 0.213427257 0.21221151
[13,] 0.043586465 -0.008040409 0.01237648
[14,] -0.082181602 0.055998387 0.10021686
[15,] -0.094153311 0.228436101 -0.04670258
[16,] -0.173085857 0.047742282 -0.20173015
[17,] 0.718139369 -0.256090676 0.05898572
[18,] 0.001362964 -0.317746855 0.21374067
[19,] -0.221400693 0.120731486 -0.22201469
[20,] -0.001450263 0.420339649 0.38288931
> V
[,1] [,2] [,3]
[1,] -0.02909460 0.031027608 0.344302062
[2,] 0.23190170 0.084158321 -0.403047146
[3,] -0.12979237 -0.112030106 -0.133855684
[4,] 0.09063830 -0.150034732 -0.059921010
[5,] -0.39173848 -0.209788233 -0.008592976
[6,] -0.11930102 -0.288113119 -0.480186091
[7,] -0.22619839 0.122191086 -0.006091381
[8,] 0.21834490 -0.164740837 -0.074849953
[9,] 0.26809619 -0.165185828 0.003582504
[10,] -0.38258341 -0.041647344 0.042948559
[11,] 0.21737727 0.056375494 0.277291769
[12,] 0.01130349 -0.218167527 -0.264987331
[13,] 0.16412985 -0.065834278 0.157664098
[14,] 0.03462910 -0.097067107 0.157711712
[15,] 0.05393456 0.778658842 -0.283334468
[16,] -0.15965387 0.183746435 0.008766141
[17,] 0.43237930 -0.002016448 0.080198839
[18,] -0.12845980 0.223805116 0.055667431
[19,] -0.31879992 0.059073577 0.277587462
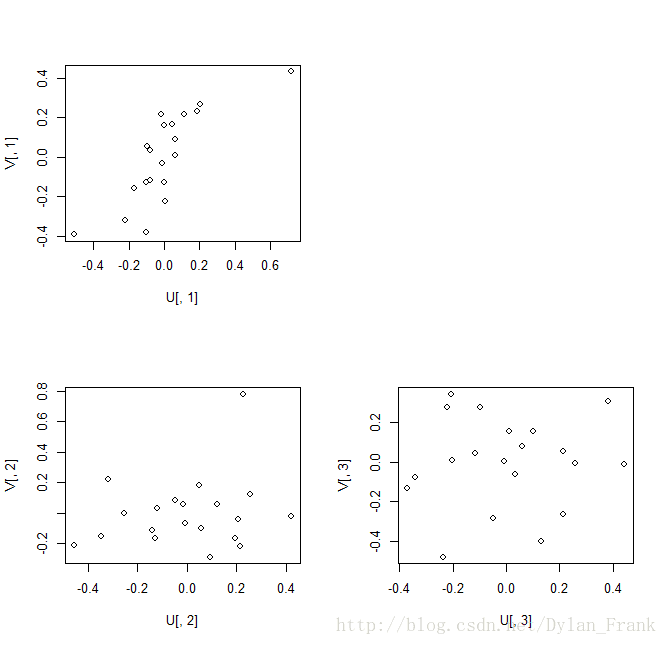
[20,] 0.16288721 -0.024410919 0.309145462画图
可以看出 U[,1]与V[,1] 几乎成线性