《数据结构与算法之美》专栏阅读笔记7——图

有点想知道当年我到底看的什么书，对于树、图有这么深的偏见，直到避而不见。
其实下午忙完后，晒着久违的太阳，捧一杯茶，看着时钟滴答，打算差不多瞅一瞅晚上要看的图（就下班了），就回家缓一下先的，结果前后可能不到二十分钟吧，深度优先遍历和广度优先遍历就无压写出来了……不对啊！这不是跟树的按层遍历一毛一样么~作者讲的真好，快来圈我的钱吧（嗨皮

图

非线性表数据结构，图中的元素称作顶点，顶点之间的连接关系叫做边。

图的表示

以微信示例，每个用户是一个顶点，好友关系就是一条边，每个用户的好友个数对应的就是顶点的度。
以微博示例，微博允许单方面关注，可以使用带方向的边来表示用户之间的关系。
以QQ示例，亲密度的功能表示就可以用带权图来表示，给边加上权值来表示亲密度。
有向图：边是有方向的，一个顶点的边的个数用出度和入度来表示，可以带权值或不带权值。
无向图：边是无方向的，一个顶点的边的个数用度来表示，可以带权值或不带权值。

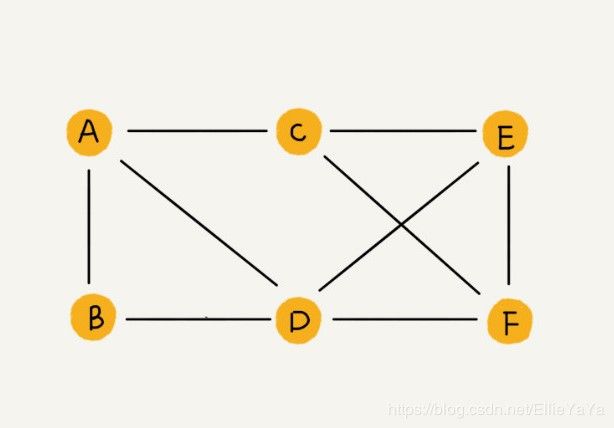图1 无向图

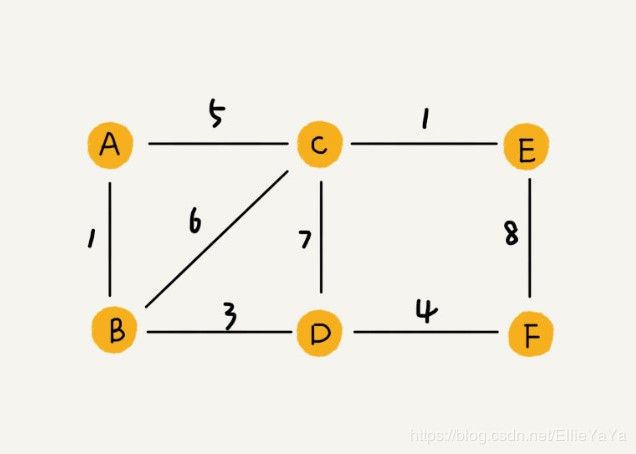图2 有向图

图2 带权图

图的存储

邻接矩阵

因为边是两个点的之间的关系，所以用二维矩阵表示十分直观。

优点：基于数组，效率高。
缺点：空间利用率不高。

邻接表

用链表来存储每个顶点的邻接点。

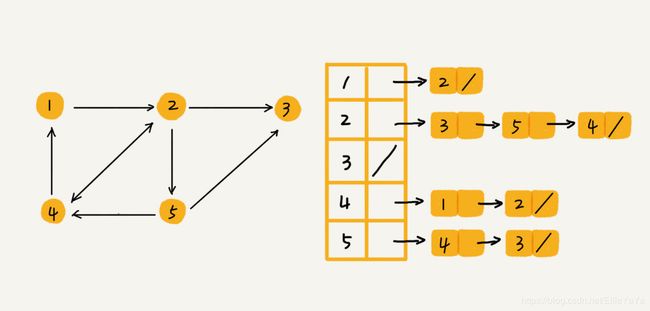
缺点：链过长的时候效率较低。
可以将链表换成其他效率较高的数据结构。

开篇思考题的中有一条，如何查看用户的粉丝列表，解答中给出建立逆邻接表。其实就是对于有向图，出度和入度都记录。

表的查找

是对使用邻接表方式存储的图进行搜索。

public class Graph {
    private int size;
    private LinkedList adj[];  // 邻接表

    public Graph(int size) {
        this.size = size;
        adj = new LinkedList[size];
        for (int i = 0; i < size; i++) {
            adj[i] = new LinkedList<>();
        }
    }

    public void addEdge(int s, int t) {
        adj[s].add(t);
        adj[t].add(s);
    }
}

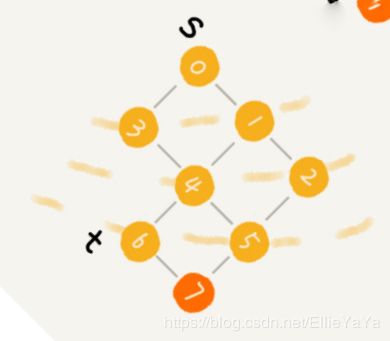
广度优先搜索BFS

根据由近到远的方式进行搜索。

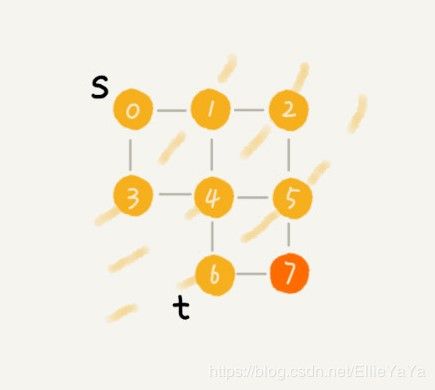
转一下是不是就是一棵树的深度遍历？
我自己在写的时候就是按照这个思路来的，最后发现这个作者写的差不多，这里就分解一下步骤而已。
1、按照树的按层遍历来查找
和树的区别在于，下一层节点之间会有连接，所以需要对已经遍历过的节点做个标记，避免重复遍历（转圈出不来）。同样地，用队列来进行按“层”查找。

public void BFS(int s, int t) {
        if (s == t)
            return;

        // find t
        boolean[] visited = new boolean[size];
        visited[s] = true;
        Queue queue = new LinkedList();
        queue.add(s);

        while (!queue.isEmpty()) {
            int vertex = queue.poll();
            int adjSize = adj[vertex].size();
            for (int i = 0; i < adjSize; i++) {
                int adjVertex = adj[vertex].get(i);
                if (!visited[adjVertex]) {
                    if (adjVertex == t) {
                        return;
                    }
                    queue.add(adjVertex);
                    visited[adjVertex] = true;
                }
            }
        }
    }

是不是一毛一样。然后就是很尴尬的一幕：找到之后干啥？
图一般是用来找最短路径丫啥的，所以是需要是需要进路查找路径的，这个地方一开始想着按照遍历的顺序来记录，会很别扭，不知道怎么搞。（不管有没有找到都会遍历，都会被记录）
借鉴逆邻接表的思路，记录路径的时候是往前找，“下一层找谁是不确定的，而且有多个，但是从哪里找到当前元素是确定的（每个顶点只会被遍历一次）”，所以记录来处即可。
因此，用来打印的函数如下：

private void printPath(int[] path, int s, int t) {
        if (path[t] != -1 && path[t] != s) {
            printPath(path, s, path[t]);
        }
        System.out.print(t + " ");
    }

加到查找逻辑中如下：

public void BFS(int s, int t) {
        if (s == t)
            return;

        // find t
        boolean[] visited = new boolean[size];
        visited[s] = true;
        Queue queue = new LinkedList();
        queue.add(s);

        // record path
        int[] path = new int[size];
        for (int i = 0; i < size; i++) {
            path[i] = -1;
        }

        while (!queue.isEmpty()) {
            int vertex = queue.poll();
            int adjSize = adj[vertex].size();
            for (int i = 0; i < adjSize; i++) {
                int adjVertex = adj[vertex].get(i);
                if (!visited[adjVertex]) {
                    path[adjVertex] = vertex;
                    if (adjVertex == t) {
                        printPath(path, s, t);
                        return;
                    }

                    queue.add(adjVertex);
                    visited[adjVertex] = true;
                }
            }
        }
    }

深度优先搜索 DFS

总结一下就是：一条道走到黑，不行就转头走没走过的路。

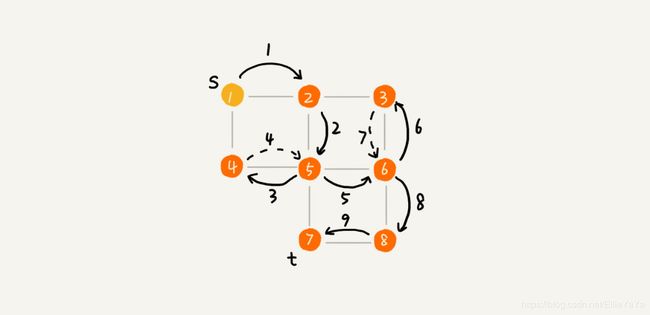
一条道走到黑，把每条道都走到黑。其实很明显就是递归。
实现如下：

private boolean hasFound = false;
    public void DFS(int s, int t) {
        hasFound = false;
        // find t
        boolean[] visited = new boolean[size];
        visited[s] = true;

        // record path
        int[] path = new int[size];
        for (int i = 0; i < size; i++) {
            path[i] = -1;
        }

        recurDfs(s, t, visited, path);
        printPath(path, s, t);
    }

    private void recurDfs(int s, int t, boolean[] visited, int[] path) {
        if (hasFound)
            return;

        int adjSize = adj[s].size();
        for (int i = 0; i < adjSize; i++) {
            int adjVertex = adj[s].get(i);
            if (!visited[adjVertex]) {
                path[adjVertex] = s;
                if (adjVertex == t) {
                    hasFound = true;
                    break;
                }

                visited[adjVertex] = true;
                recurDfs(adjVertex, t, visited, path);
            }
        }
    }

就是在BFS的基础上改一下变成递归（不用队列来控制按层遍历就行），写法上和作者有一点点区别，但是测试效果是一致的。作者代码如下：

课后思考

关于如何将迷宫抽象成图，看评论说是分岔点对应图的顶点。我一开始想的是每个死胡同的点是顶点，视觉上是边的长度不一样？仔细想一下，如果是用DFS来查找的话，就是回溯点不一样，按照分岔点对应顶点的方式感觉上走的回头路少一点？但是用DFS来找，按照死胡同点对应顶点，会简化很多。