The Graph Neural Network Model论文学习笔记
The Graph Neural Network Model论文学习
- 摘要
- 1.简介
- 2.图神经网络模型
- A.模型
- B. 状态计算
- C. 学习算法
- D. 转移和输出函数的实现
- E.和Random Walks及RNN的比较
原文链接
摘要
诸如计算机视觉、分子化学、模式识别、数据挖掘等许多科学和工程领域中的数据间的潜在关系可以用图来表示。本文提出一种新的神经网络模型——图神经网络模型——对现有的神经网络模型进行了拓展,适用于处理可以表示为图的数据。该模型实现了一个将图 G G G和图中的某个节点 n n n映射到 m m m维欧式空间的函数 τ ( G , n ) ∈ R m \tau(G,n)\in\mathbb{R^m} τ(G,n)∈Rm,可以直接处理大部分实用的图类型,例如无环、有环、无向、有向图。接着,推导了用于计算所提出GNN模型参数的有监督学习算法,并分析了该算法的计算代价。最后,通过实验验证所提出学习算法,并展示其泛化能力。
1.简介
在许多领域中,数据可以直接用图结构来表示。最简单的图结构是单一节点和序列。但是,在许多应用中,数据是以更复杂的图结构组织的,例如树、无环图、有环图。
在机器学习中,结构化数据通常和这样一个目标相关,即从样本数据中学习将图 G G G和图中的某个节点 n n n映射到 m m m维欧式空间的函数 τ ( G , n ) ∈ R m \tau(G,n)\in\mathbb{R^m} τ(G,n)∈Rm。图形领域的应用大体可以分为两大类:1) graph-focused;2) node-focused。在graph-focused的应用中,函数 τ \tau τ和节点 n n n是独立的,即 τ ( G , n ) \tau(G,n) τ(G,n)变为 τ ( G ) \tau(G) τ(G), τ \tau τ实现一个分类器或回归器。在node-focused的应用中,函数 τ \tau τ和节点 n n n是相关的,因此分类取决于每个节点的属性。
传统的机器学习方法通过将图结构化信息映射为简单的表征的预处理过程来处理图结构化数据。换言之,预处理就是现将图结构化数据“压缩”进实值向量,然后使用基于列的数据处理技术处理。但是,预处理会丢失很多重要的信息,并对最总结果有影响。最近,存在各种试图在处理阶段之前保持数据的图形结构性质的方法。该想法是使用图的节点之间的拓扑关系对底层图结构化数据进行编码,以便在数据处理步骤中结合图结构化信息。循环神经网络(RNN)和马尔科夫链就属于这类方法,并配广泛应用于 graph-focused和node-focused的问题中。本文提出的方法扩展了这两种方法,因为它可以直接处理图形结构化信息。
本文提出一个有监督神经网络模型,该模型适用于graph-focused和node-focused应用。这个模型将连个现存的模型统一成一个通用的结构。我们将这种新的模型称为图神经网络模型(GNN)。我们将看到GNN是循环神经网络(RNN)和random
walk models的扩展,同时也保留的二者的特点。该模型扩展RNN是因为它可以处理更加广泛的图类型,包括有向、无向图,也可以不需要任何预处理步骤来处理node-focused应用。该模型通过引入学习算法和扩大可以建模的过程类别来扩展random walk theory。
GNN基于信息扩散机制。图由一组单元(units)处理,每个单元对应图中的一个节点,节点根据图的连接互连。这些单元跟新它们的状态并交换信息,直到它们到大稳定均衡状态。然后,基于节点状态,GNN的输出在每个节点局部计算。为了确保唯一的稳定均衡总是存在,扩散机制是受限的。这种实现机制已经用于细胞神经网络和Hopfield神经网络。
本文中介绍一种学习算法,该算法在一组给定的训练样本上估计GNN模型的参数。此外,参数估计算法的计算代价也会考虑。
2.图神经网络模型
首先,介绍一些贯穿全文使用的符号。
| 符号 | 说明 |
|---|---|
| N N N | 节点集合 |
| E E E | 边集合 |
| n e [ n ] ne[n] ne[n] | 节点n的邻点 |
| c o [ n ] co[n] co[n] | 与节点n相连的边集合 |
图可以定义为 G = ( N , E ) G=(N,E) G=(N,E),节点和边可能有用实向量表示的标签,节点n的标签表示是为 l n ∈ R l N l_n\in\mathbb{R}^{l_N} ln∈RlN,边 ( n 1 , n 2 ) (n_1,n_2) (n1,n2)的标签表示为 l n 1 , n 2 ∈ R l E l_{n_1,n_2}\in\mathbb{R}^{l_E} ln1,n2∈RlE。设 l l l表示通过将图的所有标签堆叠在一起而获得的向量。标签采用的符号遵循更一般的方案:如果 y y y是包含图中数据的向量,并且 S S S是节点(边)的子集,那么 y S y_S yS表示通过从 y y y中选择与 S S S中的节点(边)相关的分量而获得的向量。例如, l n e [ n ] l_{ne[n]} lne[n]表示包含节点n的所有邻点的标签向量。标签通常包含关于节点对象的特征和对象间的关系特征。如下图中的房子,节点属性可能表示的是区域的属性(例如,面积、周长、平均色彩强度),而边属性可能表示的区域的相对位置(例如,区域重心间的距离、主轴间的角度)。对边没有设定,有向、无向、有环、无环都是被允许的。但是,当不同类别的边同时存在同一个数据集中,有必要区分它们。这可以通过对每个边附加一个合适的标签来轻易的解决。这种情况下,不同的边变成了携带不同标签的边。
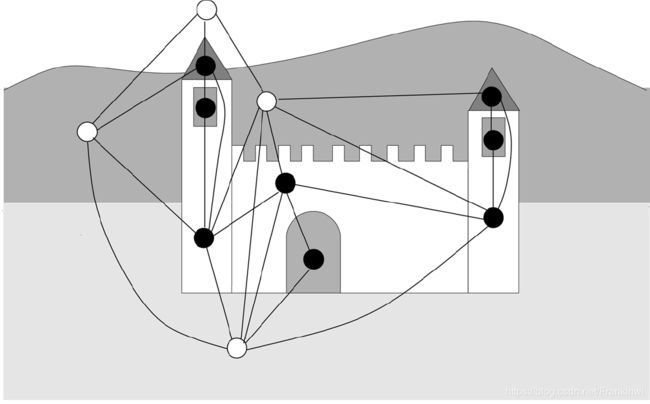
所考虑的图可以是位置的(positional)或者非位置的(nonpositional)。目前位置讨论的都是nonpositional的图。positional图的不同之处是节点 n n n的所有邻点都有一个用于表示其逻辑位置的整数标识,即存在一个映射函数 v n v_n vn,将节点 n n n的所有邻点 n e [ n ] ne[n] ne[n] 映射为标识 { 1 , 2 , . . . , ∣ N ∣ } \{1,2,...,|N|\} {1,2,...,∣N∣},这些标识给节点 n n n的每一个邻点 u u u设置一个位置 v n ( u ) v_n(u) vn(u)。注意,邻点的顺序可以隐式地用来存储有用的信息。如上图, v n v_n vn以类似钟表顺序的形势来枚举节点 n n n的邻点。
本文考虑到域 D = G × N \mathcal D=\mathcal{G \times N} D=G×N, G \mathcal G G是图集合, N \mathcal N N是图集合的节点的子集。我们假设一个带有学习集的监督学习框架

A.模型
所提出方法的直观思想是图中的节点表示对象或概念,而边表示它们的关系。 每个概念都由其特征和相关概念自然定义。因此,可以给每个节点 n n n附加一个状态 x n ∈ R s x_n\in\mathbb{R^s} xn∈Rs,该状态基于节点 n n n的邻点所包含的信息,如下图。

| 符号 | 说明 | 功能 |
|---|---|---|
| f w f_w fw | 局部转移函数(local transition function) | 表示节点 n n n和其邻点的依赖 |
| g w g_w gw | 局部输出函数(local output function) | 输出怎么产生 |

从公式(1)看出,状态 x n x_n xn是根据节点 n n n的标签、与节点n相连的边的标签 l c o [ n ] l_{co[n]} lco[n]、节点 n n n的所有邻点状态 x n e [ n ] x_{ne[n]} xne[n]和所有节点n的领点的标签 l n e [ n ] l_{ne[n]} lne[n]相关。输出 o n o_n on与节点 n n n的状态 x n x_n xn和标签 l n l_n ln相关。
备注1: 公式(1)可以简化。例如:可以将公式(1)中的 l n e [ n ] l_{ne[n]} lne[n]去掉,因为 x n e [ n ] x_{ne[n]} xne[n]中已经包含了 l n e [ n ] l_{ne[n]} lne[n]的信息。本文注重讨论无简化的情况。
备注2: 公式(1)是用于无向图的。当处理有向图时,函数 f w f_w fw 可以将边的方向表征作为一个输入,例如, d l = 1 d_l=1 dl=1表示边指向节点 n n n, d l = 0 d_l=0 dl=0表示边从节点 n n n射出。后续中,除了明确声明,本文所有的结果也适用于有向图和有向无向混合图。
备注3: 通常, f w f_w fw 和 g w g_w gw以及它们的参数可能依赖节点 n n n。不同的实现机制用来表示不同的对象类别。这种情况下,每种类别的节点 k n k_n kn有其特定的转移函数 f k n f^{k_n} fkn和输出函数 g k n g^{k_n} gkn。但是,为了简明,本文的分析将公式(1)当作是所有节点共享同一种实现的特定模型。
公式(1)的紧凑形式如下:

F w F_w Fw是全局转移函数, G w G_w Gw是全局输出函数。全局函数是将 f w f_w fw 和 g w g_w gw的 ∣ N ∣ |N| ∣N∣个实例堆叠起来的形式。
现在,我们感兴趣的是什么时候可以唯一确定 x x x和 o o o,并且公式(2)定义一个 D \mathcal D D到 R m \mathbb{R}^m Rm的映射 φ w \varphi_w φw,该映射将图作为输入,对每个节点返回一个输出 o n o_n on。根据Banach不动点定理, F w F_w Fw是状态的压缩映射时,公式(2)有唯一解。后文,我们将表明可以通过合适的转移函数实现来确保 F w F_w Fw是压缩映射这一性质。
对于非位置图,公式(1)中的 f w f_w fw可以化为公式(3):
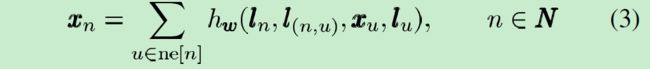
h w h_w hw是一个参数化函数。这个已经在RNN中成功应用的转移函数不受子节点的位置和数量影响。后文中,将(3)称为非位置形式,(1)称为位置形式。为了实现GNN模型,需要提供以下几项:
- 解决公式(1)的方法
- 使用来自训练数据集的示例来学习 f w f_w fw 和 g w g_w gw的学习算法
- f w f_w fw 和 g w g_w gw的一种实现
B. 状态计算
Banach不动点定理不仅保证了公式(1)解的存在和唯一性,也提供了一种计算状态的迭代策略:

公式(4)对任意初始值 x ( 0 ) x(0) x(0)以指数级速度收敛到公式(2)的解。因此,可以把 x ( t ) x(t) x(t)当作是通过转移函数 F w F_w Fw更新的状态。事实上,公式(4)为求解非线性方程实现了一个Jacobi迭代方法。因此,输出和状态可以迭代计算:

类似于公式(5)这样的网络称为编码网络(encoding network)。为了构造编码网络,图的每个节点被替换为计算 f w f_w fw函数的单元,如下图。

每个单元存储节点 n n n的当前状态 x n ( t ) x_n(t) xn(t),并且,当单元被激活时,将使用节点标签和邻点存储的信息计算新的状态 x n ( t + 1 ) x_n(t+1) xn(t+1)。单元的同时和重复激活产生了公式()5所描述的行为。另一个实现函数 g w g_w gw的单元产生节点 n n n的输出。
当 f w f_w fw和 g w g_w gw通过前馈神经网络实现时,编码网络就变成了RNN,其中的网络连接连接可以分成内部和外部连接。内部连接由用于实现该单元的神经网络结构确定。外部连接取决于已处理图形的边。
C. 学习算法
在GNN中学习包括估计参数 w \mathcal w w,使得 φ w \varphi_{\mathcal w} φw近似于学习数据集中的数据
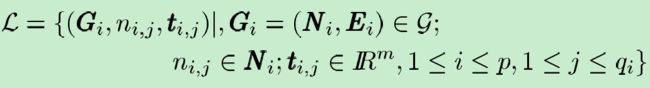
其中, q i q_i qi是图 G i G_i Gi中有监督节点的个数。对graph-focused的任务,一个特殊节点用于目标( q i = 1 q_i=1 qi=1,表示图 G i G_i Gi只有一个监督节点);而对node-focused的任务,原则上每个节点都可以有监督(这里可以理解为 1 ≤ q i ≤ ∣ N i ∣ 1\leq q_i\leq |N_i| 1≤qi≤∣Ni∣)。学习任务可以看做是最小化如下的二次代价函数

备注4: 在神经网络应用中很常见,代价函数可能包含惩罚项来控制模型的其他性质。例如,代价函数可能包含一个平滑因子(smoothing factor)来惩罚任何输出突变和提升泛化性能。
学习算法基于梯度下降策略,并包含以下几个步骤:
a) 状态 x n ( t ) x_n(t) xn(t)有公式(5)迭代更新直到在T时刻到达公式(2)的不动点解,即 x ( T ) ≈ x x_(T)\approx x x(T)≈x
b) 计算梯度 ∂ e w ( T ) / ∂ w \partial{e_w(T)}/ \partial{w} ∂ew(T)/∂w
c) 根据b)步骤中计算的梯度更新权值 w w w
步骤a)中, F w F_w Fw是压缩映射的假设将保证收敛到不动点解。步骤c)使用传统的梯度下降。后面将看到,步骤b) 可以通过利用GNN中发生的扩散过程以非常有效的方式进行。有趣的是,这个扩散过程和RNN中的非常类似,梯度计算时通过反向传播算法进行的。
本文基于Almeida–Pineda算法,给出一个有效计算梯度的方法。因为公式(5)在梯度计算前已经到达了稳定点 x x x,可以假设对任意 t ≥ t 0 t\geq t_0 t≥t0的时刻, x ( t ) = x x(t)=x x(t)=x成立。因此,反向传播可以通过仅存储 x x x来实现。接下来的两个定理证明这个直观方法,具体证明参考原文。
- 定理1:证明可微。
- 定理2:证明反向传播。
下表给出学习算法:

算法包含主程序和前馈FORWARE和反馈BACKWARD函数。FORWARE函数的输入是当前参数 w w w的集合,并不断的迭代寻找收敛点。迭代的终止条件是当相邻的两次状态值的差 ∣ ∣ x ( t ) − x ( t − 1 ) ∣ ∣ ||x(t)-x(t-1)|| ∣∣x(t)−x(t−1)∣∣比给定的阈值 ε f \varepsilon_f εf小,即 ∣ ∣ x ( t ) − x ( t − 1 ) ∣ ∣ ≤ ε f ||x(t)-x(t-1)||\leq{\varepsilon_f} ∣∣x(t)−x(t−1)∣∣≤εf时。BACKWARD函数计算梯度:公式(7)不停的迭代直到 ∣ ∣ z ( t − 1 ) − z ( t ) ∣ ∣ ≤ ε b ||z(t-1)-z(t)||\leq{\varepsilon_b} ∣∣z(t−1)−z(t)∣∣≤εb为止;然后公式(8)计算出梯度。
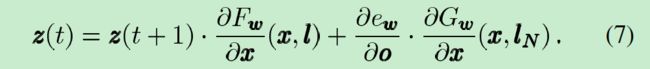
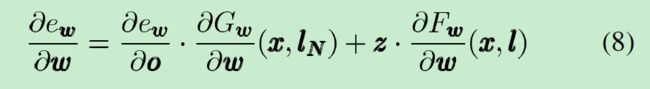
主函数不停地更新权值直到输出满足期望的准确度或者满足其他的终止条件。 λ \lambda λ是提前定义的学习率,其他的基于梯度下降策略的通用策略也可以使用,例如我们使用动量项(momentum term)和自适应学习率策略。在我们的GNN仿真器中,权值是通过resilient back-propagation策略更新的。另一方面,为GNN设计不明确依赖梯度的学习算法目前不明显,这也是未来需要研究的。事实上,编码网络仅明显的和静态前馈网络类似,因为,根据输入图的拓扑结构,层的数量是动态确定的、权值是部分共享的。因此,二阶学习算法、剪枝等为静态网络设计的方法不能直接对GNN使用。
D. 转移和输出函数的实现
局部输出函数 g w g_w gw的实现不需要满足任何特定的限制。在GNN中, g w g_w gw是一个多层的前馈神经网络。另一方面,局部转移函数 f w f_w fw在提出的模型中扮演重要的角色,因为它的实现决定了公式(1)的解的数量和存在性。GNN后的假设是: f w f_w fw的设计是使全局转移函数 F w F_w Fw关于状态 x x x的压缩映射。接下来我们描述使用不同策略满足这个目的的两个神经网络模型。
1)线性(非位置化)GNN。公式(3)可以用下式实现:
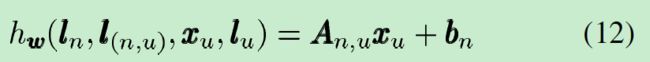
向量 b n b_n bn和矩阵 A n , u A_{n,u} An,u是由两个前馈神经网络(FNN)决定的,这两个FNN的参数和GNN的一致。更加准确的说,将产生 A n , u A_{n,u} An,u的FNN网络称为transition network,将产生 b n b_n bn的另一个FNN网络称为forcing network。此外,令 ϕ w \phi_w ϕw是 R 2 l N + l E → R s 2 \mathbb R^{2l_N+l_E} \rightarrow{\mathbb R^{s^2}} R2lN+lE→Rs2的函数映射, ρ w \rho_w ρw是 R l N → R s \mathbb R^{l_N} \rightarrow{\mathbb R^s} RlN→Rs的函数映射,然后我们用下式定义 b n b_n bn和 A n , u A_{n,u} An,u:
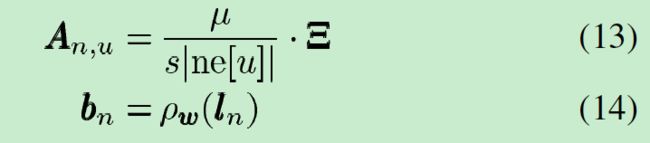
公式(13)中 μ \mu μ的取值范围是 ( 0 , 1 ) (0,1) (0,1)之间, Ξ = r e s i z e ( ϕ w ( l n , l ( n , u ) , l u ) ) \Xi = resize(\phi_w(l_n,l_{(n,u)},l_u)) Ξ=resize(ϕw(ln,l(n,u),lu)),resize(.)表示将 ϕ w ( l n , l ( n , u ) , l u ) \phi_w(l_n,l_{(n,u)},l_u) ϕw(ln,l(n,u),lu)的输出从 s 2 s^2 s2维度的向量转变为 s × s s\times s s×s的矩阵。因此, A n , u A_{n,u} An,u是通过将转移网络 ϕ w \phi_w ϕw的输出放进一个方阵中,然后再乘以一个 μ / s ∣ n e [ u ] ∣ \mu/s|ne[u]| μ/s∣ne[u]∣因子。另一方面, b n b_n bn只是forcing network的输出向量。这里进一步假设 ∣ ∣ ϕ w ( l n , l ( n , u ) , l u ) ∣ ∣ 1 ≤ s ||\phi_w(l_n,l_{(n,u)},l_u)||_1 \leq s ∣∣ϕw(ln,l(n,u),lu)∣∣1≤s成立,如果转移网络的输出神经元使用有界的激活函数,那么这个假设很容易证明。在这种情况下, F w ( x , l ) = A x + b F_w(x,l)=Ax+b Fw(x,l)=Ax+b, b b b是通过将所有的 b n b_n bn堆叠起来的向量, A A A是一个块矩阵 { ‾ A ‾ n , u } \underline \{\overline A_{n,u}\} {An,u},当 u u u是 n n n的领点时, A ‾ n , u = A n , u \overline A_{n,u} = A_{n,u} An,u=An,u,否则 A ‾ n , u = 0 \overline A_{n,u} = 0 An,u=0。此外,向量 b n b_n bn和矩阵 A n , u A_{n,u} An,u不依赖于状态 x x x,只依赖节点和边的标签。因此, ∂ F w / ∂ x = A \partial{F_w}/ \partial{x} = A ∂Fw/∂x=A,通过简单的线性代数,可证明下式,从而表明了 F w F_w Fw是压缩映射。
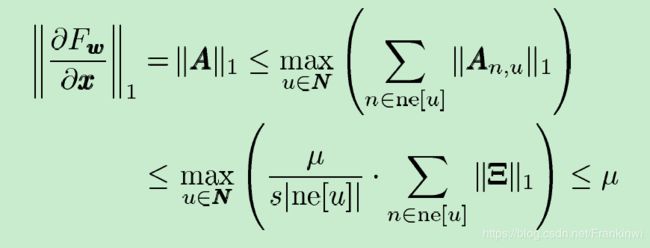
1)非线性(非位置化)GNN。在这种情况下, h w h_w hw是由多层FNN实现的。由于三层的神经网络是一个通用的逼近器, h w h_w hw可以近似任何期望的函数。然而,并不是所有的参数 w w w都会被使用,必须保证相应的转移函数 F w F_w Fw是压缩映射。这可以通过给公式(6)添加惩罚项来满足,例如:
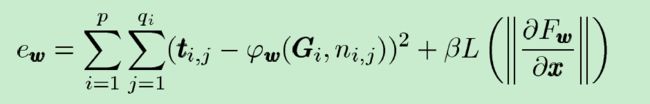
其中,如果 y > μ y > \mu y>μ,惩罚项 L ( y ) = ( y − μ ) 2 L(y) = (y-\mu)^2 L(y)=(y−μ)2,否则 L ( y ) = 0 L(y) = 0 L(y)=0,所有取值范围是 ( 0 , 1 ) (0,1) (0,1)之间的 μ \mu μ定义了 F w F_w Fw的压缩常数。更广泛的,惩罚项可以是对 w w w可微,对Jacobian范数单调递增的任意形式。例如,本文使用了 p w = ∑ i = 1 s L ( ∣ ∣ A i ∣ ∣ 1 ) p_w=\sum_{i=1}^{s}{L(||A^i||_1)} pw=∑i=1sL(∣∣Ai∣∣1)的惩罚,其中, A i A^i Ai是 ∂ F w / ∂ x \partial{F_w}/ \partial{x} ∂Fw/∂x的第i列。事实上,这样的表示是 L ( ∣ ∣ ∂ F w / ∂ x ∣ ∣ 1 ) = L ( m a x ∣ ∣ A i ∣ ∣ 1 ) L(||\partial{F_w}/ \partial{x}||_1)={L(max||A^i||_1)} L(∣∣∂Fw/∂x∣∣1)=L(max∣∣Ai∣∣1)的一个近似。
E.和Random Walks及RNN的比较
GNN被证实是其他模型的扩展。
1.RNN是GNN的一个特例,因为:
- 输入图是有向无环图
- f w f_w fw的输入限于 l n l_n ln和 x c h [ n ] x_{ch[n]} xch[n], c h [ n ] ch[n] ch[n]是结点 n n n的孩子节点的集合。
- 有supersource节点sn,可以通过该节点抵达任何其他的结点。该节点通常用作输出 o s n o_{sn} osn(graph-focused任务)。
2.GNN也涵盖了Random Walks的特点。此时 f w f_w fw是线性函数。

公式(15)中, p a [ n ] pa[n] pa[n]表示节点 n n n的父节点, a n , i ≥ 0 a_{n,i}\geq 0 an,i≥0,且是实数,对任意的 n n n, i i i都成立。 a n , i a_{n,i} an,i是经过归一化的,即 ∑ i ∈ p a [ n ] a n , i = 1 \sum_{i\in{pa[n]}}a_{n,i}=1 ∑i∈pa[n]an,i=1。事实上,公式(15)可以表示在图上的随机探索, a n , i a_{n,i} an,i表示探测器经过节点 n n n,决定走到节点 i i i的概率。状态 x n x_n xn表示探测器在节点 n n n上处于就绪状态的概率。当所有的 x n x_n xn被堆进向量 x x x时,公式(15)变为 x = A x x=Ax x=Ax, A = { a n , i } A=\{a_{n,i}\} A={an,i},当 i ∉ p a [ n ] i\notin pa[n] i∈/pa[n]时, a n , i = 0 a_{n,i} = 0 an,i=0。很容易证明, ∣ ∣ A ∣ ∣ 1 = 1 ||A||_1=1 ∣∣A∣∣1=1。马尔科夫链暗示如果存在t,使矩阵 A t A^t At的所有元素非空(nonnull),那么公式(15)就是压缩映射。因此,在上述A的条件成立时,图上的随机探索是GNN的一个实例,其中 A A A是一个恒定的随机矩阵,而不是由神经网络生成。
后续内容是计算代价分析、实验和结论,本文不做详述。本文只对方法和思想详述,具体内容参考原文。