数据分析：个人贷款违约案例（逻辑回归）

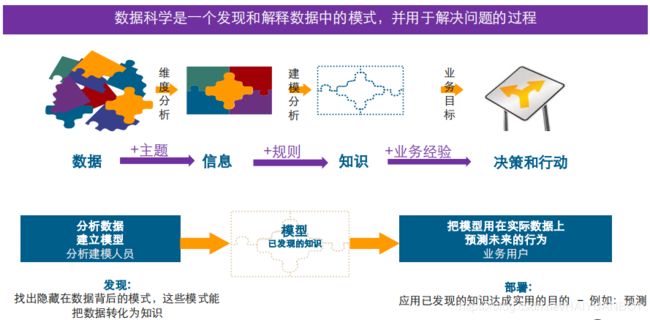
数据科学方法论

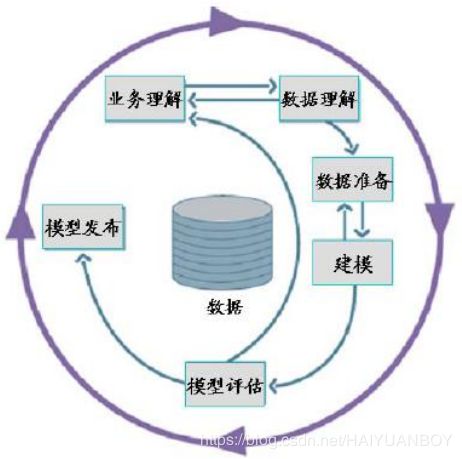
数据挖掘实施路线图

案例背景

• 本数据为一家银行的个人金融业务数据集，可以作为银行场景下进行个人客户业务分析和数据挖掘的示例。这份数据中涉及到5300个银行客户的100万笔的交易，而且涉及700份贷款信息与近900张信用卡的数据。通过分析这份数据可以获取与银行服务相关的业务知识。例如，提供增值服务的银行客户经理，希望明确哪些客户有更多的业务需求，而风险管理的业务人员可以及早发现贷款的潜在损失
• 可否根据客户贷款前的属性、状态信息和交易行为预测其贷款违约行为
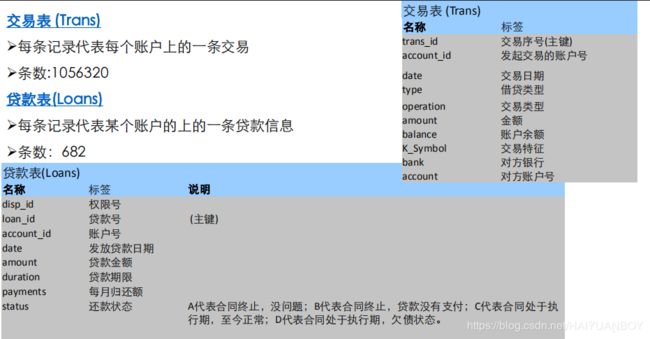
• 截取自一家银行的真实客户与交易数据
• 涉及客户主记录、帐号、交易、业务和信用卡数据
• 一个账户只能一笔贷款，“loan” 表中记录了客户贷款信息

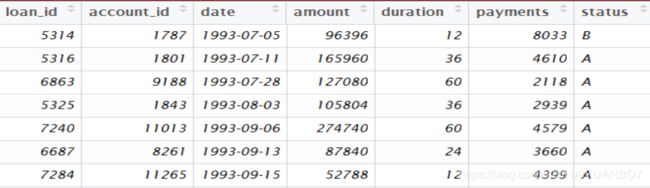
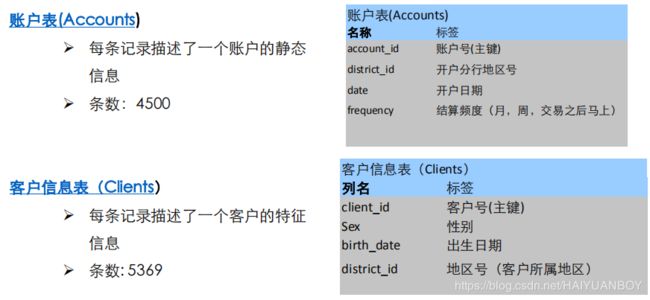
数据表 

根据以往的贷款数据，状态为B和D的为违约客户，A为正常客户，C的最终状态还不明确 

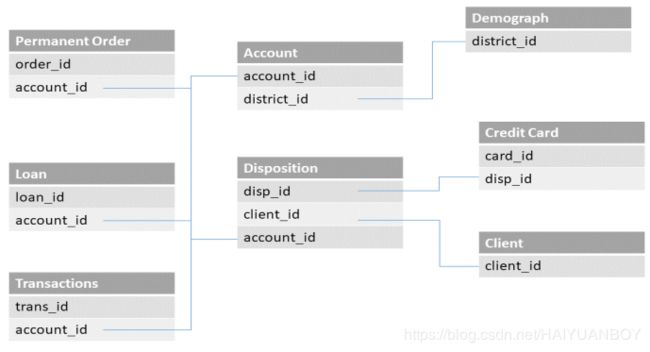
表的关系：数据的实体-关系图(ER图)

业务理解

思路整理

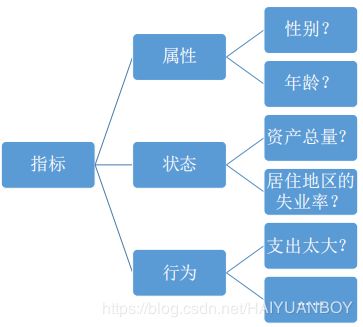
什么指标有预测能力？

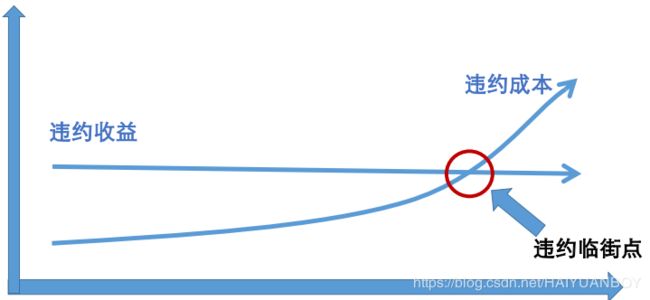
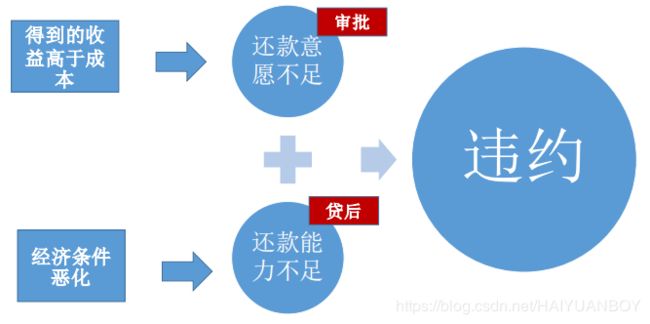
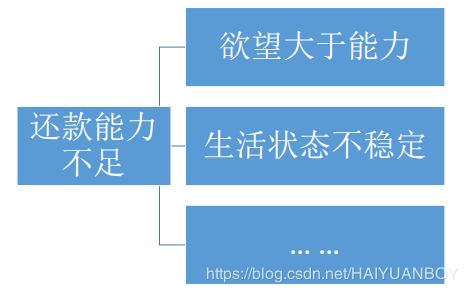
客户为什么不还钱？

有预测价值的变量基本都是衍生变量：

• 一级衍生，比如资产余额
• 二级衍生，比如资产余额的波动率、平均资产余额
• 三级衍生，比如资产余额的变异系数

数据提取

• 相关与因果之间的关系
• 注意构建模型时数据选取的标准

不是所有具有相关关系的数据都能拿来建模，要注意搞清楚因果关系，如上世纪80年代，姚明鞋的尺寸和GDP总量明显正相关，但它们没有因果关系

建立因果关系模型

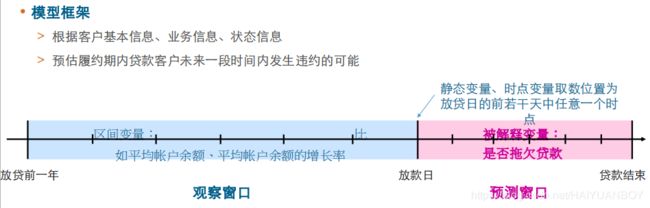
• 我们分析的变量按照时间变化情况可以分为动态变量和静态变量
• 属性变量（比如性别、是否90后）一般是静态变量，行为、状态和利益变量均属于动态变量
• 动态变量还分为时点变量和区间变量，状态变量（比如当前帐户余额、是否破产）和利益变量（对某产品的诉求）均属于时点变量。行为变量（存款频次、平均帐户余额的增长率）为区间变量

贷款违约预测的取数规则

数据处理代码

# In[ ]:

import pandas as pd
import os

# # 1 数据整理

# ## 1.1导入数据

# In[2]: 读入 csv 文件
os.chdir("D:\pydata\案例")
loanfile = os.listdir()
createVar = locals()
for i in loanfile:
    if i.endswith("csv"):        
        createVar[i.split('.')[0]] = pd.read_csv(i, encoding = 'gbk')
        print(i.split('.')[0])


# ## 1.2、生成被解释变量bad_good

# In[3]:

bad_good = {'B':1, 'D':1, 'A':0, 'C': 2}
loans['bad_good'] = loans.status.map(bad_good)
loans.head()


Out[3]: 
   loan_id  account_id        date    ...     payments  status  bad_good
0     5314        1787  1993-07-05    ...         8033       B         1
1     5316        1801  1993-07-11    ...         4610       A         0
2     6863        9188  1993-07-28    ...         2118       A         0
3     5325        1843  1993-08-03    ...         2939       A         0
4     7240       11013  1993-09-06    ...         4579       A         0


# ## 1.3、借款人的年龄、性别

# In[4]: 左连接

data2 = pd.merge(loans, disp, on = 'account_id', how = 'left')
data2 = pd.merge(data2, clients, on = 'client_id', how = 'left')
data2=data2[data2.type=='所有者']

data2.head()


Out[4]: 
   loan_id  account_id        date     ...       sex  birth_date  district_id
0     5314        1787  1993-07-05     ...         女  1947-07-22           30
1     5316        1801  1993-07-11     ...         男  1968-07-22           46
2     6863        9188  1993-07-28     ...         男  1936-06-02           45
3     5325        1843  1993-08-03     ...         女  1940-04-20           14
4     7240       11013  1993-09-06     ...         男  1978-09-07           63


# ## 1.4、借款人居住地的经济状况
# In[5]: district 表中的 district_id 为 A1 这一列

data3 = pd.merge(data2, district, left_on = 'district_id', right_on = 'A1', how = 'left')
data3.head()


Out[5]: 
   loan_id  account_id        date  amount  ...    A13  A14   A15   a16
0     5314        1787  1993-07-05   96396  ...   3.67  100  15.7  14.8
1     5316        1801  1993-07-11  165960  ...   2.31  117  12.7  11.6
2     6863        9188  1993-07-28  127080  ...   2.89  132  13.3  13.6
3     5325        1843  1993-08-03  105804  ...   1.71  135  18.6  17.7
4     7240       11013  1993-09-06  274740  ...   4.52  110   9.0   8.4


# ## 1.5、贷款前一年内的账户平均余额、余额的标准差、变异系数、平均收入和平均支出的比例

# In[6]: amount 属于 trans 表的

data_4temp1 = pd.merge(loans[['account_id', 'date']],
                       trans[['account_id','type','amount','balance','date']],
                       on = 'account_id')
# 重新指定列名
data_4temp1.columns = ['account_id', 'date', 'type', 'amount', 'balance', 't_date']

data_4temp1 = data_4temp1.sort_values(by = ['account_id','t_date'])

data_4temp1['date']=pd.to_datetime(data_4temp1['date'])
data_4temp1['t_date']=pd.to_datetime(data_4temp1['t_date'])
data_4temp1.tail()


Out[6]: 
        account_id       date type  amount balance     t_date
127263       11362 1996-12-27    借     $56  $51420 1998-12-08
127264       11362 1996-12-27    借  $4,780  $46640 1998-12-10
127265       11362 1996-12-27    借  $5,392  $41248 1998-12-12
127266       11362 1996-12-27    借  $2,880  $38368 1998-12-19
127267       11362 1996-12-27    贷    $163  $38531 1998-12-31


# ## 将对账户余额进行清洗
# In[9]:

data_4temp1['balance2'] = data_4temp1['balance'].map(
    lambda x: int(''.join(x[1:].split(','))))
data_4temp1['amount2'] = data_4temp1['amount'].map(
    lambda x: int(''.join(x[1:].split(','))))

data_4temp1.head()


Out[7]: 
       account_id       date type   ...       t_date balance2 amount2
10020           2 1994-01-05    贷   ...   1993-02-26     1100    1100
10021           2 1994-01-05    贷   ...   1993-03-12    21336   20236
10022           2 1994-01-05    贷   ...   1993-03-28    25036    3700
10023           2 1994-01-05    贷   ...   1993-03-31    25050      14
10024           2 1994-01-05    贷   ...   1993-04-12    45286   20236


# ## 根据取数窗口提取交易数据
# In[10]: 取贷款时间和上一次交易时间相隔一年的记录

import datetime
data_4temp2 = data_4temp1[data_4temp1.date>data_4temp1.t_date][
    data_4temp1.date

模型构建与评估

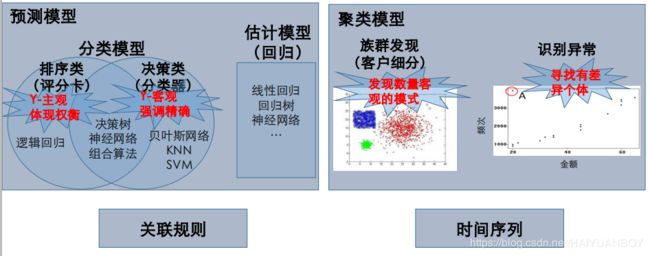
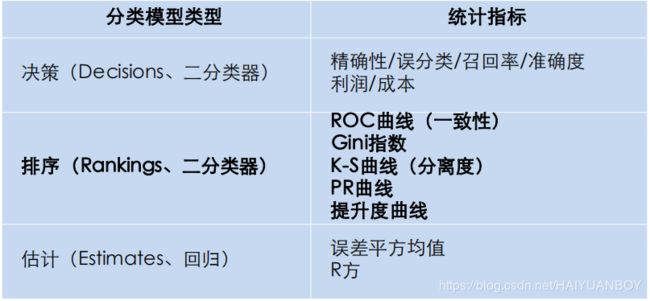
数据挖掘模型分类

此案列中，我们的信用评估是主观定义的，排序类模型反应一个人成本与收益的决策行为，而决策类模型反应的是真实情况的

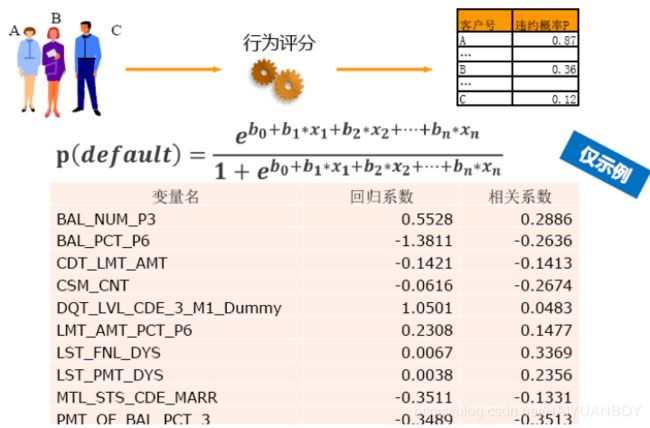
使用逻辑回归建立行为评分卡

逻辑回归预测的是一个人违约的概率，然后以概率从大到小进行排序，概率大的拒绝，概率小的接受

评估指标汇总

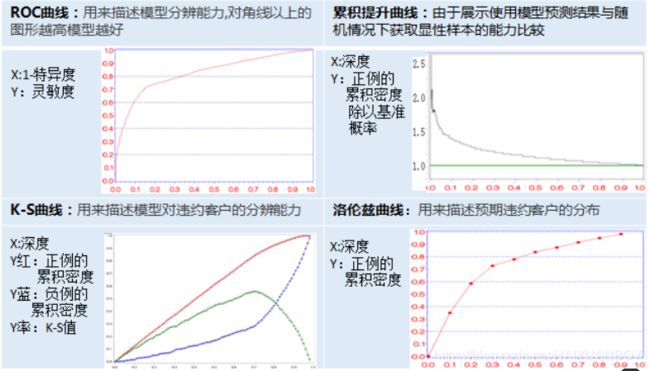
对评分卡模型，我们更多用 ROC 曲线和 K-S 曲线，ROC 曲线越偏向左上角及围的右下方面积越大模型表现越好，K-S曲线红蓝线越分离模型表现越好，绿线代表两条曲线的差值，值越大模型表现越好

评分卡模型的评估指标

建模与评测代码

训练

# In[17]:
# status 为 C 的记录不用来训练，而作为预测用
data_model=data4[data4.status!='C']
for_predict=data4[data4.status=='C']
#%%
train = data_model.sample(frac=0.7, random_state=1235).copy()
# 剩下的 30% 的样本
test = data_model[~ data_model.index.isin(train.index)].copy()
print(' 训练集样本量: %i \n 测试集样本量: %i' %(len(train), len(test)))


 训练集样本量: 195 
 测试集样本量: 84

#%%
# 有一种说法是当训练集每一个类别数量都相等时，会提高模型性能，下面注释代码调整 3 中类别数量一致，但在这准确度反而下降了
'''
train_D = train[train['status']=='D']
train_D_1 = train_D[train['account_id']==3189]
for i in range(4):
    train = pd.concat([train, train_D])
for i in range(5):
    train = pd.concat([train, train_D_1])
train_B = train[train['status']=='B']
train_B_1 = train[train['account_id']==19]
for i in range(5):
    train = pd.concat([train, train_B])
for i in range(13):
    train = pd.concat([train, train_B_1])
print(' 训练集样本量: %i \n 测试集样本量: %i' %(len(train), len(test)))

train['status'].value_counts()
'''


# In[22]:

# 向前法
def forward_select(data, response):
    import statsmodels.api as sm
    import statsmodels.formula.api as smf
    remaining = set(data.columns)
    remaining.remove(response)
    selected = []
    current_score, best_new_score = float('inf'), float('inf')
    while remaining:
        aic_with_candidates=[]
        for candidate in remaining:
            formula = "{} ~ {}".format(
                response,' + '.join(selected + [candidate]))
            aic = smf.glm(
                formula=formula, data=data, 
                family=sm.families.Binomial(sm.families.links.logit)
            ).fit().aic
            aic_with_candidates.append((aic, candidate))
        aic_with_candidates.sort(reverse=True)
        best_new_score, best_candidate=aic_with_candidates.pop()
        if current_score > best_new_score: 
            remaining.remove(best_candidate)
            selected.append(best_candidate)
            current_score = best_new_score
            print ('aic is {},continuing!'.format(current_score))
        else:        
            print ('forward selection over!')
            break
            
    formula = "{} ~ {} ".format(response,' + '.join(selected))
    print('final formula is {}'.format(formula))
    model = smf.glm(
        formula=formula, data=data, 
        family=sm.families.Binomial(sm.families.links.logit)
    ).fit()
    return(model)


# In[23]:

candidates = ['bad_good', 'A1', 'GDP', 'A4', 'A10', 'A11', 'A12','amount', 'duration',
       'A13', 'A14', 'A15', 'a16', 'avg_balance', 'stdev_balance',
       'cv_balance', 'income', 'out', 'r_out_in', 'r_lb', 'r_lincome']
data_for_select = train[candidates]

lg_m1 = forward_select(data=data_for_select, response='bad_good')
lg_m1.summary().tables[1]


aic is 167.43311432504638,continuing!
aic is 135.8243585604184,continuing!
forward selection over!
final formula is bad_good ~ r_lb + cv_balance 

# 最后选出两个变量 r_lb 和 cv_balance 对模型结果影响最大，r_lb 反应客户的对钱的欲望，cv_balance 反应客户经济的不稳定性

预测

import sklearn.metrics as metrics
import matplotlib.pyplot as plt
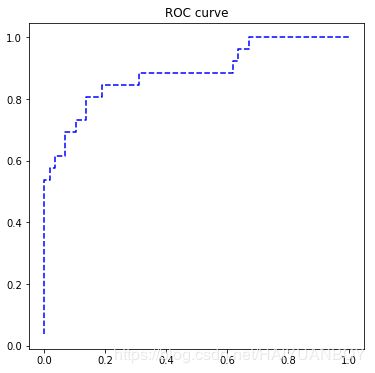
fpr, tpr, th = metrics.roc_curve(test.bad_good, lg_m1.predict(test))
plt.figure(figsize=[6, 6])
plt.plot(fpr, tpr, 'b--')
plt.title('ROC curve')
plt.show()

# In[25]:

print('AUC = %.4f' %metrics.auc(fpr, tpr))


AUC = 0.8846

# In[28]:

for_predict['prob']=lg_m1.predict(for_predict)
for_predict[['account_id','prob']].head()


Out[22]: 
    account_id      prob
23        1071  0.704914
30        5313  0.852249
38       10079  0.118128
39        5385  0.177591
42        8321  0.024302